Chapter 4 Determinants and Matrices Ex 4.4
Chapter 4 Determinants and Matrices Ex 4.4
Question 1.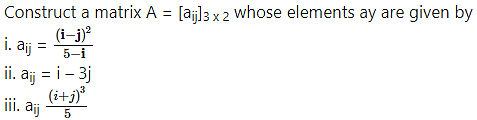
Solution:
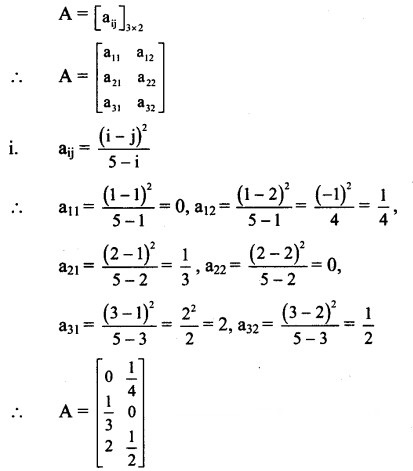

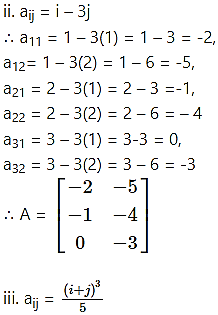
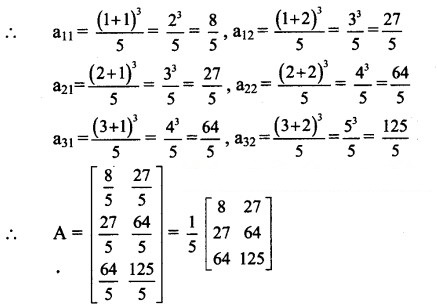
Question 2.
Classify the following matrices as a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew- symmetric matrix.

As every element below the diagonal is zero in matrix A.
∴ A is an upper triangular matrix.

∴ A is a skew-symmetric matrix.

As matrix A has only one row.
∴ A is a row matrix.

As matrix A has all its non-diagonal elements zero and diagonal elements same.
∴ A is a scalar matrix.

As every element above the diagonal is zero in matrix A.
∴ A is a lower triangular matrix.
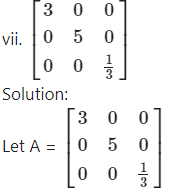
As matrix A has all its non-diagonal elements zero.
∴ A is a diagonal matrix.
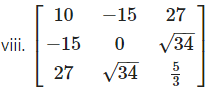
Solution:

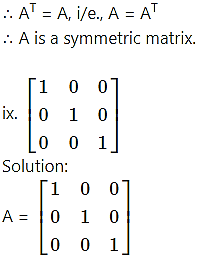
In matrix A, all the non-diagonal elements are zero and diagonal elements are one.
∴ A is a unit (identity) matrix.

∴ A is a symmetric matrix.
∴ A is a symmetric matrix.
Question 3.
Which of the following matrices are singular or non-singular?
Solution:


= 3(5 – 8) – 5(-10 – 12) + 7(-4 – 3)
= -9 + 110 – 49 = 52 ≠ 0
∴ A is a non-singular matrix.
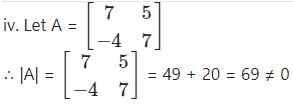
Question 4.
Find k, if the following matrices are singular.

∴ 4(k – 9) – 3(7 – 10) + 1(63 – 10k) = 0
∴ 4k – 36 + 9 + 63 – 10k = 0
∴ -6k + 36 = 0
∴ 6k = 36
∴ k = 6
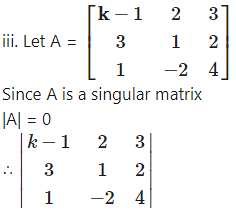
∴ (k – 1)(4 + 4) – 2(12 – 2) + 3 (-6 – 1) = 0
∴ 8k-8-20-21 =0
∴ 8k = 49
∴ k = 49/8
Question 5.
Solution: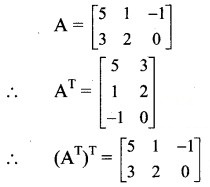
Question 6.
If A =, find (.
Solution:

Question 7.
Solution:

Question 8.
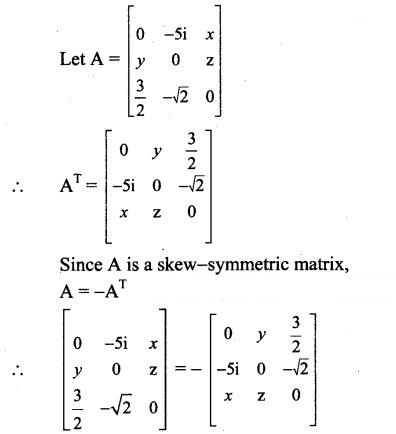
Find x, y, z, if is a symmetric matrix.
Solution:
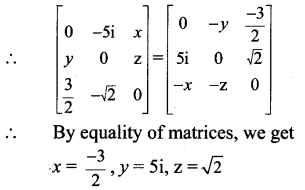
Question 9.
For each of the following matrices, using its transpose, state whether it is symmetric, skew-symmetric or neither.
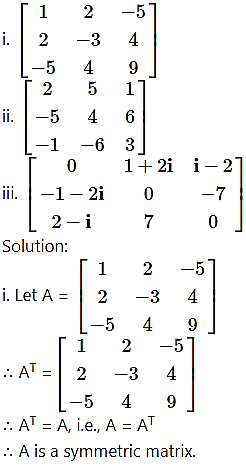
ii.

![]()
∴ A is neither a symmetric nor skew-symmetric matrix.
iii.
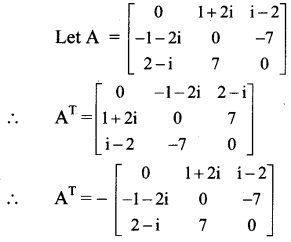
∴ = -A, i.e., A = –
∴ A is a skew-symmetric matrix.
Question 10.

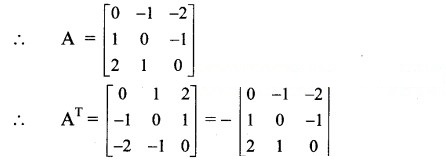
∴ = -A, i.e., A = –
∴ A is a skew-symmetric matrix.