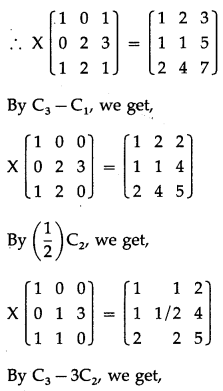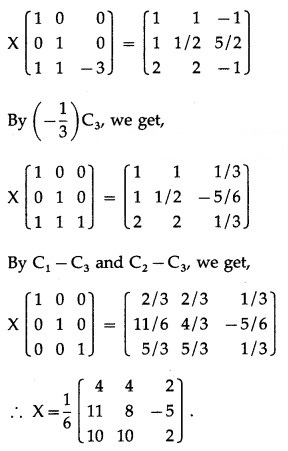Blog

Chapter 2 Matrices Miscellaneous Exercise 2A

Chapter 2 Matrices Miscellaneous Exercise 2A

Question 1.

Question 2.

By R₁ – R₂, we get,

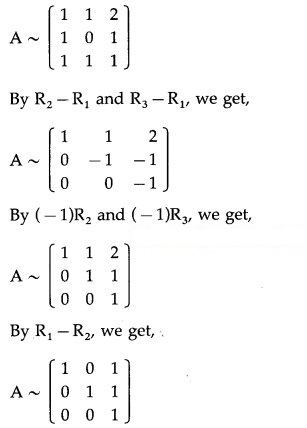
By R₁ – R₃ and By R₂ – R₃, we get

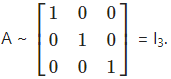
Question 3.
Check whether the following matrices are invertible or not:

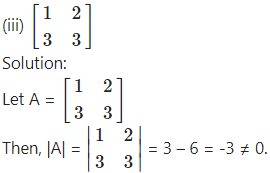
∴ A is a non-singular matrix.
Hence, A^-1 exist.

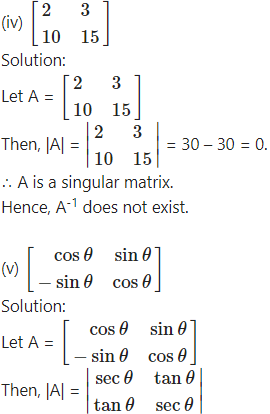
= sec²θ – tan²θ = 1 ≠ 0.
∴ A is a non-singular matrix.
Hence, A^-1 exist.

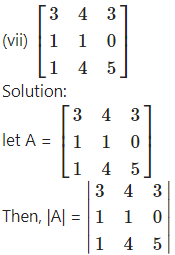
= 3(5 – 0) – 4(5 – 0) + 3(4 – 1)
= 15 – 20 + 9 = 4 ≠ 0
∴ A is a non-singular matrix.
Hence, A^-1 exist.

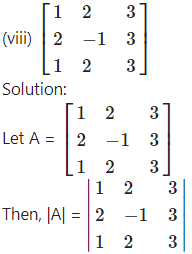
= 1 (-3 -6) – 2 (6 – 3) + 3 (4 + 1)
= -9 – 6 + 15 = 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

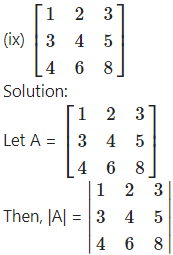
= 1(32 – 30) – 2(24 – 20) + 3(18 – 16)
= 2 – 8 + 6 = 0
∴ A is a singular matrix.
Hence, A^-1 does not exist.

Question 4.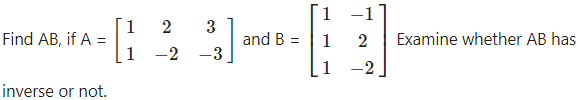

Solution:

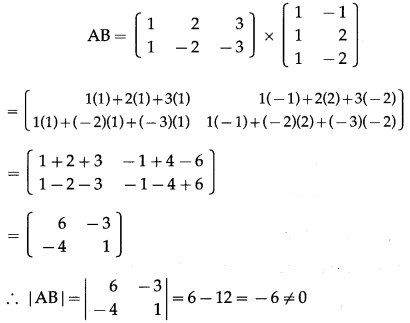
∴ A is a non-singular matrix.
Hence, (AB)^-1 exist.

Question 5.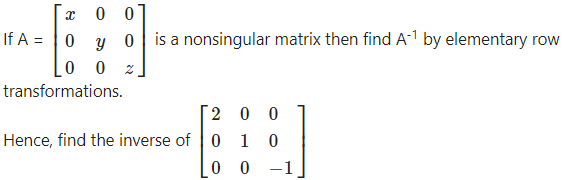

Solution:
Since A is a non-singular matrix, then find A^-1 by using elementary row transformations.
We write AA^-1 = I

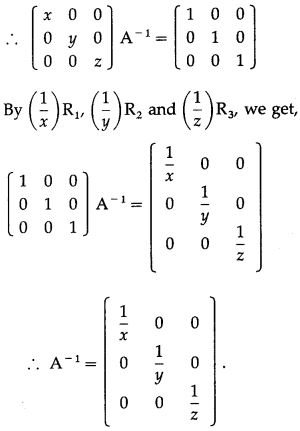
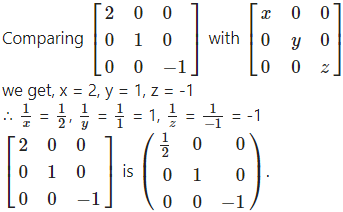
Question 6.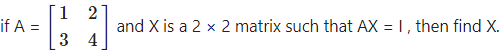

Solution:
We will reduce the matrix A to the identity matrix by using row transformations. During this pro¬cess, I will be converted to the matrix X.
We have AX = I.

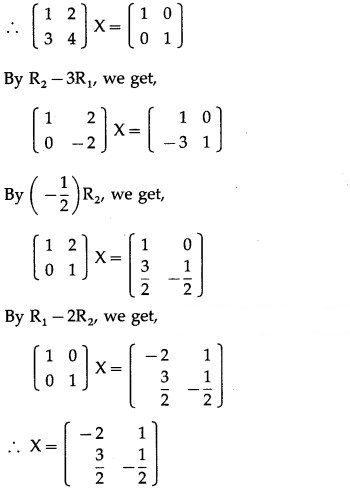
Question 7.
Find the inverse of each of the following matrices (if they exist).

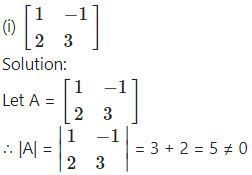
∴ A^-1 exists.
Consider AA^-1 = I

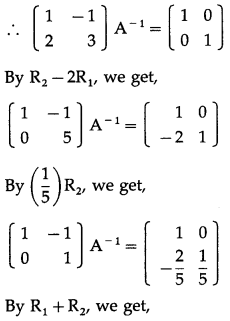
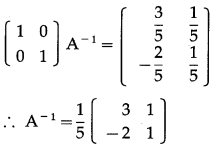
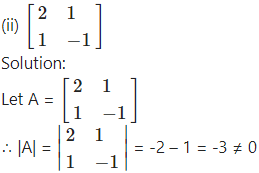
∴ A^-1 exists.
Consider AA^-1 = I

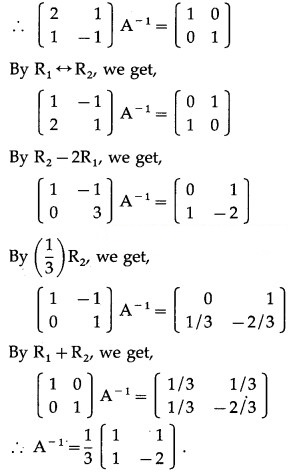
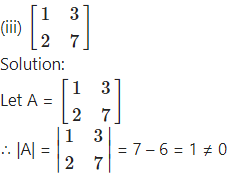
∴ A^-1 exists.
Consider AA^-1 = I

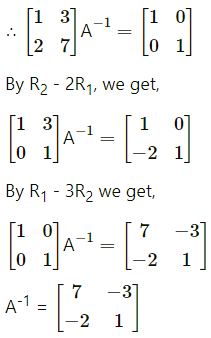
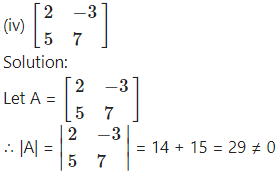
∴ A^-1 exists.
Consider AA^-1 = I

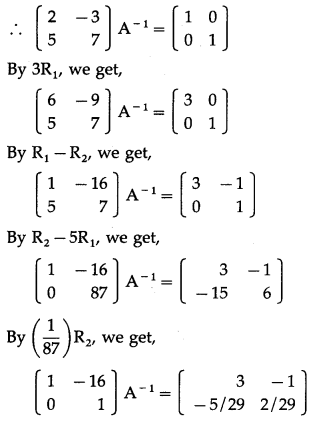
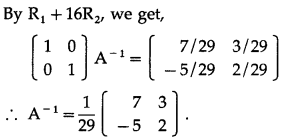
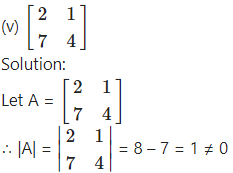
∴ A^-1 exists.
Consider AA^-1 = I

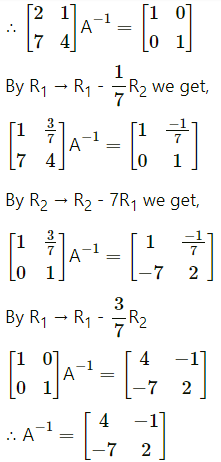
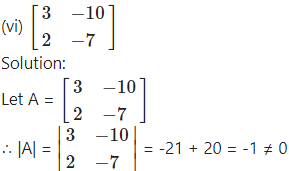
∴ A^-1 exists.
Consider AA^-1 = I

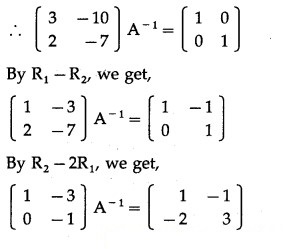
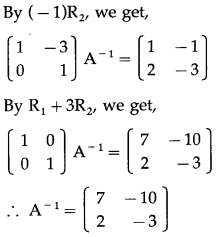
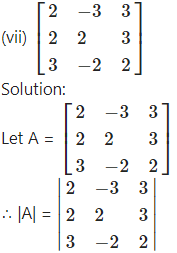
= 2(4 + 6) +3(4 – 9) + 3(-4 – 6)
= 20 – 15 – 30 = -25 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

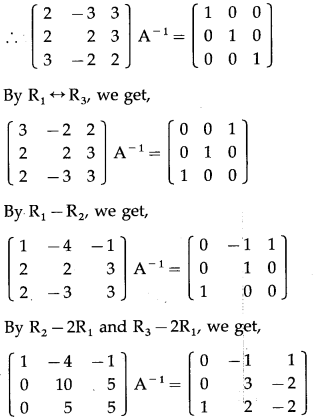
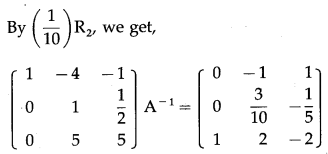
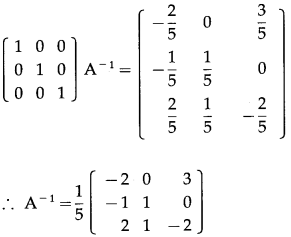
= 1(0 + 25) + 3(0 + 10) + 2(-15 – 0)
= 25 + 30 -30
= 25 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

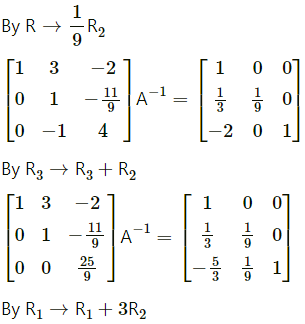
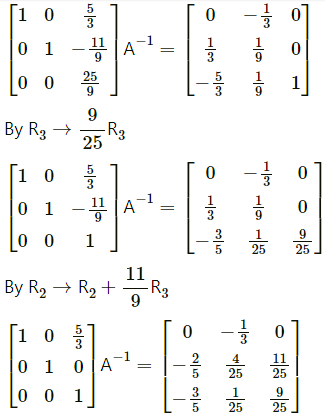
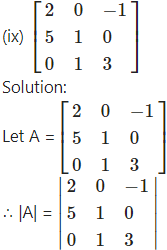
= 2(3 – 0) – 0 – 1(5 – 0)
= 6 – 0 – 5 = 1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

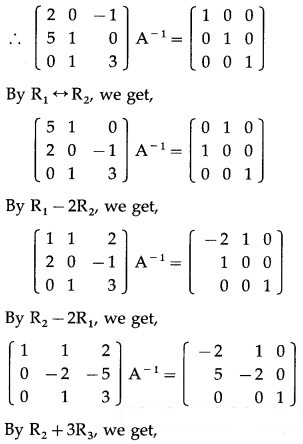
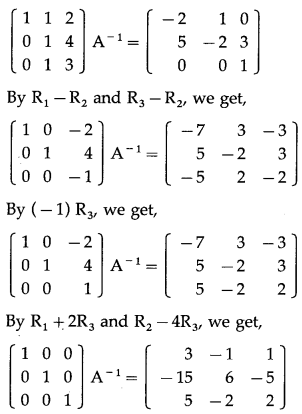
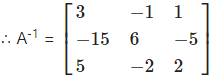
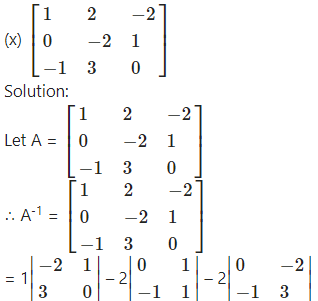
|A| = 1(0 – 3) – 2(0 + 1) – 2(0 – 2)
= -3 – 2 + 4
= -1 ≠ 0
∴ A^-1 exists.
We have
AA^-1 = I

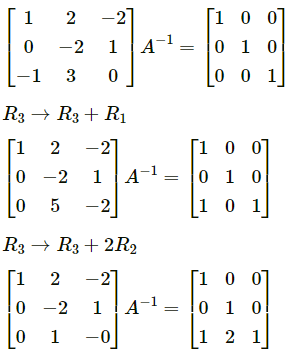
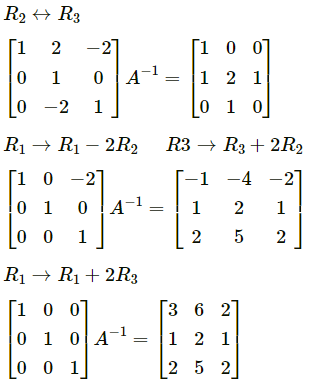
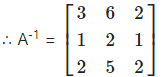
Question 8.

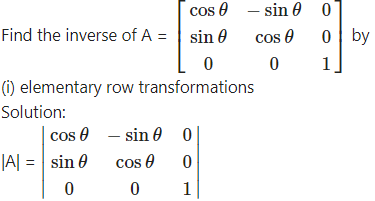
= cosθ (cosθ – 0) + sinθ (sinθ – 0) + 0
= cos²θ + sin²θ = 1 ≠ 0
∴ A^-1 exists.
(i) Consider AA^-1 = I

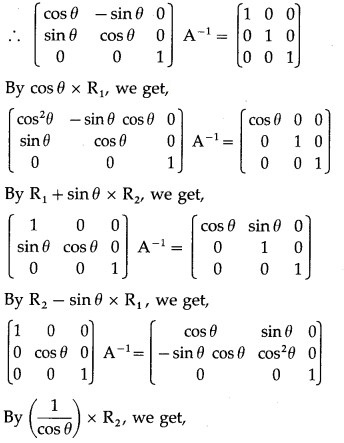
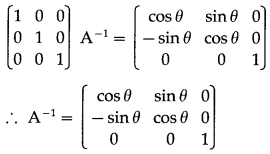
(ii) elementary column transformations
Solution:
Consider A^-1A = I

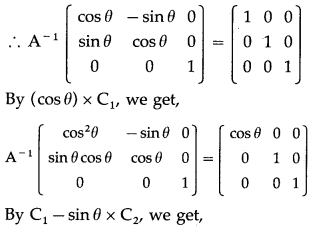
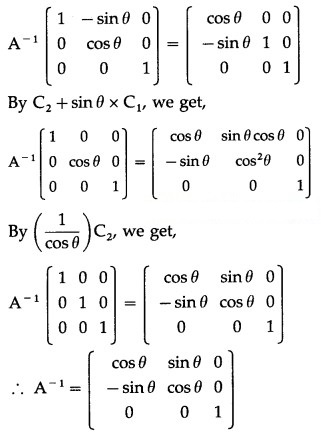
Question 9.





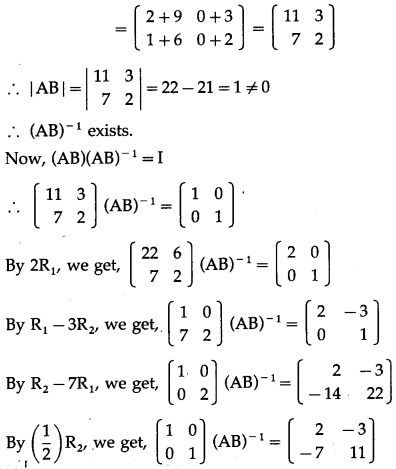
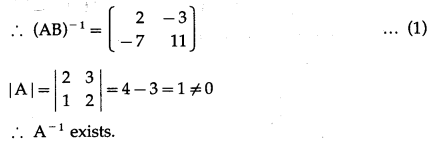
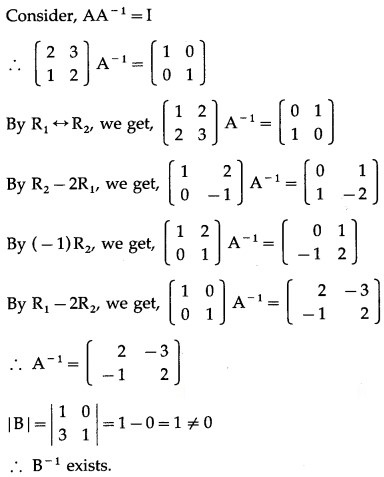
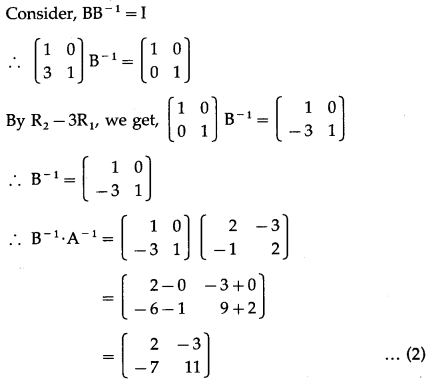
From (1) and (2), (AB)^-1 = B^-1 ∙ A^-1.

Question 10.

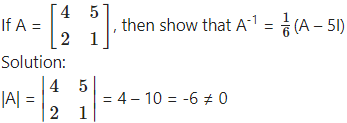
∴ A^-1 exists.
Consider AA^-1 = I

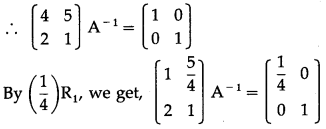
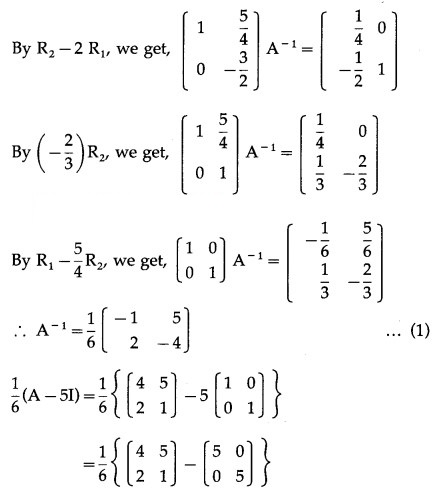
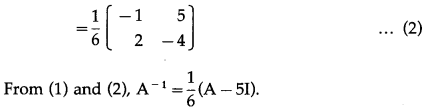
Question 11.

Solution:
AX = B

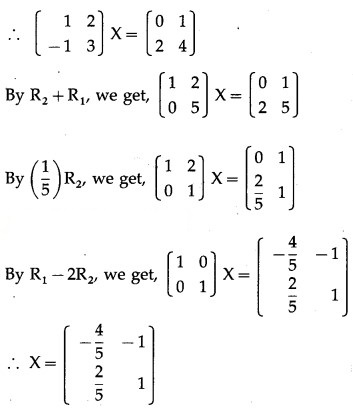
Question 12.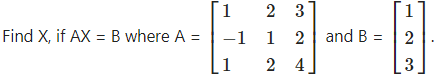

Solution:
AX = B

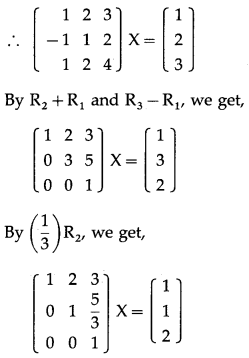
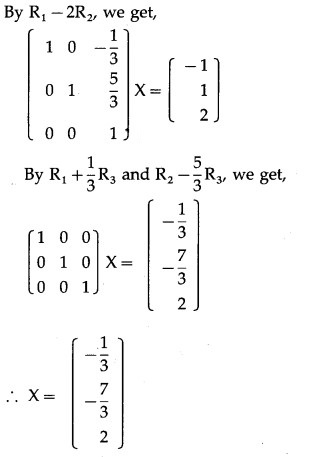
Question 13.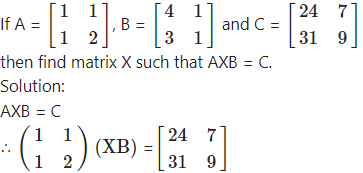

First we perform the row transformations.

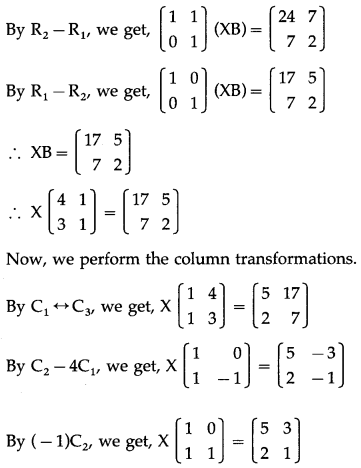
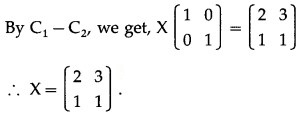
Question 14.

= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A^-1 exists.
First we have to find the cofactor matrix

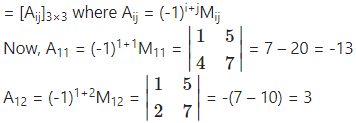
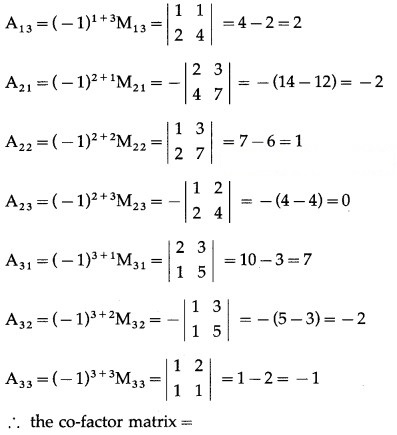
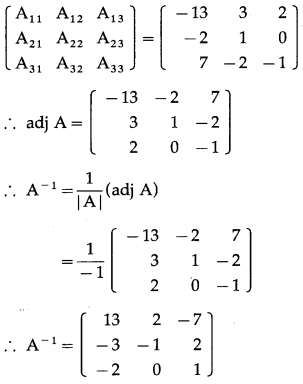
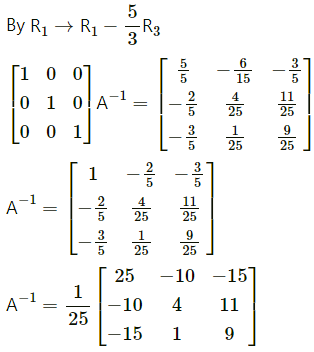
Question 15.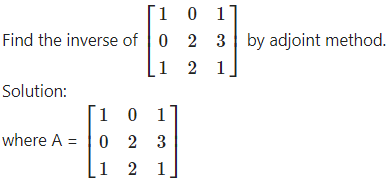

|A| = 1(2 – 6) – 0(0 – 3) + 1(0 – 2)
|A| = -4 – 2
|A| = -6 ≠ 0
∴ A^-1 exists.
First we have to find the cofactor matrix
= [A_ij]3×3, where A_ij = (-1)^i+jM_ij

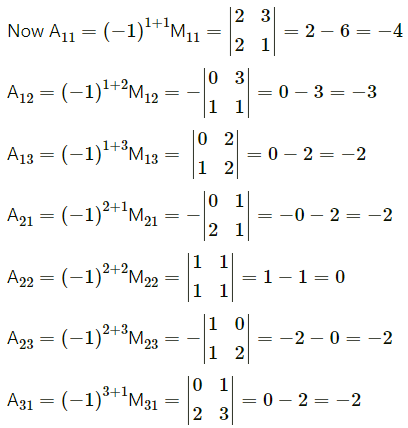
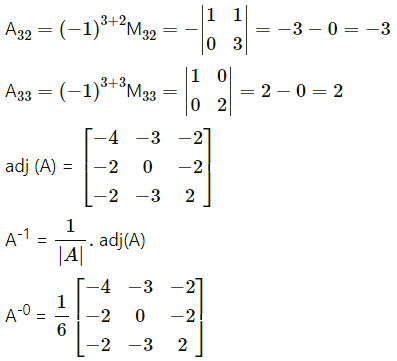
Question 16.

= 1(4 – 4) – 2(-4 – 2) + 3(-2 – 1)
= 0 + 12 – 9 = 3 ≠ 0
∴ A^-1 exists.
A^-1by adjoint method :
We have to find the cofactor matrix
= [A_ij]_3×3, where A_ij = (-1)^i+j M_ij

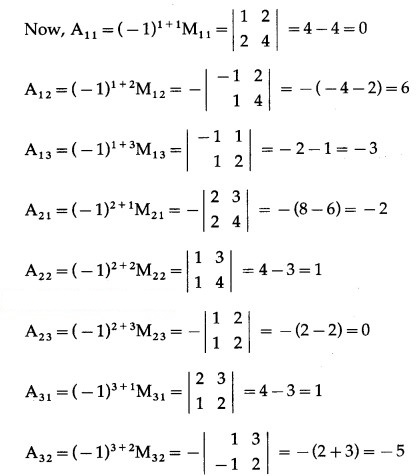
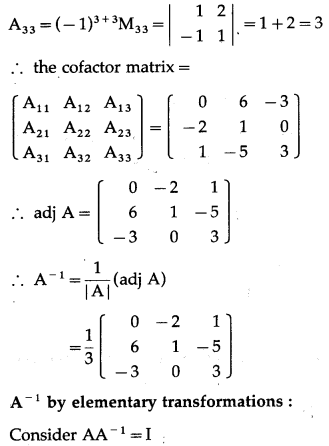
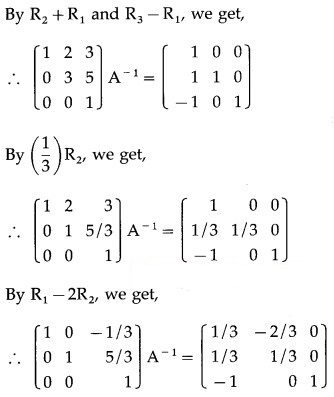
Question 17.

= 1 (2 – 6) – 0 + 1 (0 – 2)
= -4 – 2= -6 ≠ 0
∴ A^-1 exists.
Consider A^-1A = I

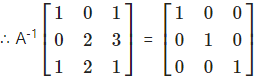
By C₃ – C₁, we get,

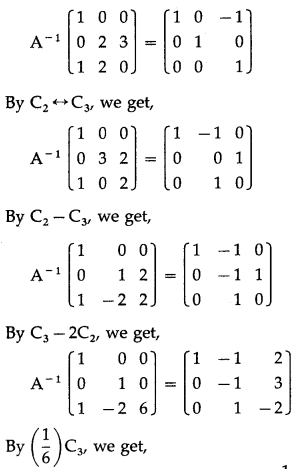
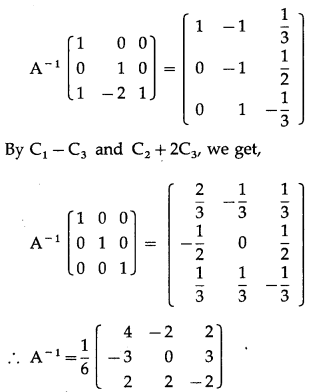
Question 18.

= 1(7 – 20) – 2(7 – 10) + 3(4 – 2)
= -13 + 6 + 6 = -1 ≠ 0
∴ A^-1 exists.
Consider AA^-1 = I

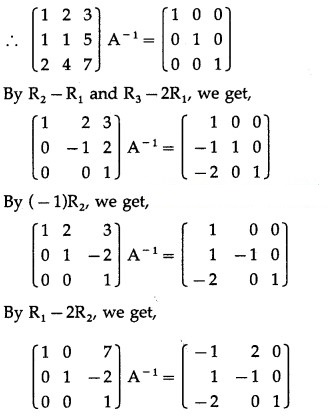
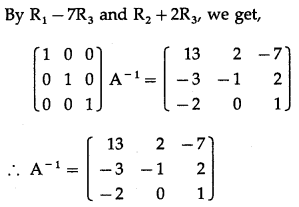
Question 19.
Show with usual notations that for any matrix A = [a_ij]_3×3
(i) a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃ = 0
Solution:

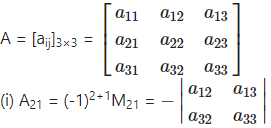
= -(a₁₂a₃₃ – a₁₃a₃₂)
= -a₁₂a₃₃ + a₁₃a₃₂

= a₁₁a₃₃ – a₁₃a₃₁

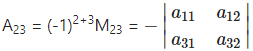
= -(a₁₁a₃₂ – a₁₂a₃₁)
= -a₁₁a₃₂+ a₁₂a₃₁
∴ a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃
= a₁₁(-a₁₂₃₃ + a₁₃a₃₂) + a₁₂(a₁₁a₃₃ – a₁₃a₃₁) + a₁₃(-a₁₁a₃₂ + a₁₂a₃₁)
= -a₁₁a₁₂a₃₃ + a₁₁a₁₃a₃₂ + a₁₁a₁₂a₃₃ – a₁₂a₁₃a₃₁ – a₁₁a₁₃a₃₂ + a₁₂a₁₃a₃₁
= 0

(ii) a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ = |A|
Solution:

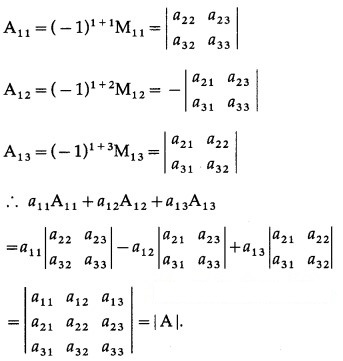
Question 20.

Solution:
Consider XA = B