Blog

Chapter 6 Line and Plane Ex 6.3

Chapter 6 Line and Plane Ex 6.3

Question 1.

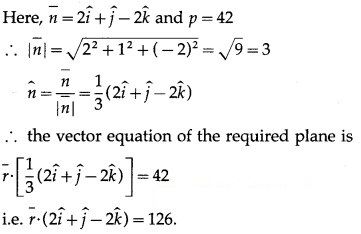
Question 2.
Find the perpendicular distance of the origin from the plane 6x – 2y + 3z – 7 = 0.
Solution:



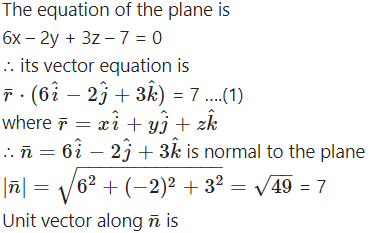
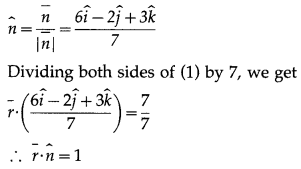
Alternative Method:
The equation of the plane is 6x – 2y + 3z – 7 = 0 i.e. 6x – 2y + 3z = 7

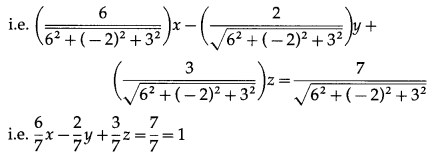
This is the normal form of the equation of plane.
∴ perpendicular distance of the origin from the plane is p = 1 unit.

Question 3.
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x + 6y – 3z = 63 .
Solution:

Question 4.

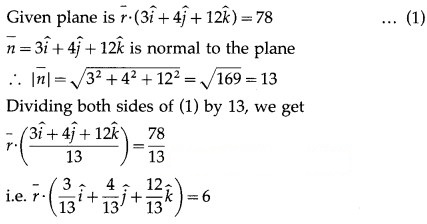
Question 5.

Question 6.
Find the Cartesian equation of the plane passing through A( -1, 2, 3), the direction ratios of whose normal are 0, 2, 5.
Solution:
The cartesian equation of the plane passing ; through (x₁, y₁, z₁), the direction ratios of whose normal are a, b, c, is
a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
∴ the cartesian equation of the required plane is
0(x +1) + 2(y – 2) + 5(z – 3) = 0
i.e. 0 + 2y – 4 + 5z – 15 = 0
i.e. 2y + 5z = 19.

Question 7.
Find the Cartesian equation of the plane passing through A(7, 8, 6) and parallel to the XY plane.
Solution:
The cartesian equation of the plane passing through (x₁, y₁, z₁), the direction ratios of whose normal are a, b, c, is
a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
The required plane is parallel to XY-plane.
∴ it is perpendicular to Z-axis i.e. Z-axis is normal to the plane. Z-axis has direction ratios 0, 0, 1.
The plane passes through (7, 8, 6).
∴ the cartesian equation of the required plane is
0(x – 7) + 0(y – 8) + 1 (z – 6) = 0
i.e. z = 6.

Question 8.
The foot of the perpendicular drawn from the origin to a plane is M(1, 0, 0). Find the vector equation of the plane.
Solution:
The vector equation of the plane passing ; through A(a¯) and perpendicular to 

M(1, 0, 0) is the foot of the perpendicular drawn from ; origin to the plane. Then the plane is passing through M : and is perpendicular to OM.

Question 9.

Question 10.



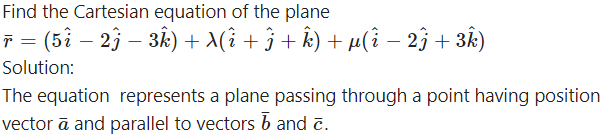
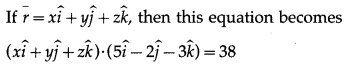
∴ 5x – 2y – 3z = 38.
This is the cartesian equation of the required plane.

Question 11.
Find the vector equation of the plane which makes intercepts 1, 1, 1 on the co-ordinates axes.
Solution:

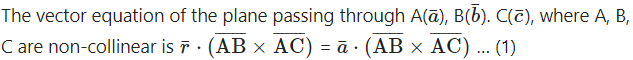
The required plane makes intercepts 1, 1, 1 on the coordinate axes.
∴ it passes through the three non-collinear points A (1, 0, 0), B = (0, 1, 0), C = (0, 0, 1)
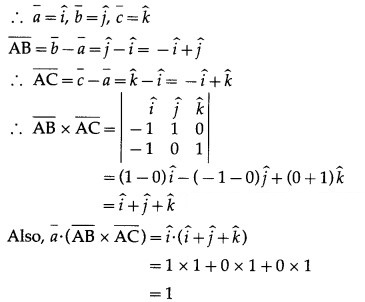