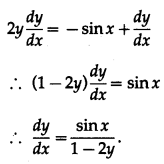Chapter 1 Differentiation Ex 1.3
Chapter 1 Differentiation Ex 1.3
Question 1.
Differentiate the following w.r.t. x:
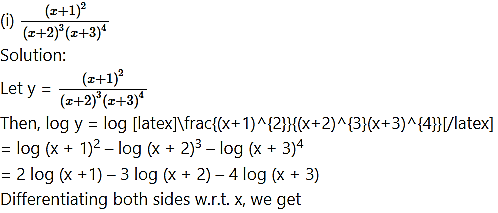

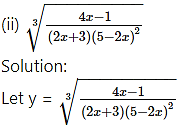
Then log y = log [latex]\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}[/latex]
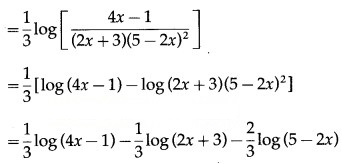
Differentiating both sides w.r.t. x, we get

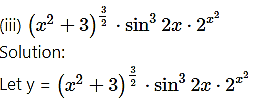
Then log y = log [latex]\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}[/latex]
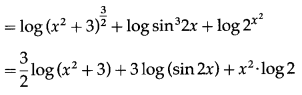
Differentiating both sides w.r.t. x, we get
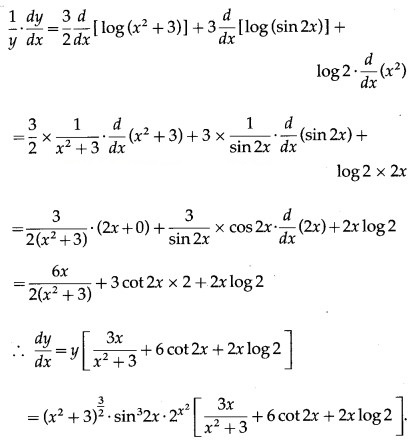
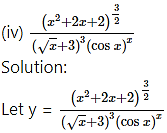
Then log y = log [latex]\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}[/latex]
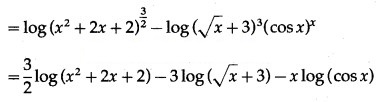
Differentiating both sides w.r.t. x, we get
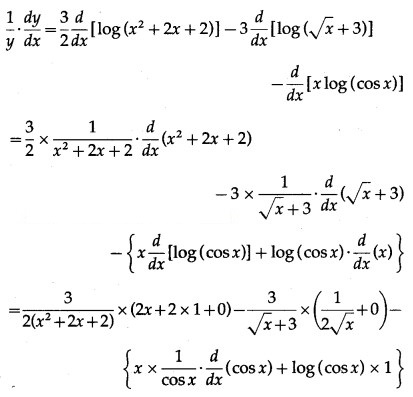
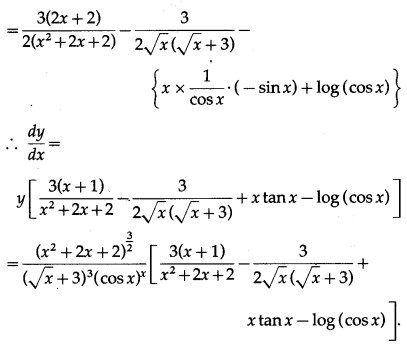
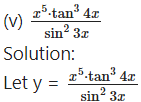
Then log y = log [latex]\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}[/latex]
= log + log ta4x – log si3x
= 5 log x+ 3 log (tan 4x) – 2 log (sin 3x)
Differentiating both sides w.r.t. x, we get
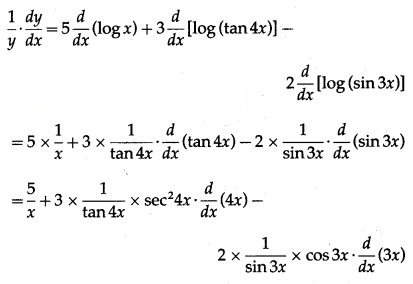
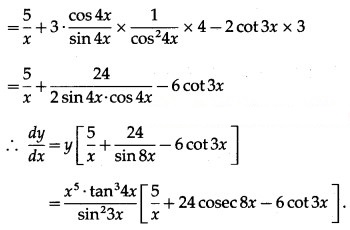
(vi)
Solution:
Let y =
Then log y = log () = ()(log x)
Differentiating both sides w.r.t. x, we get
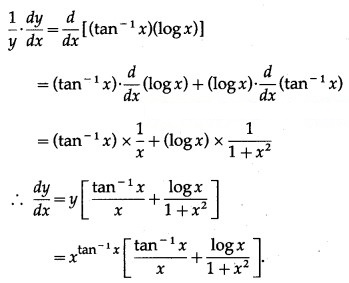
(vii) (sin x
Solution:
Let y = (sin x
Then log y = log (sin x = x . log (sin x)
Differentiating both sides w.r.t. x, we get
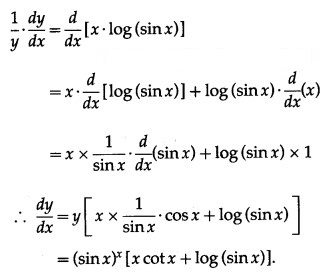
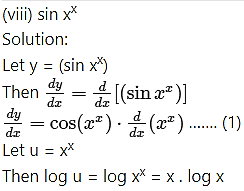
Differentiating both sides w.r.t. x, we get
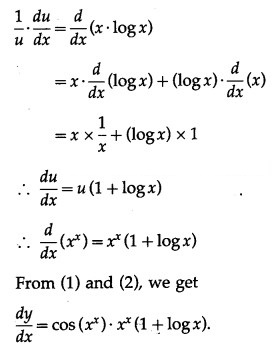
Question 2.
Differentiate the following w.r.t. x:
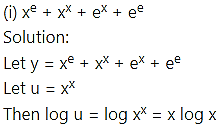
Differentiating both sides w.r.t. x, we get
![]()

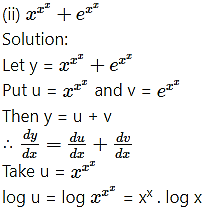
Differentiating both sides w.r.t. x, we get
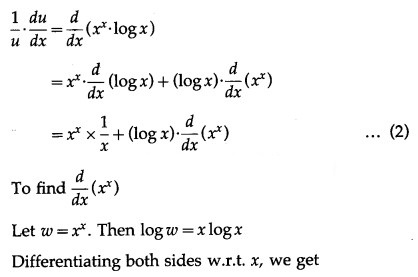
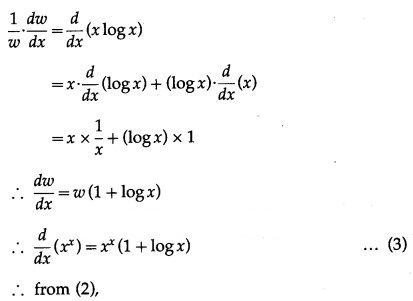

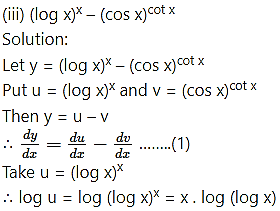
Differentiating both sides w.r.t. x, we get

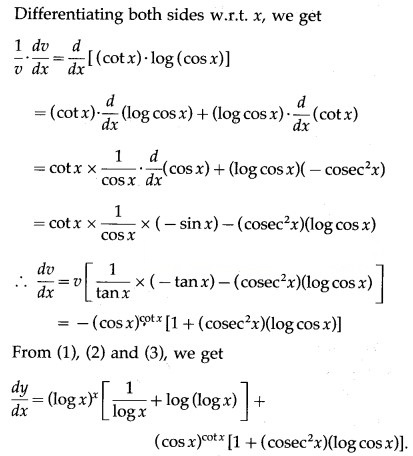
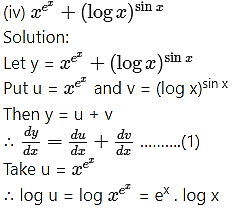
Differentiating both sides w.r.t. x, we get
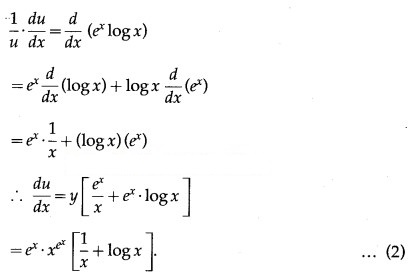
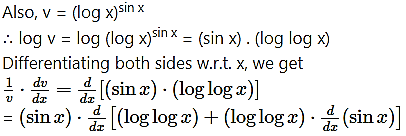
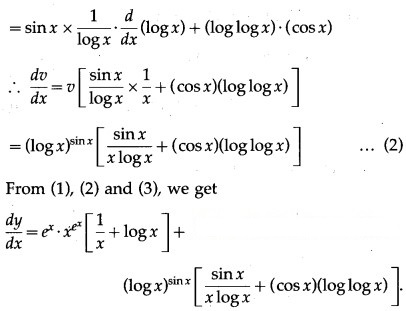
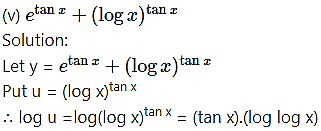
Differentiating both sides w.r.t. x, we get
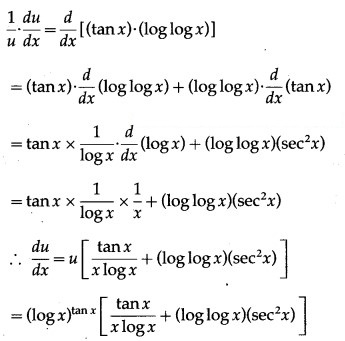
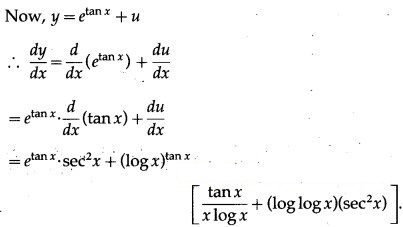
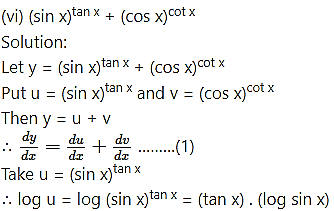
Differentiating both sides w.r.t. x, we get
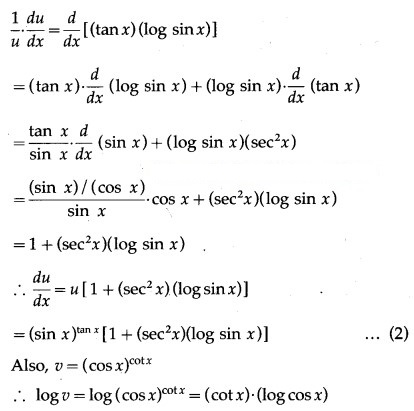
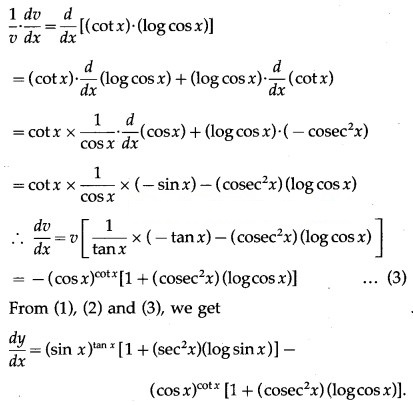




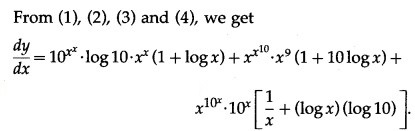

Differentiating both sides w.r.t. x, we get
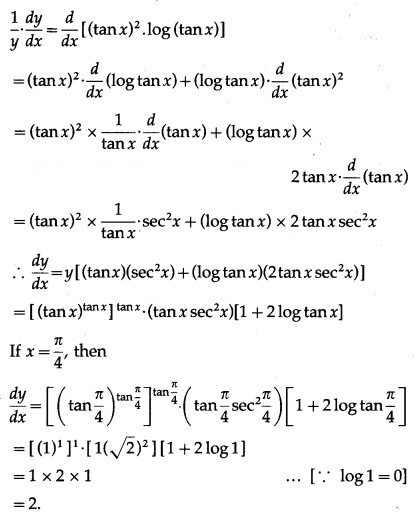
Question 3.![]()
(i) √x + √y = √a
Solution:
√x + √y = √a
Differentiating both sides w.r.t. x, we get
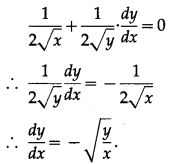
(ii) x√x + y√y = a√a
Solution:
x√x + y√y = a√a
![]()
Differentiating both sides w.r.t. x, we get
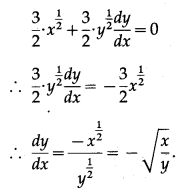
(iii) x + √xy + y = 1
Solution:
x + √xy + y = 1
Differentiating both sides w.r.t. x, we get
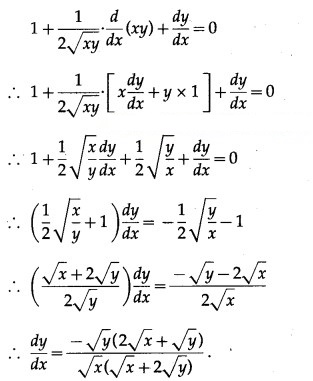
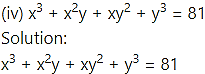
Differentiating both sides w.r.t. x, we get
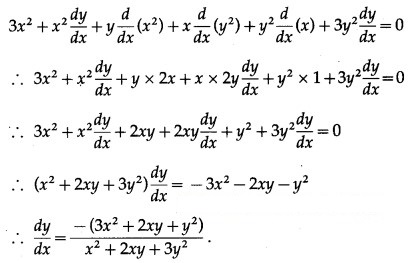
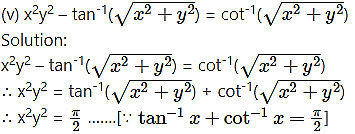
Differentiating both sides w.r.t. x, we get
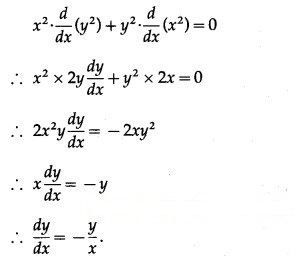
(vi)
Solution:
Differentiating both sides w.r.t. x, we get
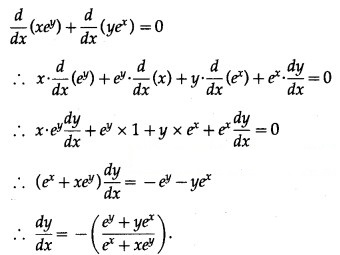
(vii) = cos (x – y)
Solution:
= cos (x – y)
Differentiating both sides w.r.t. x, we get
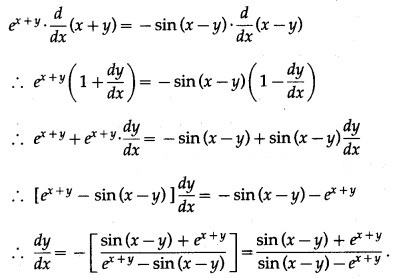
(viii) cos (xy) = x + y
Solution:
cos (xy) = x + y
Differentiating both sides w.r.t. x, we get
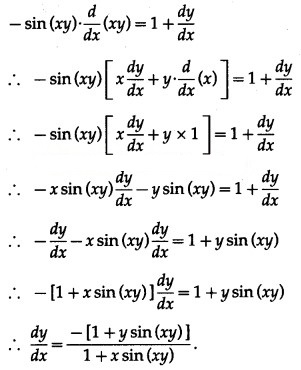
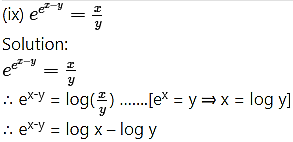
Differentiating both sides w.r.t. x, we get
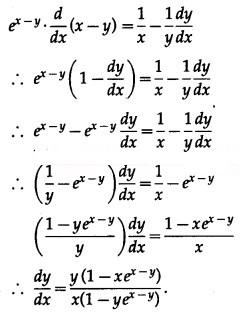
Question 4.
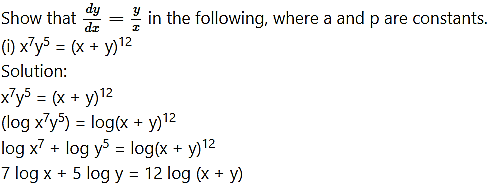
Differentiating both sides w.r.t. x, we get
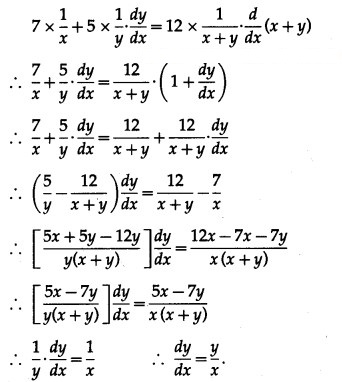
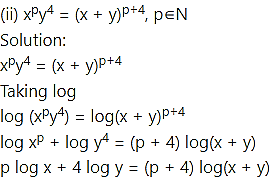
Differentiating both sides w.r.t. x, we get
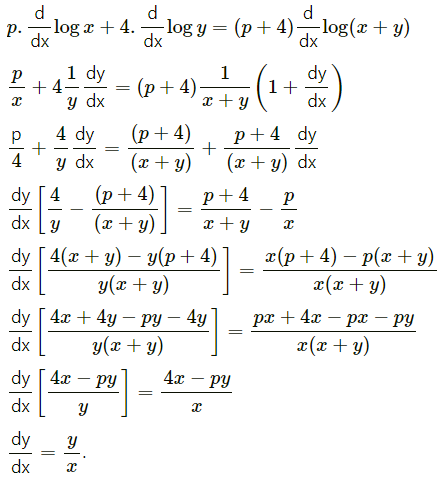
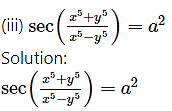
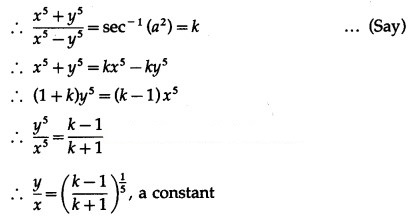
Differentiating both sides w.r.t. x, we get
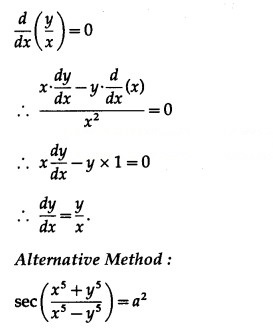
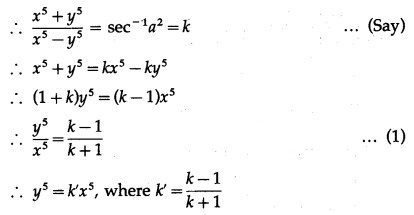
Differentiating both sides w.r.t. x, we get
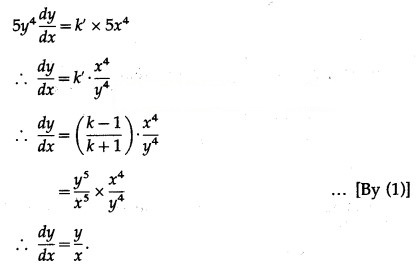
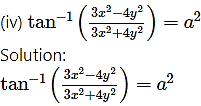
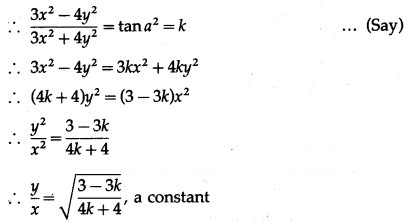
Differentiating both sides w.r.t. x, we get
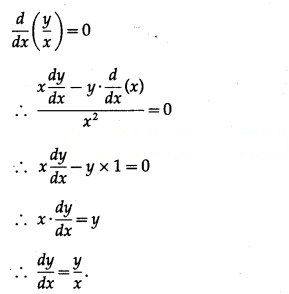
![]()
Solution:
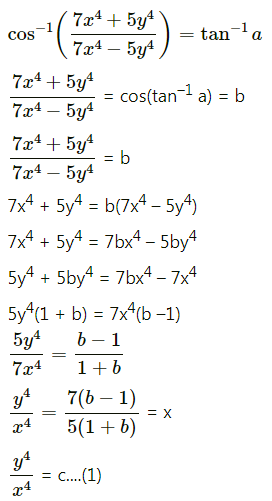
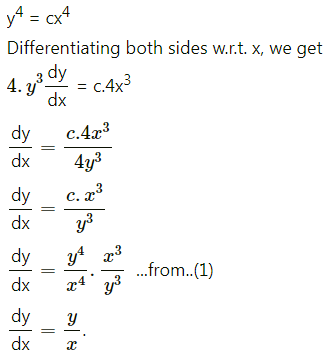
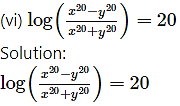
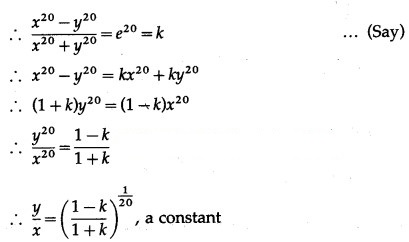
Differentiating both sides w.r.t. x, we get
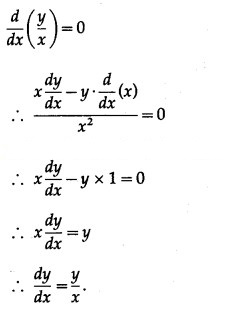
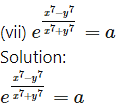
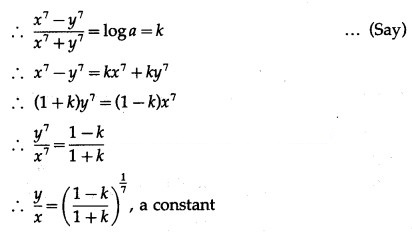
Differentiating both sides w.r.t. x, we get
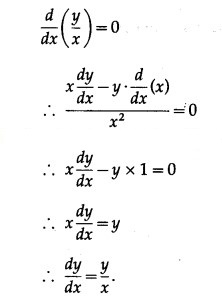
![]()
Solution:
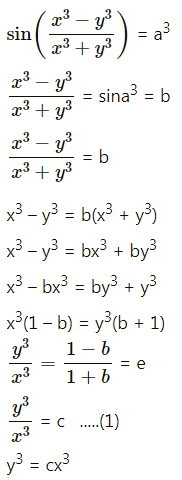
Differentiating both sides w.r.t. x, we get
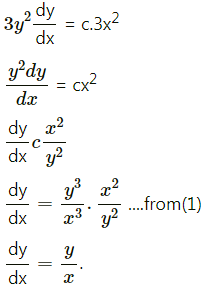
Question 5.
(i) If log (x + y) = log (xy) + p, where p is a constant, then prove that
![]()
Solution:
log (x + y) = log (xy) + p
∴ log (x + y) = log x + log y + p
Differentiating both sides w.r.t. x, we get
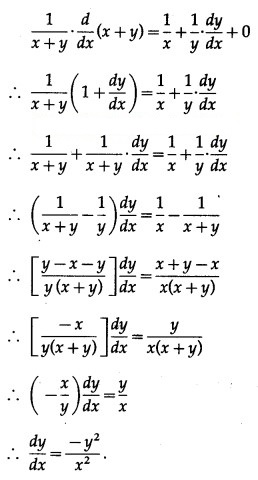


![]()
Solution:
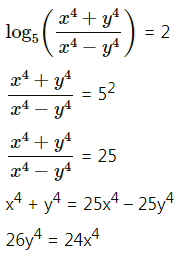
Differentiating both sides w.r.t. x, we get
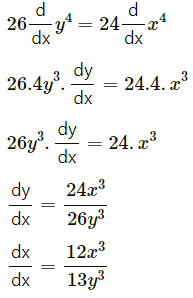

Differentiating both sides w.r.t. x, we get
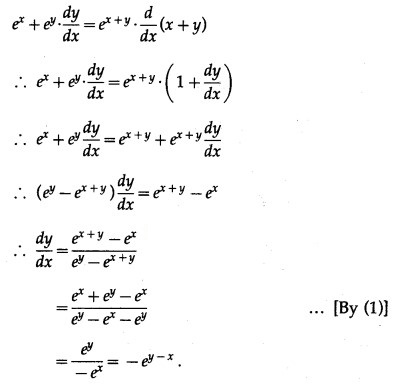
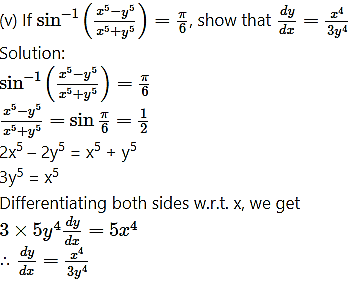
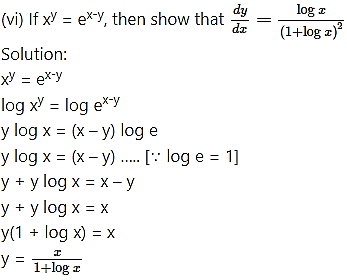

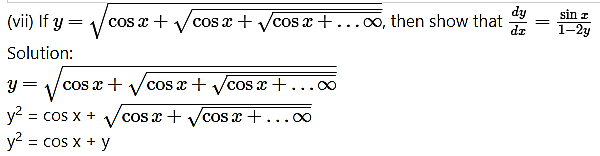
Differentiating both sides w.r.t. x, we get