Chapter 12 Equations in One Variable Set 12.1
Question 1. Each equation is followed by the values of the variable. Decide whether these values are the solutions of that equation.
i. x – 4 = 3, x = – 1, 7, – 7
ii. 9m = 81, m = 3, 9, -3
iii. 2a + 4 = 0, a = 2, – 2, 1
iv. 3 – y = 4, y = – 1, 1, 2
Solution:
i. x – 4 = 3 ….(i)
Substituting x = – 1 in L.H.S. of equation (i),
L.H.S. = (-1) – 4
= – 5
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 1 is not the solution of the given equation.
Substituting x = 7 in L.H.S. of equation (i),
L.H.S. = (7) – 4
= 3
R.H.S. = 3
∴ L.H.S. = R.H.S.
∴ x = 7 is the solution of the given equation.
Substituting x = – 7 in L.H.S. of equation (i),
L.H.S. = (- 7) – 4
= -11
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 7 is not the solution of the given equation.
ii. 9m = 81 …(i)
Substituting m = 3 in L.H.S. of equation (i),
L.H.S. = 9 × (3)
= 27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = 3 is not the solution of the given equation.
Substituting m = 9 in L.H.S. of equation (i),
L.H.S. = 9 × (9)
= 81
R.H.S. = 81
∴L.H.S. = R.H.S.
∴m = 9 is the solution of the given equation.
Substituting m = – 3 in L.H.S. of equation (i),
L.H.S. = 9 × (- 3)
= -27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = – 3 is not the solution of the given equation.
iii. 2a + 4 = 0 …..(i)
Substituting a = 2 in L.H.S. of equation (i),
L.H.S. = 2 (2) + 4
= 4 + 4
= 8
R.H.S. = 0
∴L.H.S. ≠ R.H.S.
∴a = 2 is not the solution of the given equation.
Substituting a = – 2 in L.H.S. of equation (i),
L.H.S. = 2 (-2)+ 4
= -4 + 4
= 0
R.H.S. = 0
∴L.H.S. = R.H.S.
∴a = – 2 is the solution of the given equation.
Substituting a = 1 in L.H.S. of equation (i),
L.H.S. = 2(1)+ 4
= 2 + 4
= 6
R.H.S. = 0
∴ L.H.S. ≠ R.H.S.
∴a = 1 is not the solution of the given equation.
iv. 3 – y = 4 …(i)
Substituting y = -1 in L.H.S. of equation (i),
L.H.S. = 3 – (- 1)
= 3 + 1
= 4
R.H.S. = 4
∴L.H.S. = R.H.S.
∴y = – 1 is the solution of the given equation.
Substituting y = 1 in L.H.S. of equation (i),
L.H.S. = 3-(1)
= 2
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 1 is not the solution of the given equation.
Substituting y = 2 in L.H.S. of equation (i),
L.H.S. = 3-(2)
= 1
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 2 is not the solution of the given equation.
Question 2.
Solve the following equations:
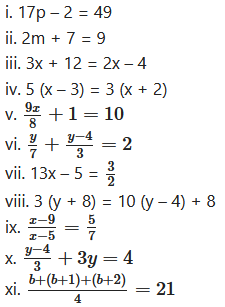
Solution:
i. 17p – 2 = 49
∴ 17p – 2 + 2 = 49 + 2
…[Adding 2 on both the sides]
∴ 17p = 51
![]()
p = 3
ii. 2m + 7 = 9
∴ 2m + 7 – 7 = 9 – 7
…[Subtracting 7 from both the sides]
∴ 2m = 2
![]()
∴ m = 1
iii. 3x + 12 = 2x – 4
∴ 3x + 12 – 12 = 2x – 4 – 12
…[Subtracting 12 from both the sides]
∴ 3x = 2x – 16
∴ 3x – 2x = 2x – 16 – 2x
…[Subtracting 2x from both the sides]
∴ x = – 16
iv. 5 (x – 3) = 3 (x + 2)
∴ 5x – 15 = 3x + 6
∴ 5x – 15 + 15 = 3x + 6 + 15
…[Adding 15 on both the sides]
∴ 5x = 3x + 21
∴ 5x – 3x = 3x + 21 – 3x
…[Subtracting 3x from both the sides]
∴ 2x = 21


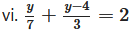


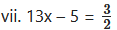

viii. 3 (y + 8) = 10 (y – 4) + 8
∴ 3y + 24 = 10y – 40 + 8
∴ 3y + 24 = 10y – 32
∴ 3y + 24 – 24 = 10y – 32 – 24
…[Subtracting 24 from both the sides]
∴ 3y = 10y – 56
∴ 3y – 10y = 10y – 56
…[Subtracting 10y from both the sides]
∴ – 7y = – 56
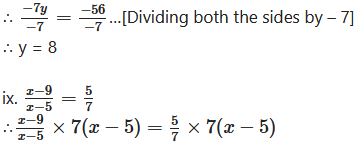
…[Multiplying both the sides by 7 (x – 5)]
∴7 (x – 9) = 5 (x – 5)
∴7x – 63 = 5x – 25
∴7x – 63 + 63 = 5x – 25 + 63
…[Adding 63 on both the sides]
∴7x = 5x + 38
∴7x – 5x = 5x + 38 – 5x
…[Subtracting 5x from both the sides]
∴ 2x = 38

…[Multiplying both the sides by 4]
∴b + b + 1 + b + 2 = 84
∴3b + 3 = 84
∴3b + 3 – 3 = 84 – 3
…[ Subtracting 3 from both the sides]
∴3b = 81
∴\(\frac{3 b}{3}=\frac{81}{3}[/latex …[Dividing both the sides by 3]
∴b = 27
Intext Questions and Activities
Question 1.
Fill in the boxes to solve the following equations. (Textbook pg. no. 75)
i. x + 4 = 9
∴x + 4 – __ = 9 – __
… [Subtracting 4 from both the sides]
∴ x = __
ii. x – 2 = 7
∴x – 2 + __ = 7 + __
… [Adding 2 on both the sides]
∴x = __
iii. [latex]\frac { x }{ 3 }=4\)
∴ × __ = 4 ×__
∴x = __
iv. 4x = 24
∴ __ = __
∴x = __
Solution:
i. x + 4 = 9
∴x + 4 – 4 = 9 – 4
… [Subtracting 4 from both the sides]
∴ x = 5
ii. x – 2 = 7
∴x – 2 + 2 = 7 + 2
… [Adding 2 on both the sides]
∴x = 9
iii. x/3=4
∴x/3× 3 = 4 × 3
… [Multiplying both the sides by 3]
∴x = 12
iv. 4x = 24
![]()
… [Dividing both the sides by 4]
∴x = 6