Chapter 15 Area 15.2

Question 3.
If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?
Solution:
Let ₹ABCD be the rhombus. Diagonals AC and BD intersect at point E.
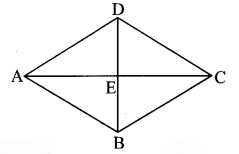

In ∆ADE,
m ∠AED = 90° …[Diagonals of a rhombus are perpendicular to each other]
∴ [l(AD)]² = [l(AE)]² + [l(DE)]² … [Pythagoras theorem]
∴ (25)² = (24)² + l(DE)² … [From (ii) and (iii)]
∴ 625 = 576 + l(DE)²
∴ l(DE)² = 625 – 576
∴ l(DE)² = 49
∴ l(DE) = √49
… [Taking square root of both sides]

Question 4.
If length of a diagonal of a rhombus is 30 cm and its area is 240 sq.cm, find its perimeter.
Solution:
Let ₹ABCD be the rhombus.
Diagonals AC and BD intersect at point E.
l(AC) = 30 cm …(i)
and A(₹ABCD) = 240 sq. cm .. .(ii)
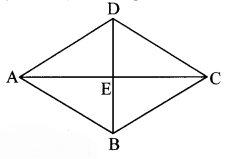

In ∆ADE,
m∠AED = 90°
…[Diagonals of a rhombus are perpendicular to each other]
∴[l(AD)]² = [l(AE)]² + [l(DE)]²
…[Pythagoras theorem]
∴l(AD)² = (15)² + (8)² … [From (iv) and (v)]
= 225 + 64
∴l(AD)² = 289
∴l(AD) = √289
…[Taking square root of both sides]
∴l(AD) = 17 cm
Perimeter of rhombus = 4 × side
= 4 × l(AD)
= 4 × 17
= 68 cm
∴The perimeter of the rhombus is 68 cm.