MARCH 2019 – Maharashtra Board Solutions

MARCH 2019

MATHEMATICS PART-II

General Instructions :

(1) All questions are compulsory.

(2) Use of calculator is not allowed.

(3) Figures to the right of qusetions indicate full marks.

(4) Draw proper figures for answers wherever necessary.

(5) The marks for construction should be clear and distinct. Do not erase them.

(6) While writing any proof, drawing relevant figure is necessary. Also the proof should be consistent with the figure.

Q 1. (A) Solve the following questions (Any four):

(i) If and , then ?

Solution

(i) Given,

(ii) In right-angled , if , then find .

Solution

Given, In .

Using Pythagoras theorem,

(iii) Write the length of largest chord of a circle with radius .

Solution

Given, radius .

Largest chord of a circle is the diameter of that circle.

Length of largest chord diameter

(iv) From the given number line, find :

Solution

Given,

(v) Find the value of .

Solution

(vi) Find the area of a circle of radius .

Solution

Given, .

(B) Solve the following questions (Any two):

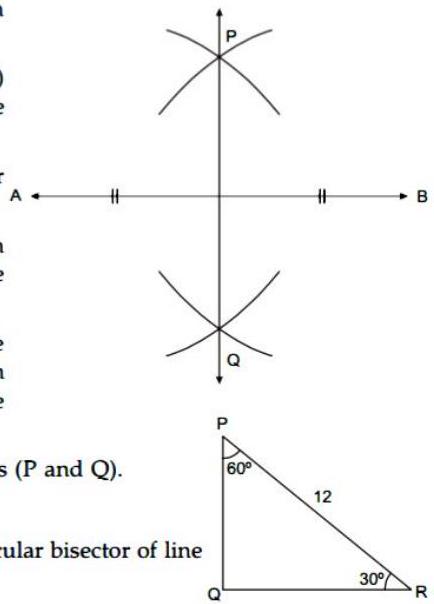
(i) Draw seg of length and bisect it.

Solution

Steps of construction :

(1) Draw a line segment of length .

(2) Keep the compass at one end (A) of the line segment (It can be either of the ends).

(3) Adjust the compass length to over more than half the line segment.

(4) With this length, draw arcs on each side of the line segment (at the top and at the bottom).

(5) Without changing the width of the compass, keep the compass on point and draw arcs on each side of the segment .

(6) Now, we get two arc intersections (P and Q).

(7) Draw line .

(8) Line is the required perpendicular bisector of line segment .

(ii) In right-angled triangle , if and , then find the values of and .

Solution

Given, In .

(iii) In a right circular cone, if perpendicular height is and radius is , then find its slant height.*

Solution

Answer is not given due to the reduced syllabus.

Q 2. (A) Choose the correct alternative :

(i) and are equilateral triangles. If and , then what is the length of ?
(a)
(b) 4
(c) 8
(d)

Solution

(d)

(ii) Out of the following which is a Pythagorean triplet?
(a)
(b)
(c)
(d)

Solution

(c)

(iii) is inscribed in arc of a circle with centre . If , find (arc ACB) :
(a)
(b)
(c)
(d)

Solution

(iv) ?
(a)
(b)
(c)
(d)

Solution

(b)

(B) Solve the following questions (Any two) :

(i) Construct tangent to a circle with centre and radius at any point on it.

Solution

Steps of construction :

(1) Draw a circle with centre $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{AE341717-B63C-464A-89A4-C1A7CBA51D10}$ and radius AP, $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{679EDF61-51B0-491F-BF8F-4235608F37EA}$ AP) $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{884A7CF0-D595-4104-9D39-D0AD16A80384}$ $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{C0A91E51-4258-4F84-8F8F-878A027E2A08}$ .

(2) Draw a ray $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{26DE35F8-4AF4-4545-BD87-81CBA4F0CF00}$ .

(3) Take a point $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{E9171E77-B8B9-406B-BFD5-3BFC5B1837F2}$ on ray $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{9D89BF84-BF32-48DB-B063-5A405302A8CB}$ such that $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{BEF88BF6-D021-473A-8312-28F028EC82FB}$

(4) Draw a perpendicular bisector of $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{0D1AF496-4B98-481F-80CA-6786923D872E}$ (Name it as $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{BA18963F-8C00-4FE1-B0B9-A2E1260D2F73}$ ).

(5) Line $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{BA18963F-8C00-4FE1-B0B9-A2E1260D2F73}$ is a required tangent to the circle at point $C:\Users\Raaz\AppData\Local\Microsoft\Windows\Clipboard\HistoryData\{B93E1304-531C-46BC-A811-51DA2678BE85}\{657B3D45-1483-4628-9002-B08458B166AC}\ResourceMap\{3A3E7C5B-C7BC-4972-9E52-FA9600982852}$ on it.

(ii) Find slope of a line passing through the points and .”

Solution

Answer is not given due to the reduced syllabus.

(iii) Find the surface area of sphere of radius .

Solution

Answer is not given due to the reduced syllabus.

Q 3. (A) Complete the following activities (Any two) :

Solution

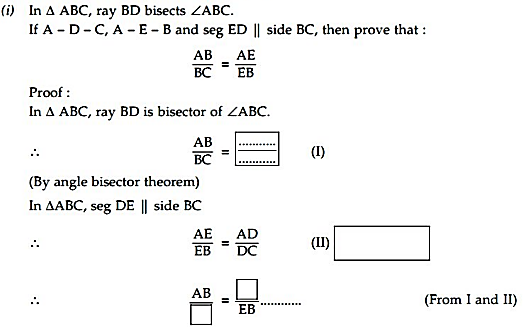
In , ray bisects .

If and seg side , then prove that :

Proof :

In , ray is bisector of .

In , seg side

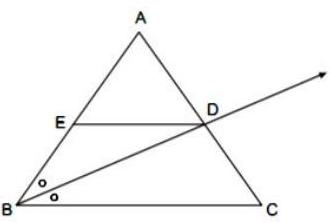
(ii) Prove that, angles inscribed in the same arc are congruent.

Given : and are inscribed in the same arc.

Arc PXR is intercepted by the angles.

(Angles equal in measure are congruent)

Solution

Prove that, angles inscribed in the same arc are congruent.

Given : and are inscribed in the same arc.

Arc PXR is intercepted by the angles.

To prove :

Proof :

..(I) Inscribed angle theorem

(Angles equal in measure are congruent)

(iii) How many solid cylinders of radius and height can be made by melting a solid sphere of radius ?”

Activity : Radius of the sphere,

For cylinder, radius , height

Number of cylinders can be made

Volume of the sphere

Solution

Answer is not given due to the reduced syllabus..

(B) Solve the following questions (Any two):

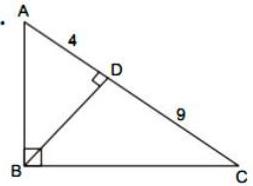
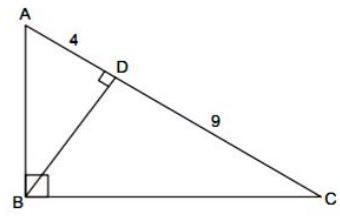
(i) In right-angled . If , then find .

Solution

Given, In right-angled and .

In ,

(ii) Verify whether the following points are collinear or not :

Solution

Answer is not given due to the reduced syllabus.

(iii) If , then find the value of .

Solution

Given,

Q 4. Solve the following questions (Any three) :

(i) In , seg is a median, and .

Find the length of .

Solution

Given, In , seg is a median.

Also, .

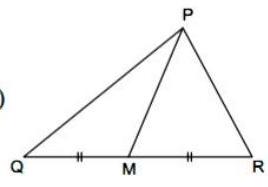
is a median of the .

is the mid point of .

(ii) In the given figure, is centre of circle, and PYR , then find the value of each of the following :

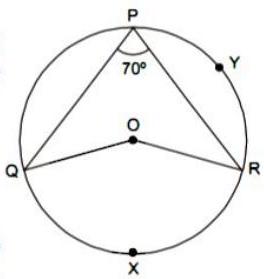
(a) (arc QXR)

Solution

Given : In fig., is the centre of circle.

is inscribed in the arc QXR.

(b)

Solution

Measure of the central angle is equal to the corresponding minor arc.

(c)

Solution

is inscribed in the arc

(iii) Draw a circle with radius . Construct tangents to the circle from a point at a distance of from the centre.

Solution

Steps of construction :

(1) Draw a circle with centre and radius .

(2) Draw ray OX.

(3) Take a point on ray such that .

(4) Draw a perpendicular bisector of which intersect ray at point M.

(5) Taking as a centre and as radius, draw a circle, which cuts the circle with centre at point and B.

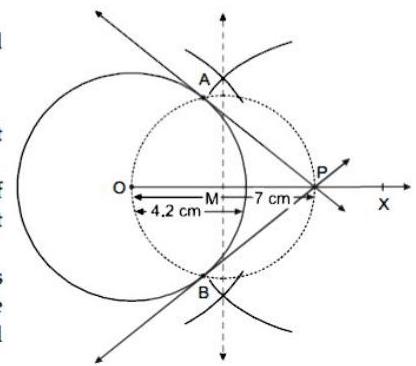
(6) Draw ray PA and ray PB.

Line and line are the required tangents to the circle from point at a distance of from the centre.

Q 5. Solve the following questions

(i) A circle with centre is inscribed in the . Side , side and side touch the circle at points ,

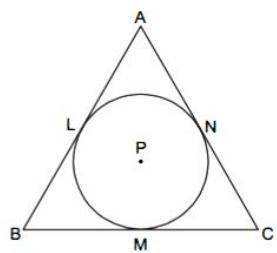
and respectively. Radius of the circle is .

Prove that :

Solution

Given, In the figure, the circle with centre is inscribed in the . Side , side , side touch the circle at points and respectively. Radius of the circle is .

To prove that :

Construction : We draw the radii PM, , and .

Also, we draw seg PA, seg PB, seg PC.

Proof : In a circle with centre P, seg PL, seg PM and seg

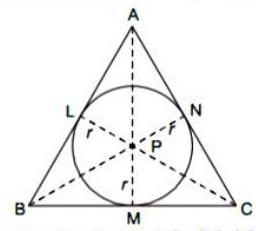
are the radii and seg. , seg , seg are the tangents at point respectively.

seg side

seg side (By the theorem, tangent is perpendicular to the radius)

We know,

Similarly,

Adding equations (i), (ii) and (iii), we get

Hence Proved.

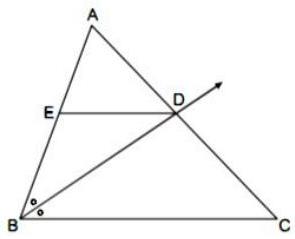
(ii) In . seg side and seg is angle bisector of .

Prove that :

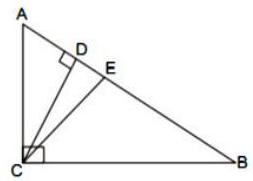
Solution

Given, In ,

seg CE is angle bisector .

To prove that :

Proof : In

seg CE is angle bisector of .

Squaring both the sides

Dividing both the sides by

Now, in figure

(Right angled triangle similarity property)

Consider,

Q 6. Solve the following questions (Any one) :

(i) Show that the points and are the vertices of a triangle. Also state with the reason the type of the triangle.

Solution

Let, .

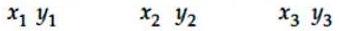
By distance formula,

From equations (i), (ii) and (iii),

The three points are the vertices of triangle as sum of length of any two sides is greater than the third side of the triangle. Hence Proved. This triangle is an isosceles triangle as the two sides are equal.

(ii) In the above figure, XLMT is a rectangle. . Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.

Solution

Answer is not given due to the reduced syllabus.

(iv) When an observer at a distance of from a tree looks at the top of the tree, the angle of elevation is . What is the height of the tree?

Solution

Answer is not given due to the reduced syllabus.