Blog

Chapter 7 Mensuration Set 7.3

Chapter 7 Mensuration Set 7.3

Question 1.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given : Radius (r) = 10 cm,
Measure of the arc (θ) = 54°
To find : Area of the sector.

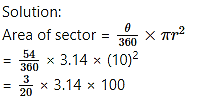
= 3 × 3.14 × 5
= 15 × 3.14
= 47.1 cm²
∴ The area of the sector is 47.1 cm².

Question 2.
Measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14)
Given: Radius (r) = 18 cm,
Measure of the arc (θ) = 80°
To find: Length of the arc.

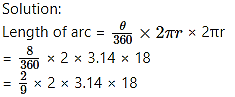
= 2 × 2 × 3.14 × 2 = 25.12 cm
∴ The length of the arc is 25.12 cm.

Question 3.
Radius of a sector of a circle is 3.5 cm and length of its arc is 2.2 cm. Find the area of the sector.
Solution:
Given: Radius (r) = 3.5 cm,
length of arc (l) = 2.2 cm
To find: Area of the sector.
Solution:

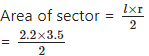
= 1.1 × 3.5 = 3.85 cm²
∴ The area of the sector is 3.85 cm².

Question 4.
Radius of a circle is 10 cm. Area of a sector of the circle is 100 cm². Find the area of its corresponding major sector, (π = 3.14)
Given: Radius (r) = 10 cm,
area of minor sector =100 cm²
To find: Area of maj or sector.
Solution:
Area of circle = πr²
= 3.14 × (10)²
= 3.14 × 100 = 314 cm²
Now, area of major sector
= area of circle – area of minor sector
= 314 – 100
= 214 cm²
∴ The area of the corresponding major sector is 214 cm².

Question 5.
Area of a sector of a circle of radius 15 cm is 30 cm². Find the length of the arc of the sector.
Given: Radius (r) =15 cm,
area of sector = 30 cm²
To find: Length of the arc (l).
Solution:

∴ The length of the arc is 4 cm.

Question 6.
In the adjoining figure, radius of the circle is 7 cm and m (arc MBN) = 60°, find
i. Area of the circle.
ii. A(O-MBN).
iii. A(O-MCN).

Given: radius (r) = 7 cm,
m(arc MBN) = θ = 60°
Solution:
i. Area of circle = πr²
= 22/7 × (7)²
= 22 × 7
= 154 cm²
∴ The area of the circle is 154 cm²

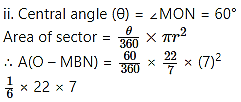
= 25.67 cm²
= 25.7 cm²
∴ A(O-MBN) = 25.7 cm²

iii. Area of major sector = area of circle – area of minor sector
∴ A(O-MCN) = Area of circle – A(O-MBN)
= 154 – 25.7
∴ A(O-MCN) = 128.3 cm²

Question 7.
In the adjoining figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm. Find A(P-ABC).
Given: Radius (r) = 3.4 cm,
perimeter of sector 12.8 cm
To find: A(P-ABC)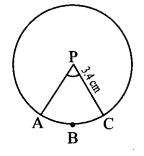

Solution:
Perimeter of sector
= Iength of arc ABC + AP + CP

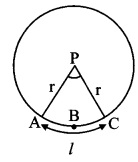
∴ 12.8 = l + 3.4 + 3.4
∴ 12.8 = l + 6.8
∴ l = 12.8 – 6.8 = 6cm

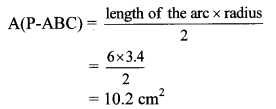
∴ A(P-ABC) = 10.2 cm²

Question 8.
In the adjoining figure, O is the centre of the sector. ∠ROQ = ∠MON = 60°. OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and (π = 22/7)

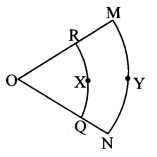
Given: ∠ROQ = ∠MON = 60°,
radius (r) = OR = 7 cm, radius (R) = OM = 21 cm
To find: Lengths of arc RXQ and arc MYN.

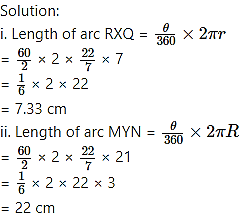
∴ The lengths of arc RXQ and arc MYN are 7.33 cm and 22 cm respectively.

Question 9.
In the adjoining figure, if A(P-ABC) = 154 cm², radius of the circle is 14 cm, find
i. ∠APC,
ii. l(arc ABC).

Given: A(P – ABC) = 154 cm²,
radius (r) = 14 cm
Solution:
i. Let ∠APC = θ

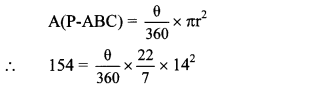
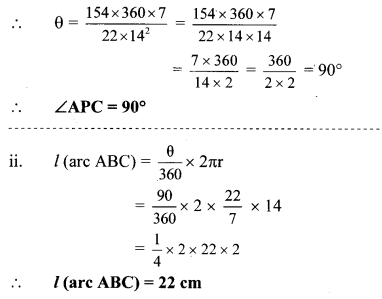
Question 10.
Radius of a sector of a circle is 7 cm. If measure of arc of the sector is
i. 30°
ii. 210°
iii. three right angles, find the area of the sector in each case.
Given: Radius (r) = 7 cm
To find: Area of the sector.
Solution:
i. Measure of the arc (θ) = 30°

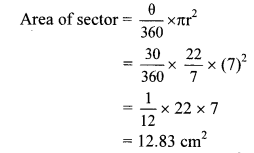
∴ Area of the sector is 12.83 cm².
ii. Measure of the arc (θ) = 210°

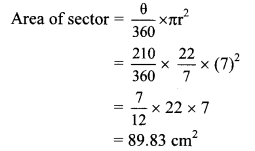
∴ Area of the sector is 89.83 cm².
iii. Measure of the arc (θ) = 3 right angle
= 3 × 90° = 270°

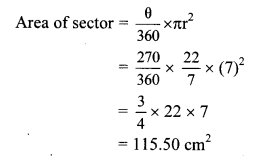
∴ Area of the sector is 115.50 cm².

Question 11.
The area of a minor sector of a circle is 3.85 cm² and the measure of its central angle is 36°. Find the radius of the circle.
Given: Area of minor sector = 3.85 cm²,
central angle (θ) = 36°
To find: Radius of the circle (r).
Solution:
Area of minor sector = θ360×πr2

∴ The radius of the circle ¡s 3.5 cm.

Question 12.
In the given figure, ꠸PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y and z.

Given: In rectangle PQRS,
PQ = 14 cm, QR = 21 cm
To find: Areas of the parts x, y and z.
Solution:

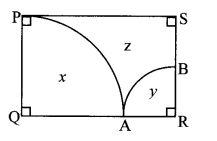
∠Q = ∠R = θ = 90° …[Angles of a rectangle]

For the sector (Q – PA),
PQ = QA …[Radii of the same circle]
∴ QA = 14 cm
Now, QR = QA + AR … [Q – A – R]
∴ 21 = 14 + AR
∴ AR = 7 cm

Area of rectangle = length × breadth
area of ꠸PQRS = PQ × QR
= 14 × 21
= 294 cm²
Area of part z = area of ꠸PQRS
– area of part x – area of part y
= 294 – 154 – 38.5
= 101.5 cm²
∴ The area of part x is 154 cm², the area of part y is 38,5 cm² and the area of part z is 101.5 cm².

Question 13.
∆ALMN is an equilat triangle. LM = 14 cm. As shown in figure, three sectors are drawn with vertices as centres and radius 7 cm. Find,

i. A (∆ LMN).
ii. Area of any one of the sectors.
iii. Total area of all the three sectors.
iv. Area of the shaded region. (√3 = 1.732 )
Given: In equilateral triangle LMN, LM =14 cm,
radius of sectors (r) = 7 cm
Solution:
i. ∆LMN is an equilateral triangle.

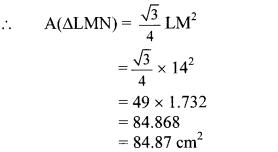
ii. Central angle (θ) = 60° …[Angle of an equilateral triangle]

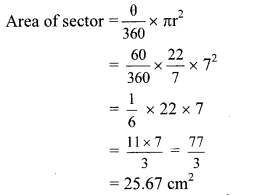
∴ Area of one sector = 25.67 cm²
iii. Total area of all three sectors
= 3 × Area of one sector
= 3 × 25.67
= 77.01 cm²
∴ Total area of all three sectors = 77.01 cm²
iv. Area of shaded region
= A(∆LMN) – total area of all three sectors
= 84.87 – 77.01
= 7.86 cm²
∴ Area of shaded region = 7.86 cm

Intext Questions and Activities

Question 1.
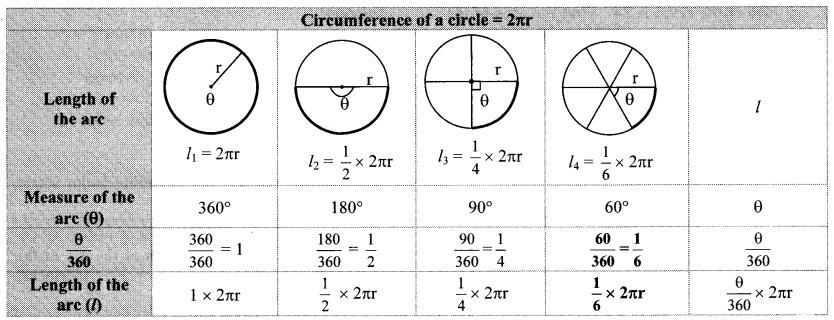
Complete the following table with the help of given figure. (Textbook pg. no. 149)


Solution:

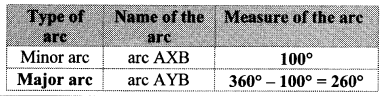
Question 2.
Observe the figures below. Radii of all circles are equal. Observe the areas of the shaded regions and complete the following table. (Textbook pg. no. 150)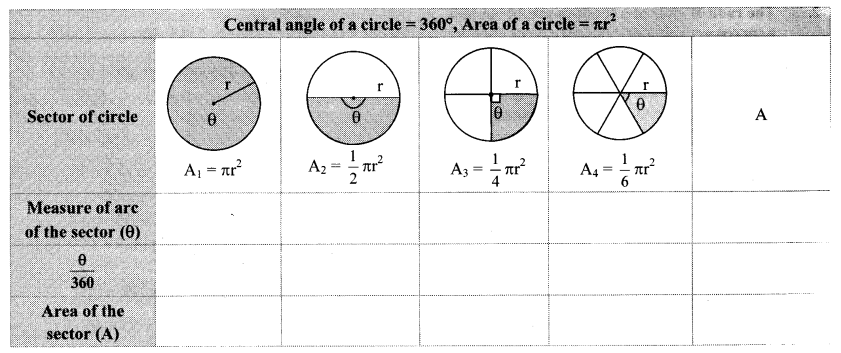

Solution:

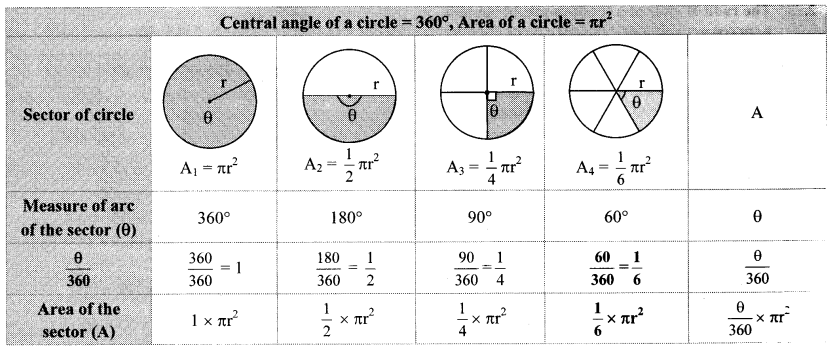
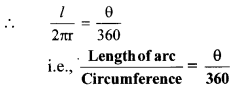
Thus, if measure of an arc of a circle is θ, then

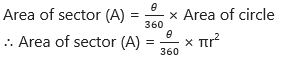
Question 3.
In the following figures, radii of all circles are equal. Observe the length of arc in each figure and complete the table. (Textbook pg. no. 151)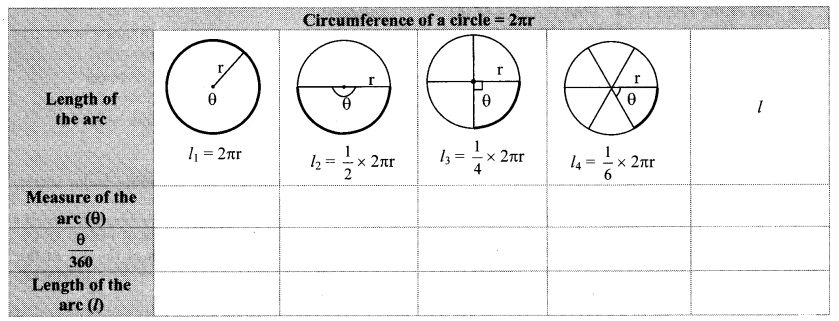

Solution: