Chapter 1 Angle and its Measurement Ex 1.1
Chapter 1 Angle and its Measurement Ex 1.1
Question 1.
(A) Determine which of the following pairs of angles are co-terminal.
i. 210°, 150°
ii. 360°, -30°
iii. -180°, 540°
iv. -405°, 675°
v. 860°, 580°
vi. 900°, -900°
Solution:
210°,- 150°
210°-(- 150°) = 210°+ 150°
= 360°
= 1 (360°),
which is a multiple of 360°.
∴ The given pair of angles is co-terminal.
ii. 360°, – 30°
360° – (- 30°) = 360° + 30°
= 390°,
which is not a multiple of 360°.
∴ The given pair of angles is not co-terminal.
iii. -180°, 540°
540° -(-180°) = 540°+ 180°
= 720°
= 2(360°),
which is a multiple of 360°.
.’. The given pair of angles is co-terminal.
iv. – 405°, 675°
675° – (- 405°) = 675° + 405°
= 1080°
= 3(360°),
which is a multiple of 360°.
.’. The given pair of angles is co-terminal.
v. 860°, 580°
860° – 580° = 280°
which is not a multiple of 360, °.
∴ The given pair of angles is not co-terminal.
vi. 900°, 900°
900° – (-900°) = 900° + 900°
= 1800°
= 5(360°)
which is a multiple of 360°
∴ The given pair of angles is co-terminal.
Question 1.
(B) Draw the angles of the following measures and determine their quadrants.
i. -140°
ii. 250°
iii. 420°
iv. 750°
v. 945°
vi. 1120°
vii. – 80°
viii. – 330°
ix. – 500°
x. – 820°
Solution:

From the figure, the given angle terminates in quadrant III.
ii.
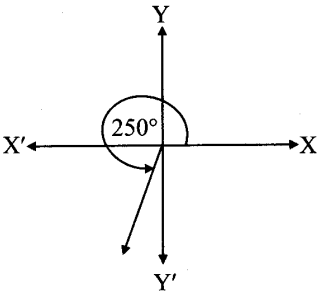
From the figure, the given angle terminates in quadrant III.
iii.
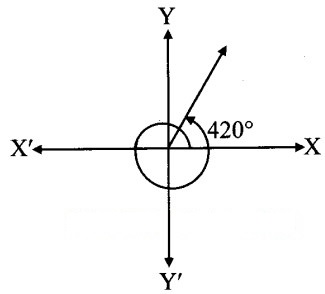
From the figure, the given angle terminates in quadrant I.
iv.
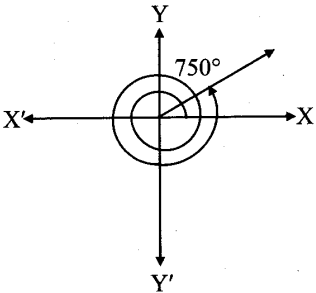
From the figure, the given angle terminates in quadrant I.
v.
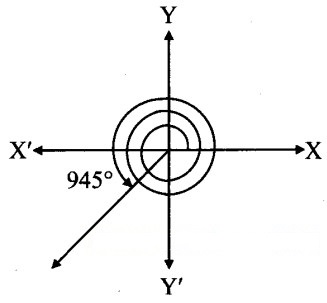
From the figure, the given angle terminates in quadrant III.
vi.
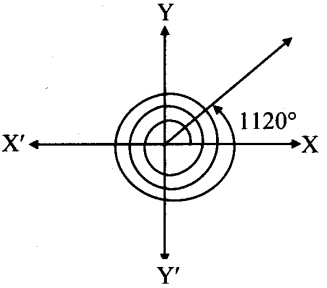
From the figure, the given angle terminates in quadrant I.
vii.
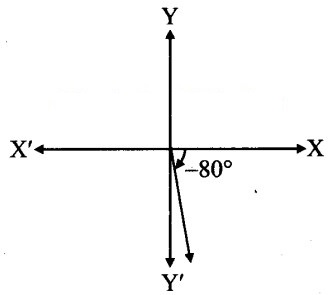
From the figure, the given angle terminates in quadrant IV.
viii.
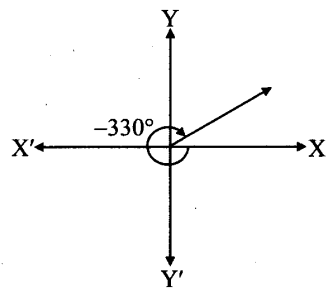
From the figure, the given angle terminates in quadrant I.
ix.
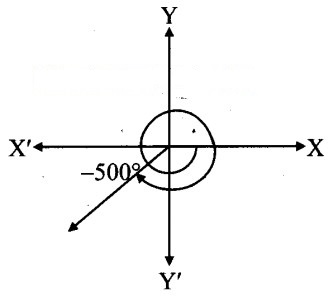
From the figure, the given angle terminates in quadrant III.
[Note: Answer given in the textbook is ‘Angle lies in quadrant II’. However, we found that it lies in quadrant III.]
x.
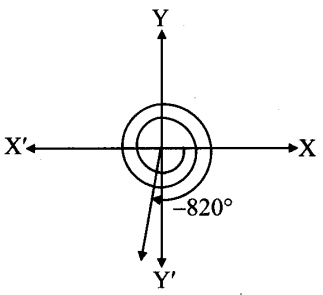
From the figure, the given angle terminates in quadrant III.
Question 2.
Convert the following angles into radians,
i. 85°
ii. 250°
iii. -132°
iv. 65°30′
v. 75°30′
vi. 40°48′
Solution:

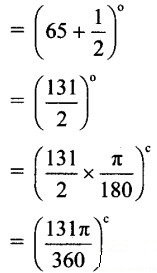
v. 75° 30′ = 75° + 30′

vi. 40°48′ = 40° + 48′
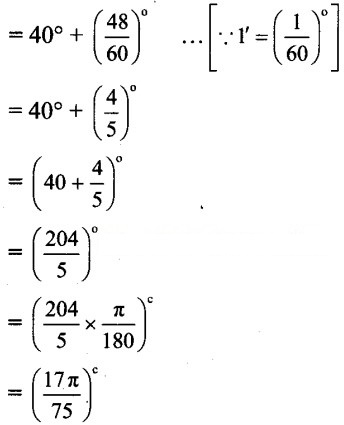
Question 3.
Convert the following angles in degrees.
Solution:
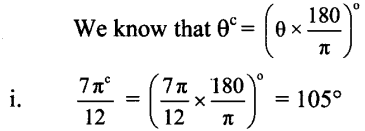
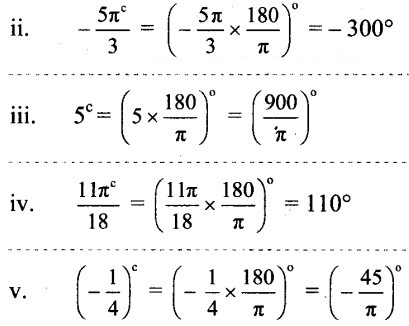
Question 4.
Express the following angles in degrees, minutes and seconds.
i. (183.7)°
ii. (245.33)°![]()
Solution:
We know that 1° = 60′ and 1′ = 60″
i. (183.7)° = 183° +(0.7)°
= 183° + (0.7 x 60)’
= 183°+ 42′
= 183° 42′
ii. (245.33)° = 245° + (0.33)°
= 245° + (0.33 x 60)’
= 245° + (19.8)’
= 245° + 19’+ (0.8)’
= 245° 19’+ (0.8 x 60)”
= 245° 19’+ 48″
= 245° 19′ 48″
![]()
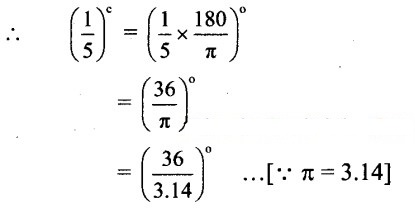
= (11.46)°
= 11° +(0.46)°
= 11° + (0.46×60)’
= 11°+ (27.6)’
= 11°+ 27’+ (0.6)’
= 11° + 27′ + (0.6×60)”
= 11°27′ + 36″
= 11°27’36” (approx.)
Question 5.
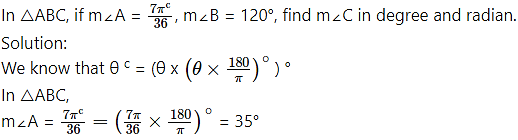
m∠B = 120°
∴ m∠A + m∠B + m∠C = 180°
… [Sum of the angles of a triangle is 180°]
∴ 35° + 120° + m∠C = 180° m∠C = 180° – 35° – 120°
∴ m∠C = 25°
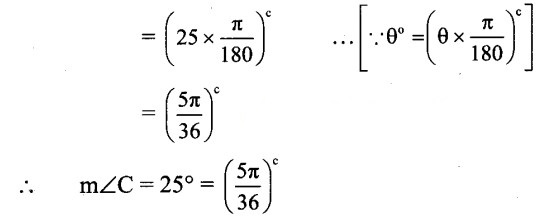
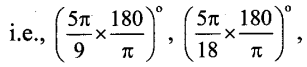
Question 6.

i.e., 100°, 50°
Let the measure of third angle of the triangle be x°.
∴ 100°+50°+x° = 180°
…[Sum of the angles of a triangle is 180°]
∴ x° = 180°- 100° – 50°
∴ x° = 30°


Question 7.
In a right angled triangle, the acute angles are in the ratio 4:5. Find the angles of the triangle in degrees and radians.
Solution:
Since the triangle is aright angled triangle, one of the angles is 90°.
In the right angled triangle, the acute angles are in the ratio 4:5.
Let the measures of the acute angles of the triangle in degrees be 4k and 5k, where k is a constant.
∴ 4k + 5k+ 90°= 180°
… [Sum of the angles of a triangle is 180°]
∴ 9k = 180° – 90°
∴ 9k = 90°
∴ k = 10°
∴ The measures of the angles in degrees are
4k = 4 x 10° = 40°,
5k = 5 x 10° = 50°
and 90°.
![]()
∴ The measure of the angles in radius are
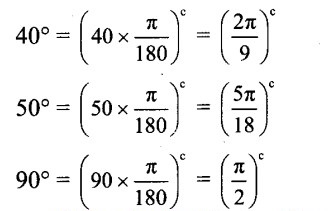
Question 8.
The sum of two angles is 5πc and their difference is 60°. Find their measures in degrees.
Solution:
Let the measures of the two angles in degrees be x and y.
Sum of two angles is 5πc
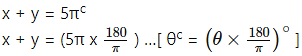
∴ x + y = 900° ………..(i)
∴ Difference of two angles is 60°.
x – y = 60° ….(ii)
Adding (i) and (ii), we get
2x = 960°
∴ x = 480°
Substituting the value of x in (i), we get
480° + y = 900°
∴ y = 900° — 480° = 420°
∴ The measures of the two angles in degrees are 480° and 420°.
Question 9.
The measures of the angles of a triangle are in the ratio 3:7:8. Find their measures in degrees and radians.
Solution:
The measures of the angles of the triangle are in the ratio 3:7:8.
Let the measures of the angles of the triangle in degrees be 3k, 7k and 8k, where k is a constant.
∴ 3k + 7k + 8k = 180°
… [Sum of the angles of a triangle is 180°]
∴ 18k =180°
∴ k = 10°
∴ The measures of the angles in degrees are
3k = 3 x 10° = 30°,
7k = 7 x 10° = 70° and
8k = 8 x 10° = 80°.
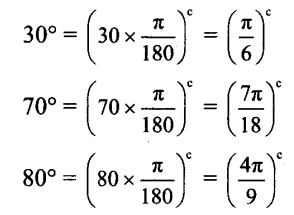
Question 10.
The measures of the angles of a triangle are in A.P. and the greatest is 5 times the smallest (least). Find the angles in degrees and radians.
Solution:
Let the measures of the angles of the triangle in degrees be a – d, a, a + d, where a > d> 0.
∴ a – d + a + a + d = 180°
…[Sum of the angles of a triangle is 180°]
∴ 3a = 180°
∴ a = 60° …(i)
According to the given condition, greatest angle is 5 times the smallest angle.
∴ a + d = 5 (a – d)
∴ a + d = 5a – 5d
∴ 6d = 4a
∴ 3d = 2a
∴ 3d = 2(60°) …[From (i)]
![]()
∴ The measures of the angles in degrees are
a – d = 60° – 40° = 20°
a = 60° and
a + d = 60° + 40° = 100°
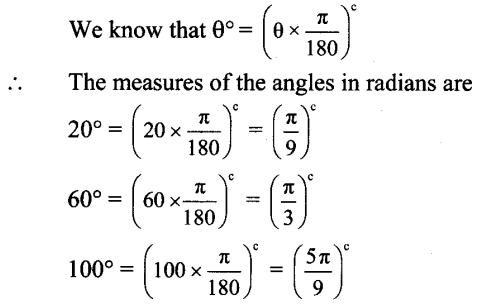
Question 11.
Solution:
Let ABCD be the cyclic quadrilateral such that
∠A = 40° and
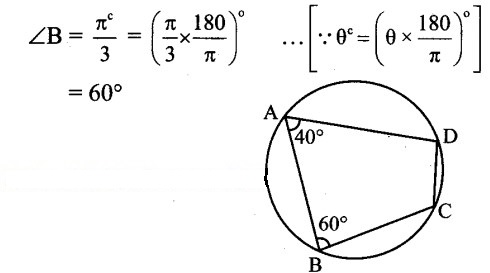
∴ ∠A + ∠C = 180°
∴ 40° + ∠C = 180°
∴ ∠C= 180°- 40°= 140°
Also, ∠B + ∠D = 180°
… [Opposite angles of a cyclic quadrilateral are supplementary]
∴ 60° + ∠D =180°
∴ ∠D = 180°- 60° = 120°
∴ The angles of the quadrilateral in degrees are 40°, 60°, 140° and 120°.
Question 12.
Solution:

Measures of other three angles are in the ratio 2:3:4.
Let the measures of the other three angles of the quadrilateral in degrees be 2k, 3k, 4k, where k is a constant.
∴ 72° + 2k + 3k + 4k = 360°
…[Sum of the angles of a quadrilateral is 360°]
∴ 9k = 288°
k = 32°
∴ The measures of the angles in degrees are
2k = 2 x 32° = 64°
3k = 3 x 32° = 96°
4k = 4 x 32°= 128°
![]()
∴ The measures of the angles in radians are
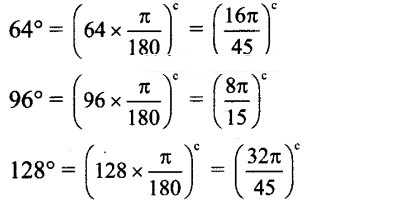
Question 13.
Find the degree and radian measures of exterior and interior angles of a regular
i. pentagon
ii. hexagon
iii. septagon
iv. octagon
Solution:
i. Pentagon:
Number of sides = 5
Number of exterior angles = 5
Sum of exterior angles = 360°
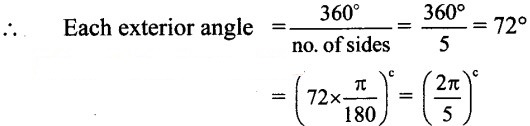
Interior angle + Exterior angle = 180°
∴ Each interior angle = 180° — 72° = 108°
= \(
ii. Hexagon:
Number of sides = 6
Number of exterior angles = 6
Sum of exterior angles = 360°
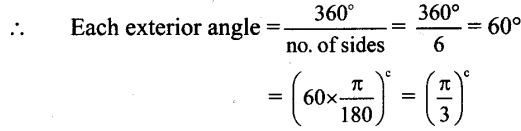
Interior angle + Exterior angle = 180°
∴ Each interior angle = 180° – 60° = 120°
= (120 x
[latex]\frac{\pi}{180}\))c = ( \(\frac{2 \pi}{3}[latex])c
iii. Septagon:
Number of sides = 7
Number of exterior angles = 7
Sum of exterior angles = 360°
∴ Each exterior angle = [latex]\frac{360^{\circ}}{\text { no. of sides }}=\frac{360^{\circ}}{7}\)
= (51.43)°
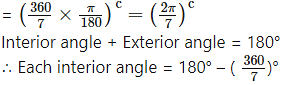

iv. Octagon:
Number of sides = 8
Number of exterior angles = 8
Sum of exterior angles = 360°
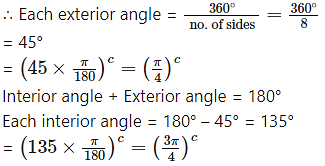
Question 14.
Find the angle between hour-hand and minute-hand in a clock at
i. ten past eleven
ii. twenty past seven
iii. thirty five past one
iv. quarter to six
v. 2:20
vi. 10:10
Solution:
i. At 11:10, the minute-hand is at mark 2 and hour-hand has crossed of the angle between 11 and 12.
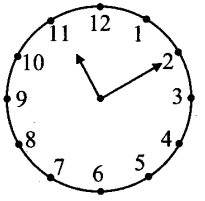

Angle between marks 11 and 2 = 3 x 30° = 90°
∴ Angle between two hands of the clock at ten past eleven = 90° – 5° = 85°
ii. At 7 : 20 the minute -hand is at mark 4 and hour -hand has crossed ()rd of angle between 7 and 8.
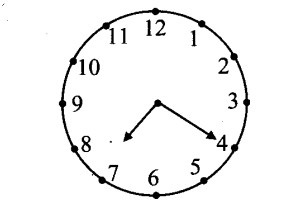
Angle between two consecutive marks
= 360°/12 = 30°
Angle traced by hour-hand in 20 minutes
= (30°)= 10°
Angle between marks 4 and 7 = 3 x 30° = 90°
Angle between two hands of the clock at twenty past seven = 90° – 10° = 100°
iii. At 1 : 35 the minute -hand is at mark 7 and hour -hand has crossed ()th of angle between 1 and 2.
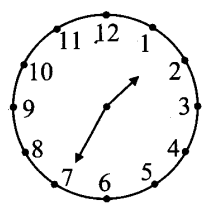
Angle between two consecutive marks
= 360°/12 = 30°
Angle traced by hour-hand in 35 minutes
![]()
Angle between marks 1 and 7 = 6 x 30° = 180°

iv. At 5:45, the minute-hand is at mark 9 and hour- hand has crossed ( frac34 )th of the angle between 5 and 6.
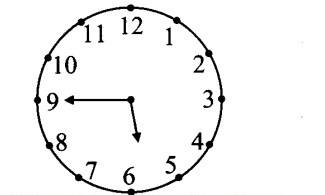
Angle between two consecutive marks
= 360°/12 = 30°
Angle traced by hour-hand in 45 minutes
![]()
Angle between marks 5 and 9
= 4 x 30° = 120°
![]()
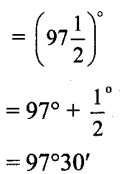
v. At 2 : 20, the minute-hand is at mark 4 hour hand has crossed 1/3rd of the angle between 2 and 3.
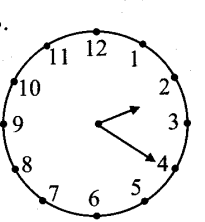
Angle between two consecutive marks = 360°/12 = 30°
Angle traced by hour-hand in 20 minutes
= frac13(30°)= 10°
Angle between marks 2 and 4 = 2 x 30° = 60°
∴ Angle between two hands of the clock at 2 :20 = 60° – 10° = 50°
.vi. At 10:10, the minute-hand is at mark 2 and hour-hand has crossed\frac{1}{6}[/latex]
th between 10 and 11.
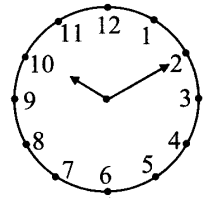
Angle between two consecutive marks
360°/12 = 30°
Angle traced by hour-hand in 10 minutes
=1/6 (30°) = 5°
Angle between marks 10 and 2= 4 x 30° = 120°
… Angle between two hands of the clock at 10:10
= 120° – 5°= 115°