Chapter 1 Complex Numbers Ex 1.2
Chapter 1 Complex Numbers Ex 1.2
Question 1.
Find the square root of the following complex numbers:
(i) -8 – 6i
Solution:
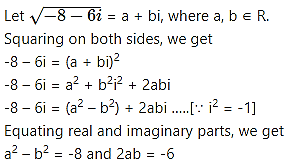
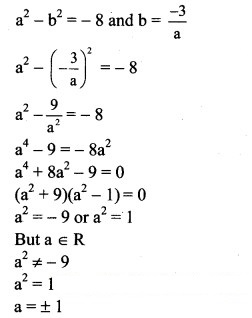

(ii) 7 + 24i
Solution:
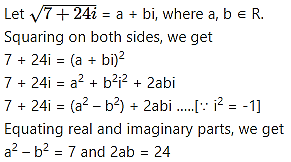
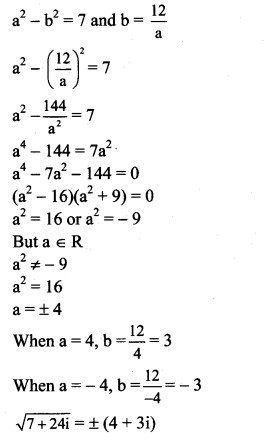
(iii) 1 + 4√3 i
Solution:



(iv) 3 + 2√10 i
Solution:



(v) 2(1 – √3 i)
Solution:
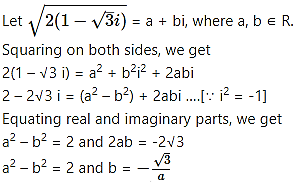

Question 2.
Solve the following quadratic equations:
(i) 8 + 2x + 1 = 0
Solution:
Given equation is 8 + 2x + 1 = 0
Comparing with a + bx + c = 0, we get
a = 8, b = 2, c = 1
Discriminant = – 4ac
= (2 – 4 × 8 × 1
= 4 – 32
= -28 < 0
So, the given equation has complex roots.
These roots are given by

(ii) 2 – √3 x + 1 = 0
Solution:
Given equation is 2 – √3 x + 1 = 0
Comparing with a + bx + c = 0, we get
a = 2, b = -√3, c = 1
Discriminant = – 4ac
= (-√3 – 4 × 2 × 1
= 3 – 8
= -5 < 0
So, the given equation has complex roots.
These roots are given by
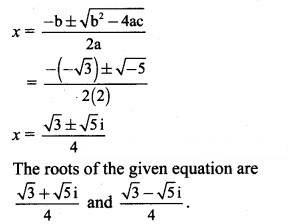
(iii) 3 – 7x + 5 = 0
Solution:
Given equation is 3 – 7x + 5 = 0
Comparing with a + bx + c = 0, we get
a = 3, b = -7, c = 5
Discriminant = – 4ac
= (-7 – 4 × 3 × 5
= 49 – 60
= -11 < 0
So, the given equation has complex roots.
These roots are given by
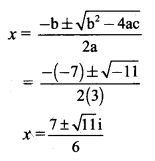
![]()
(iv) – 4x + 13 = 0
Solution:
Given equation is – 4x + 13 = 0
Comparing with a + bx + c = 0, we get
a = 1, b = -4, c = 13
Discriminant = – 4ac
= (-4 – 4 × 1 × 13
= 16 – 52
= -36 < 0
So, the given equation has complex roots.
These roots are given by

∴ The roots of the given equation are 2 + 3i and 2 – 3i.
Question 3.
Solve the following quadratic equations:
(i) + 3ix + 10 = 0
Solution:
Given equation is + 3ix + 10 = 0
Comparing with a + bx + c = 0, we get
a = 1, b = 3i, c = 10
Discriminant = – 4ac
= (3i – 4 × 1 × 10
= 9 – 40
= -9 – 40 ……[∵ = -1]
= -49 < 0
So, the given equation has complex roots.
These roots are given by
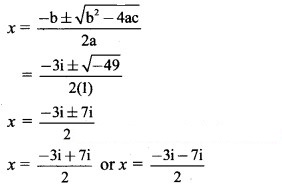
∴ x = 2i or x = -5i
∴ The roots of the given equation are 2i and -5i.
(ii) 2 + 3ix + 2 = 0
Solution:
Given equation is 2 + 3ix + 2 = 0
Comparing with ax + bx + c = 0, we get
a = 2, b = 3i, c = 2
Discriminant = – 4ac
= (3i – 4 × 2 × 2
= 9 – 16
= -9 – 16 …..[∵ = -1]
= -25 < 0
So, the given equation has complex roots.
These roots are given by

∴ The roots of the given equation are i and -2i.
(iii) + 4ix – 4 = 0
Solution:
Given equation is + 4ix – 4 = 0
Comparing with a + bx + c = 0, we get
a = 1, b = 4i, c = -4
Discriminant = – 4ac
= (4i – 4 × 1 × (-4)
= 16 + 16
= -16 + 16 …..[∵ = -1]
= 0
So, the given equation has equal roots.
These roots are given by

∴ x = -2i
∴ The root of the given equation is -2i.
(iv) i – 4x – 4i = 0
Solution:
i – 4x – 4i = 0
Multiplying throughout by i, we get
i2 – 4ix – 4 = 0
– – 4ix + 4 = 0 …[∵ = -1]
+ 4ix – 4 = 0
Comparing with a + bx + c = 0, we get
a = 1, b = 4i, c = -4
Discriminant = – 4ac
= (4i – 4 × 1 × (-4)
= 16 + 16
= -16 + 16
= 0
So, the given equation has equal roots.
These roots are given by

∴ The root of the given equation is -2i
Question 4.
Solve the following quadratic equations:
(i) – (2 + i) x – (1 – 7i) = 0
Solution:
Given equation is – (2 + i)x – (1 – 7i) = 0
Comparing with a + bx + c = 0, we get
a = 1, b = -(2 + i), c = -(1 – 7i)
Discriminant = – 4ac
= [-(2 + i) – 4 × 1 × -(1 – 7i)
= 4 + 4i + + 4 – 28i
= 4 + 4i – 1 + 4 – 28i …..[∵ = – 1]
= 7 – 24i
So, the given equation has complex roots.
These roots are given by


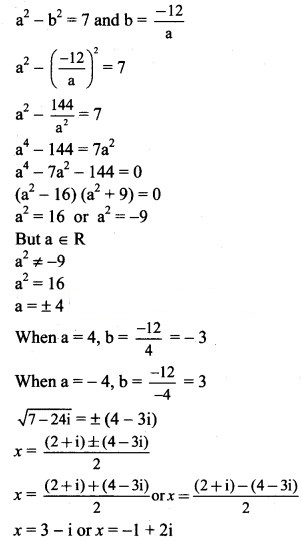

So, the given equation has complex roots.
These roots are given by

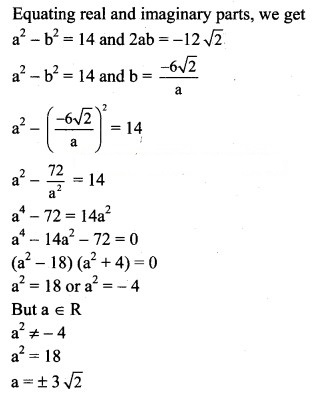

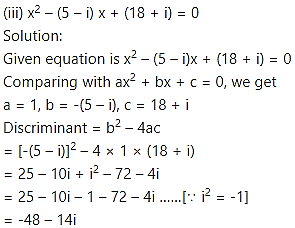
So, the given equation has complex roots.
These roots are given by
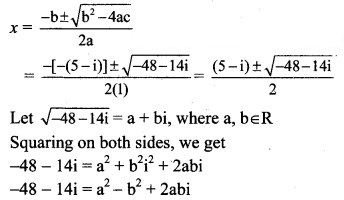
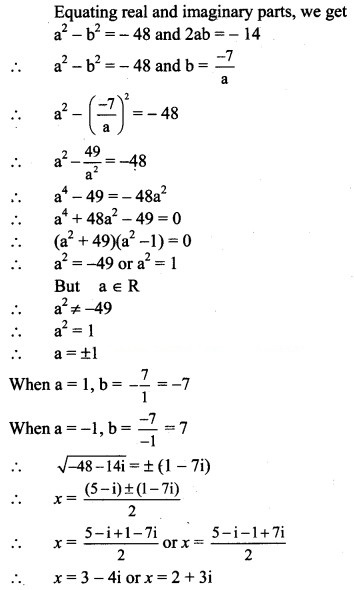

So, the given equation has complex roots.
These roots are given by

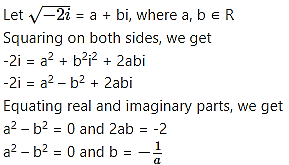
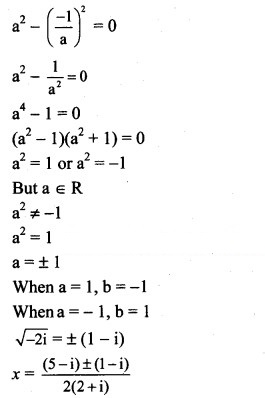
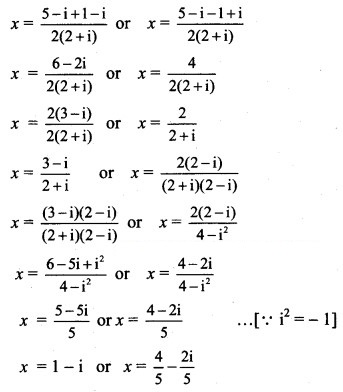
Question 5.




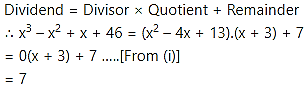
![]()
Solution:

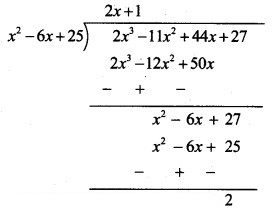
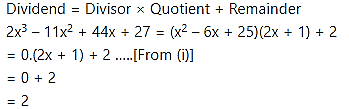
![]()
Solution:


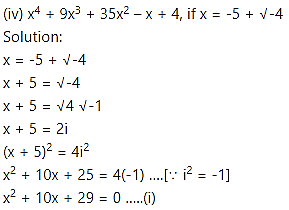

(v) 2 + 5 + 7 – x + 41, if x = -2 – √3i
Solution:

