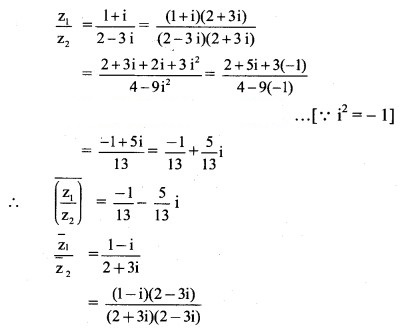Blog

Chapter 1 Complex Numbers Ex 1.3

Chapter 1 Complex Numbers Ex 1.3

Question 1.
Find the modulus and amplitude for each of the following complex numbers:
(i) 7 – 5i
Solution:
Let z = 7 – 5i
a = 7, b = -5
i.e. a > 0, b < 0

Here, (7, -5) lies in 4th quadrant.

(ii) √3 + √2 i
Solution:
Let z = √3 + √2 i
a = √3, b = √2,
i.e. a > 0, b > 0

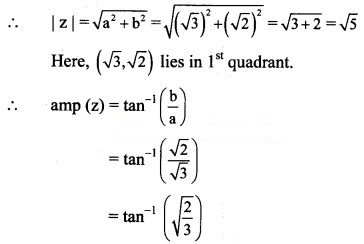
(iii) -8 + 15i
Solution:
Let z = -8 + 15i
a = -8, b = 15 , i.e. a < 0, b > 0

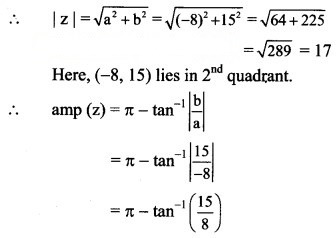
(iv) -3(1 – i)
Solution:
Let z = -3(1 – i) = -3 + 3i
a = -3, b = 3 , i.e. a < 0, b > 0

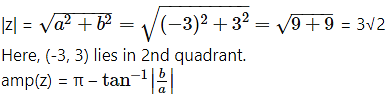
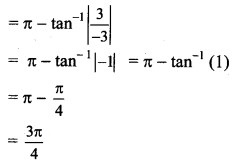
(v) -4 – 4i
Solution:
Let z = -4 – 4i
a = -4, b = -4 , i.e. a < 0, b < 0

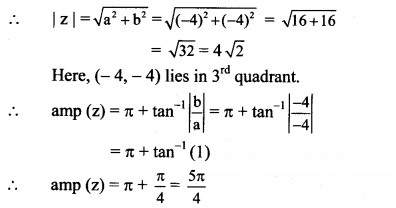
(vi) √3 – i
Solution:
Let z = √3 – i
a = √3, b = -1, i.e. a > 0, b < 0

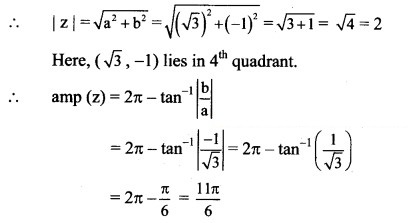
(vii) 3
Solution:
Let z = 3 + 0i
a = 3, b = 0
z is a real number, it lies on the positive real axis.

and amp (z) = 0

(viii) 1 + i
Solution:
Let z = 1 + i
a = 1, b = 1, i.e. a > 0, b > 0

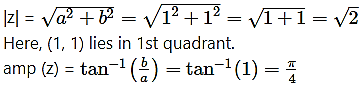
(ix) 1 + i√3
Solution:
Let z = 1 + i√3
a = 1, b = √3, i.e. a > 0, b > 0

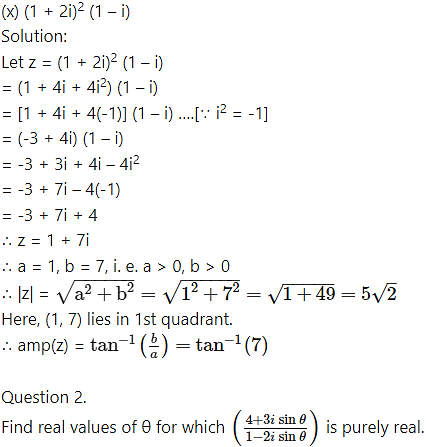
Solution:

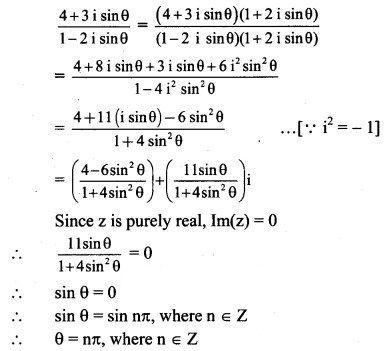
Question 3.

The above complex numbers will be represented by the points
A (3, 5), B (3, -5), C (-3, -5) , D (-3, 5) respectively as shown below:

Question 4.
Express the following complex numbers in polar form and exponential form.
(i) -1 + √3 i
Solution:
Let z = – 1 + √3
a = -1, b = √3

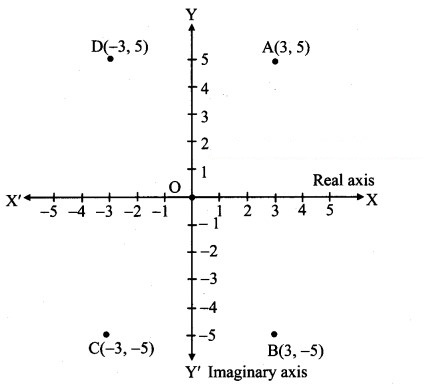
(ii) -i
Solution:
Let z = -i = 0 – i
a = 0, b = -1

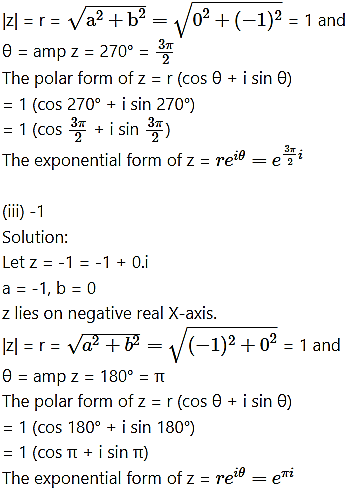
Solution:

(v) 2+2i/1-3i

Solution: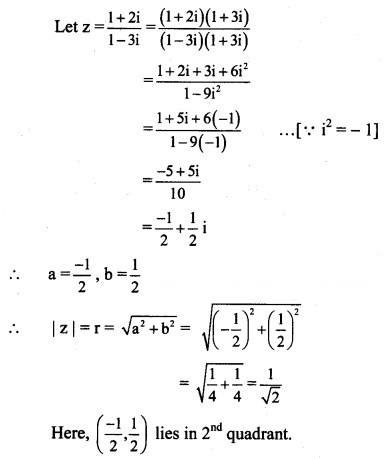

(vi) 1+7i/(2-i)²
Solution: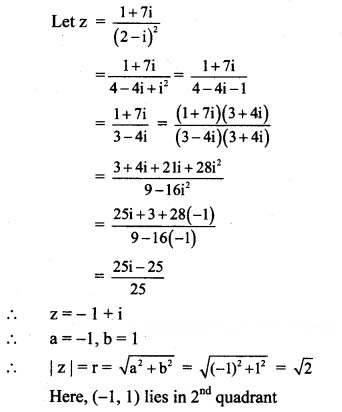

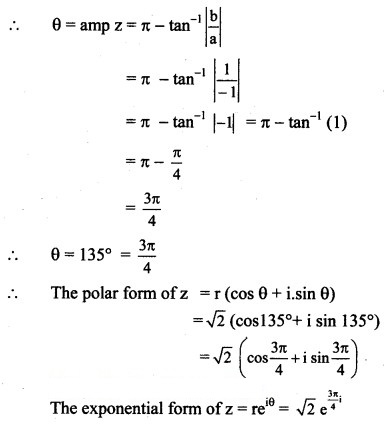
Question 5.
Express the following numbers in the form x + iy:

Solution:

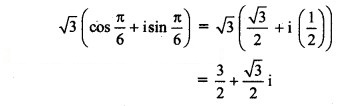
Solution:

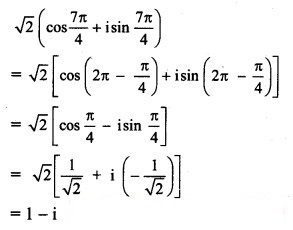
Solution:

Solution:

Solution:

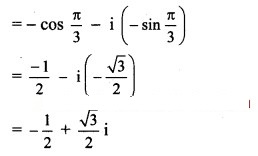
Solution:

Question 6.

Solution:

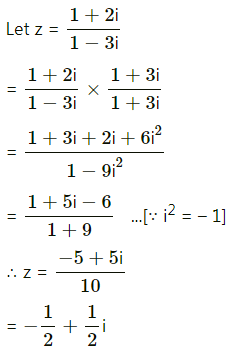
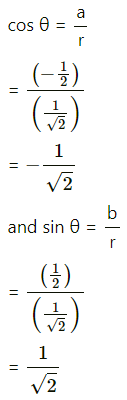
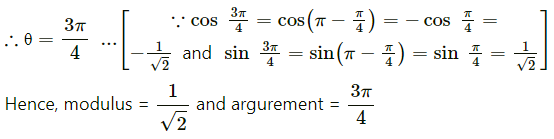
Question 7.

Solution:

Question 8.
For z = 2 + 3i, verify the following:

Solution:

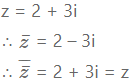
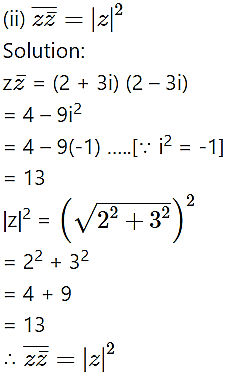
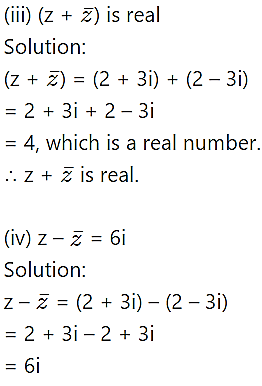
Question 9.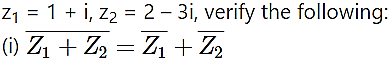

Solution:

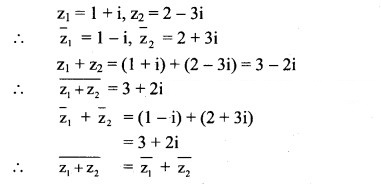
Solution:

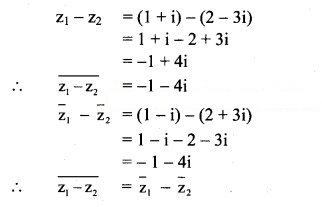
Solution:

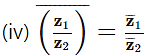
Solution: