Chapter 1 Complex Numbers Ex 1.4
Chapter 1 Complex Numbers Ex 1.4
Question 1.
Find the value of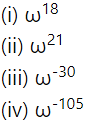
Solution:
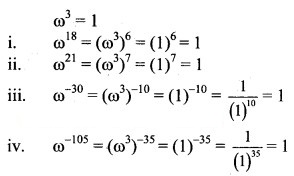
Question 2.

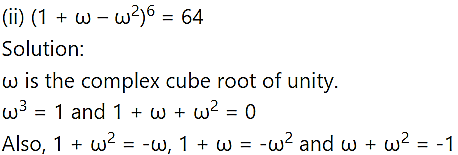
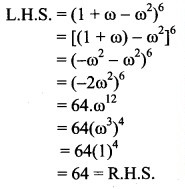
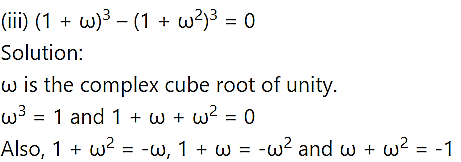
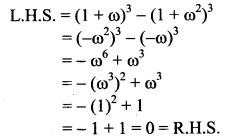
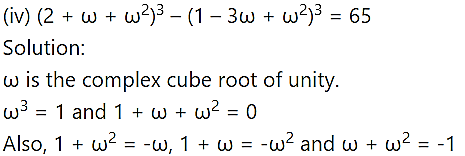
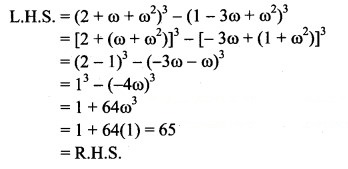
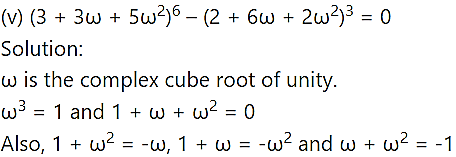
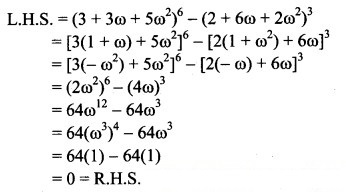
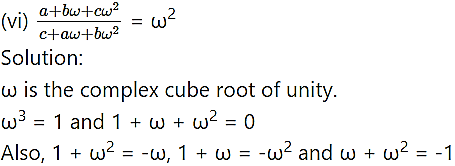
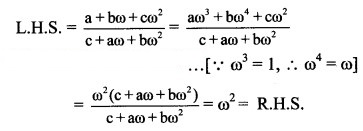
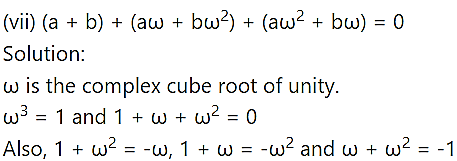
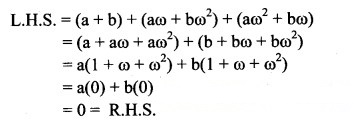
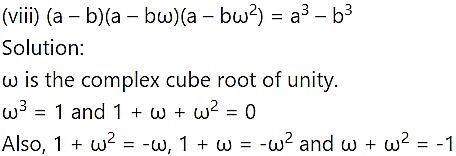
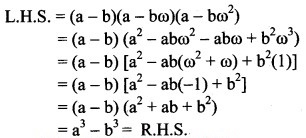
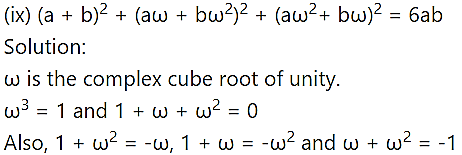
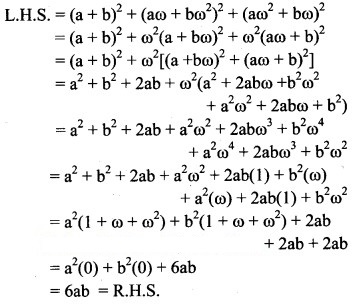
Question 3.
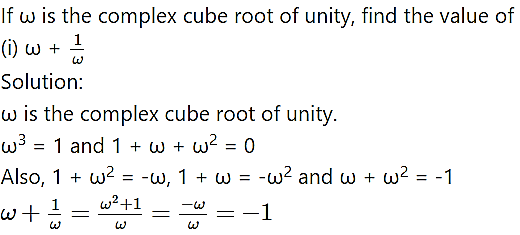
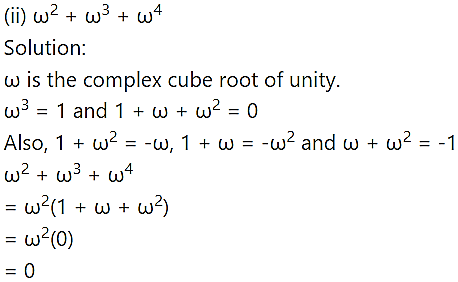
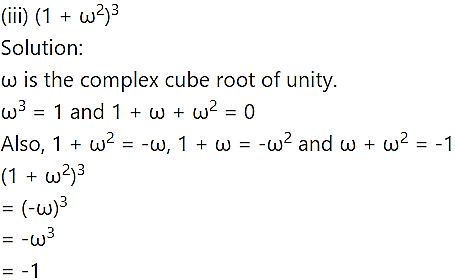
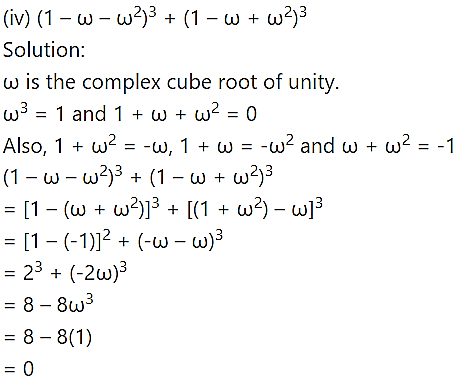
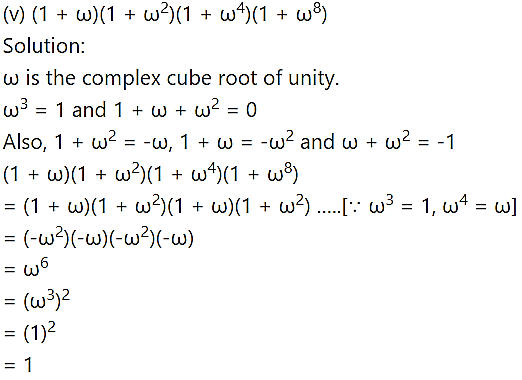
Question 4.
If α and β are the complex cube roots of unity, show that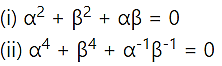
Solution:
α and β are the complex cube roots of unity.


Question 5.
If x = a + b, y = αa + βb and z = aβ + bα, where α and β are complex cube roots of unity, show that xyz = a3 + b3.
Solution:
x = a + b, y = αa + βb, z = aβ + bα
α and β are the complex cube roots of unity.
![]()
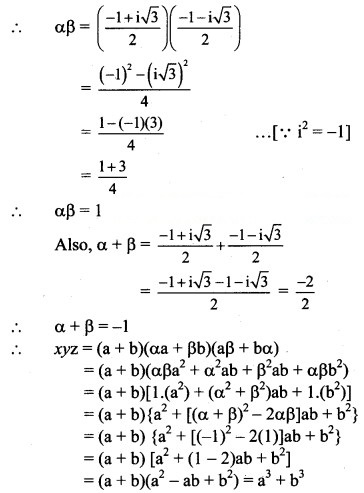
Question 6.
Find the equation in cartesian coordinates of the locus of z if
(i) |z| = 10
Solution:
Let z = x + iy
|z| = 10
|x + iy| = 10

(ii) |z – 3| = 2
Solution:
Let z = x + iy
|z – 3| = 2
|x + iy – 3| = 2
|(x – 3) + iy| = 2
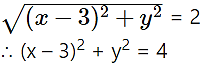
(iii) |z – 5 + 6i| = 5
Solution:
Let z = x + iy
|z – 5 + 6i| = 5
|x + iy – 5 + 6i| = 5
|(x – 5) + i(y + 6)| = 5

(iv) |z + 8| = |z – 4|
Solution:
Let z = x + iy
|z + 8| = |z – 4|
|x + iy + 8| = |x + iy – 4|
|(x + 8) + iy | = |(x – 4) + iy|

16x + 64 = -8x + 16
24x + 48 = 0
∴ x + 2 = 0
(v) |z – 2 – 2i | = |z + 2 + 2i|
Solution:
Let z = x + iy
|z – 2 – 2i| = |z + 2 + 2i|
|x + iy – 2 – 2i | = |x + iy + 2 + 2i |
|(x – 2) + i(y – 2)| = |(x + 2) + i(y + 2)|
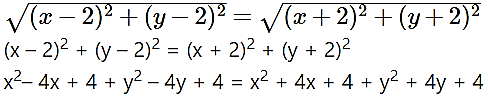
-4x – 4y = 4x + 4y
8x + 8y = 0
x + y = 0
y = -x
![]()
Solution:
Let z = x + iy
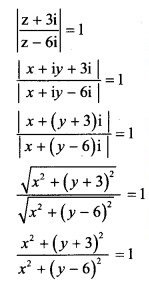
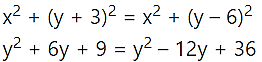
18y – 27 = 0
2y – 3 = 0
Question 7.
Use De Moivre’s theorem and simplify the following:
Solution:


![]()
Solution:
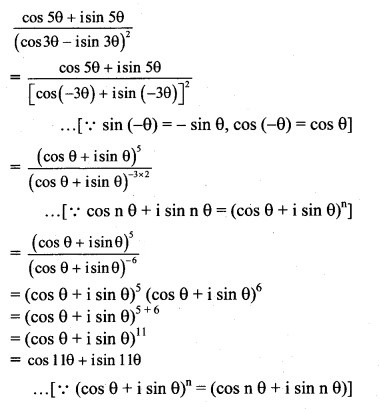
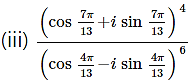
Solution:
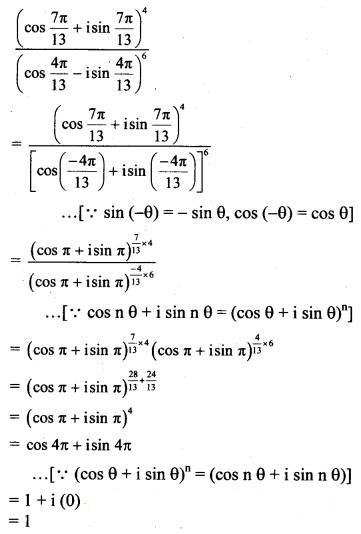
Question 8.
Express the following in the form a + ib, a, b ∈ R, using De Moivre’s theorem.
(i) (1 – i
Solution:


(ii) (1 + i
Solution:

(iii) (1 – √3 i
Solution:
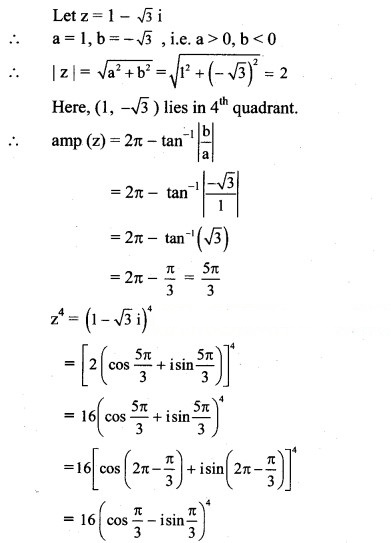
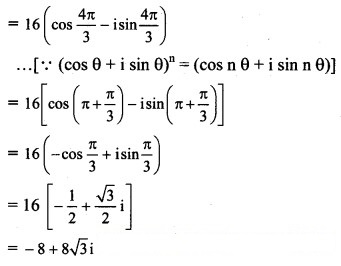
(iv) (-2√3 – 2i
Solution:

