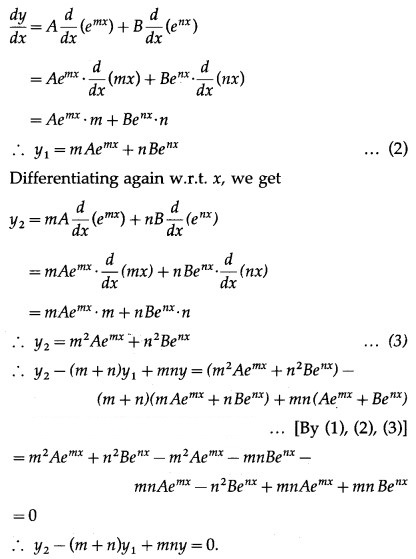Blog

Chapter 1 Differentiation Miscellaneous Exercise 1

Chapter 1 Differentiation Miscellaneous Exercise 1

(I) Choose the correct option from the given alternatives:

Question 2.

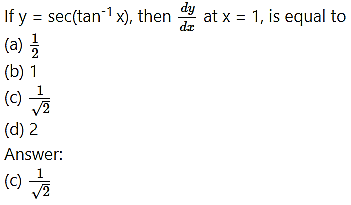
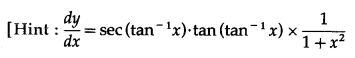
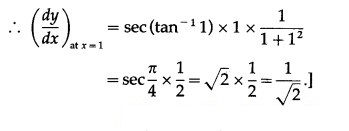
Question 3.

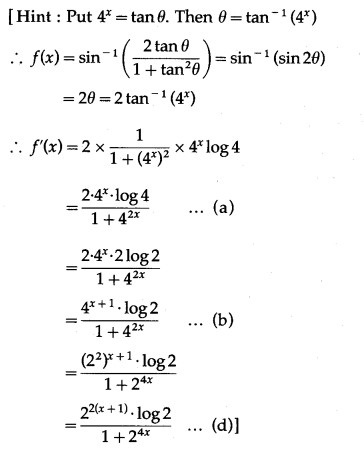
Question 4.

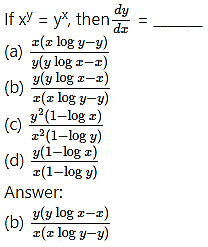
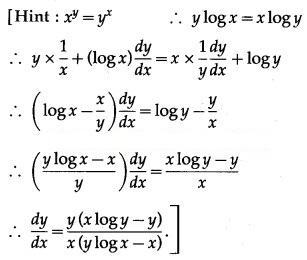
Question 5.

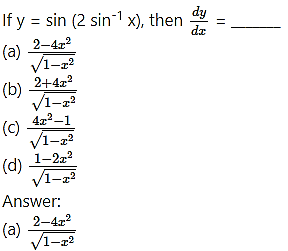
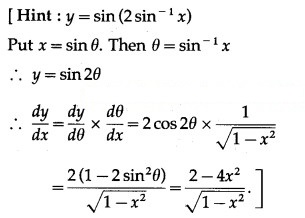
Question 6.

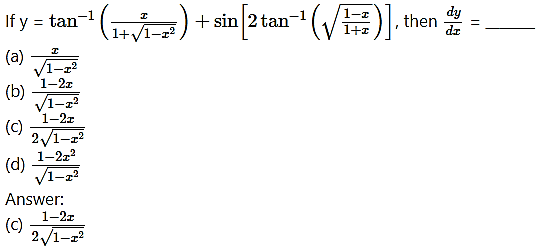
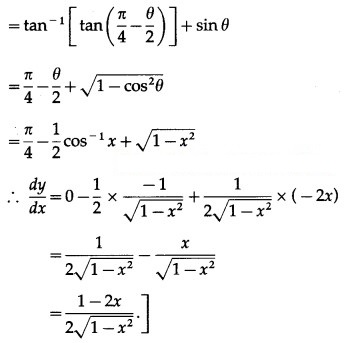
Question 7.
If y is a function of x and log(x + y) = 2xy, then the value of y'(0) = _______
(a) 2
(b) 0
(c) -1
(d) 1
Answer:
(d) 1

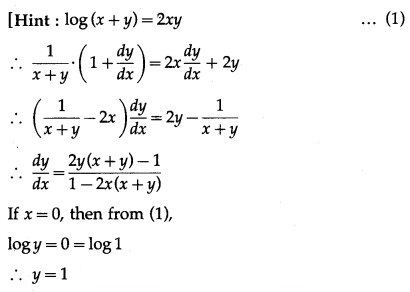
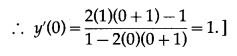
Question 8.

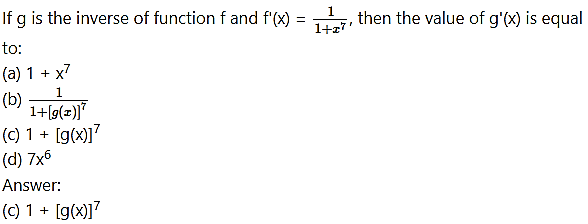
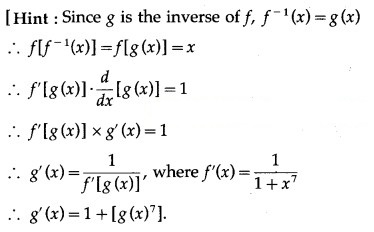
Question 9.

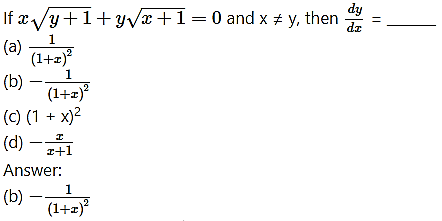
Question 10.

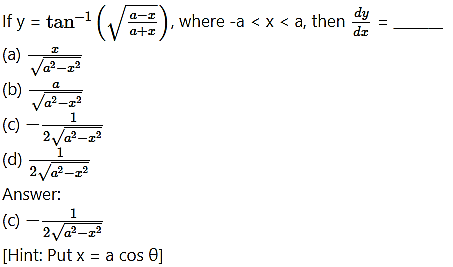
Question 11.

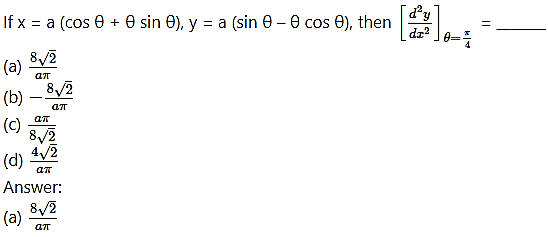
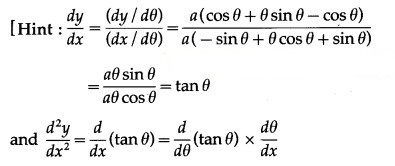
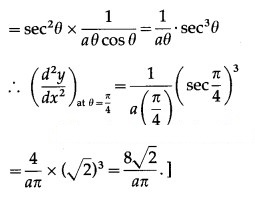
Question 12.

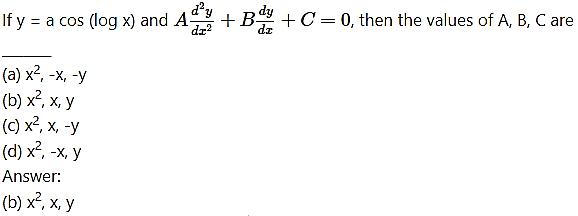
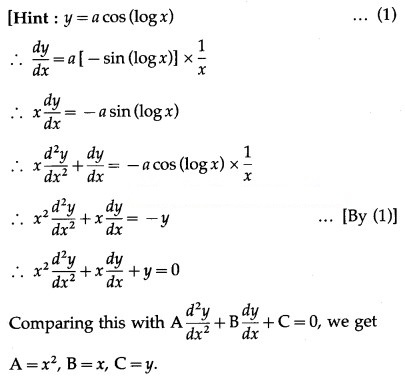
(II) Solve the following:

Question 1.


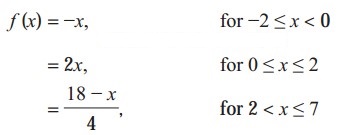
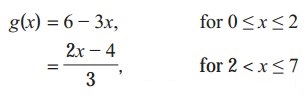
Let u(x) = f[g(x)], v(x) = g[f(x)] and w(x) = g[g(x)]. Find each derivative at x = 1, if it exists i.e. find u'(1), v'(1) and w'(1). if it doesn’t exist then explain why?
Solution:

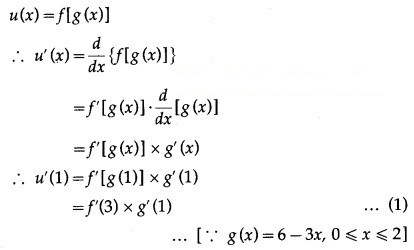
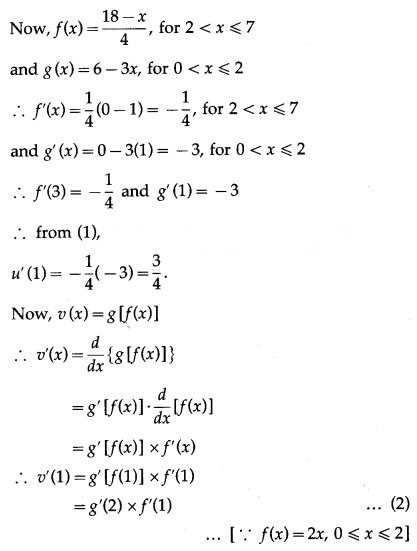
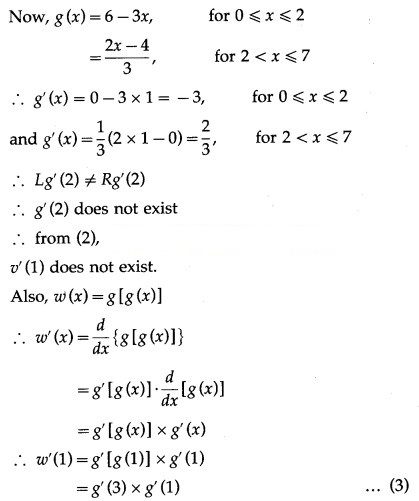
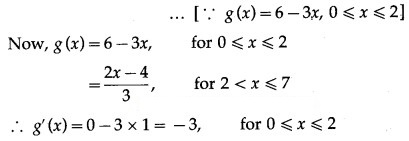
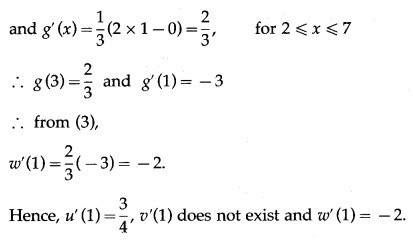
Question 2.
The values of f(x), g(x), f'(x) and g'(x) are given in the following table: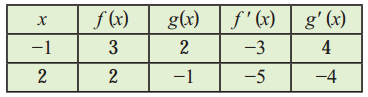

Match the following: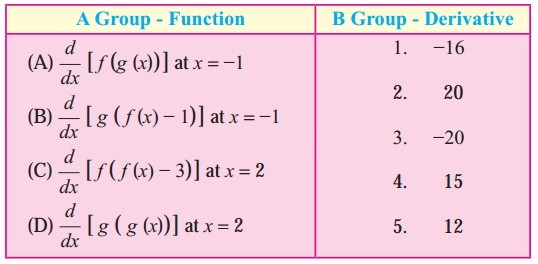

Solution:

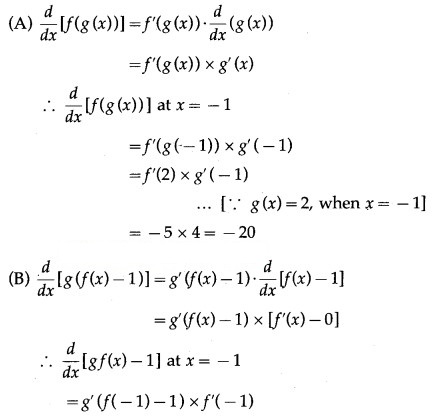
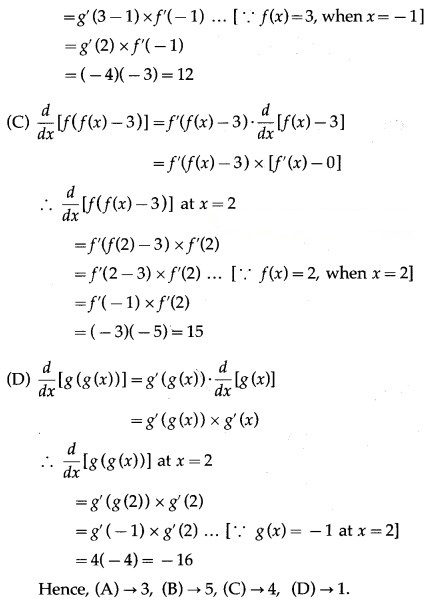
Question 3.
Suppose that the functions f and g and their derivatives with respect to x have the following values at x = 0 and x = 1.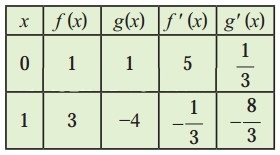


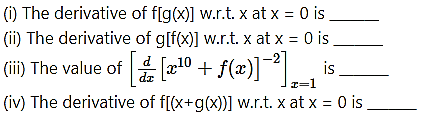
Solution:

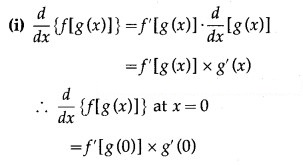
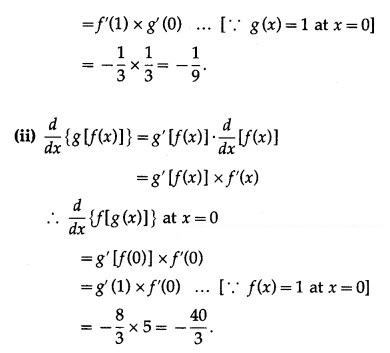
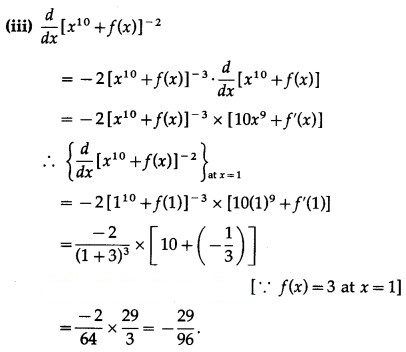
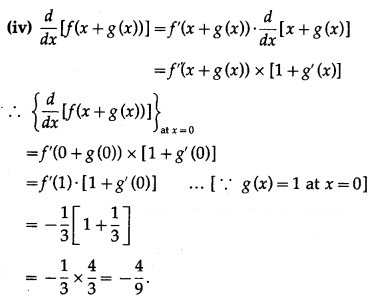
Question 4.

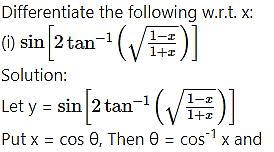
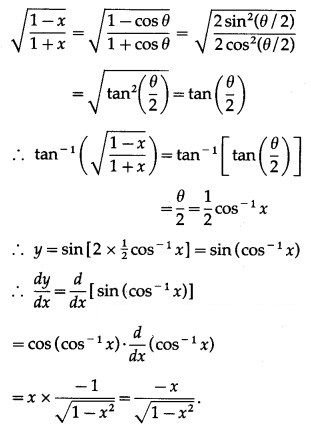
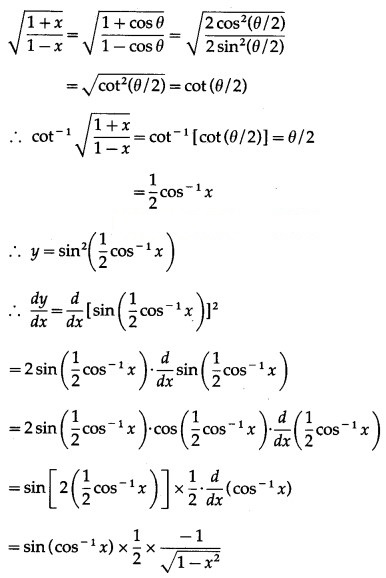
Solution:

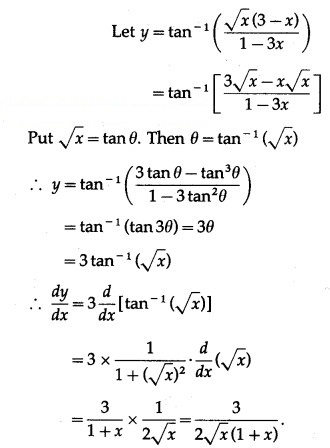
Solution:

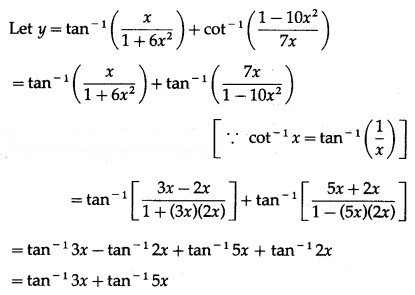
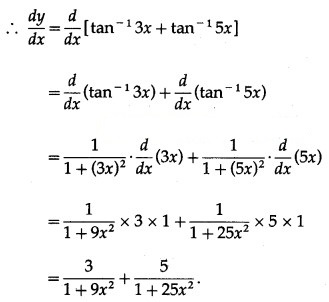
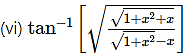
Solution:

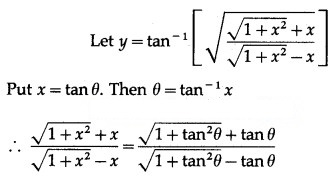
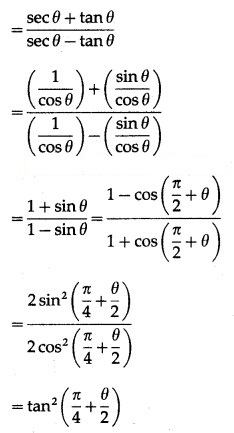
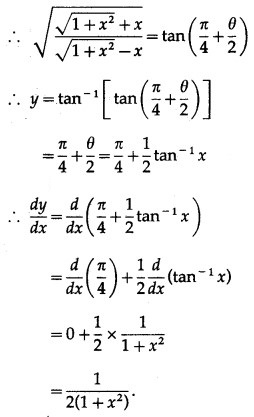
Question 5.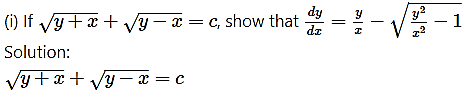

Differentiating both sides w.r.t. x, we get

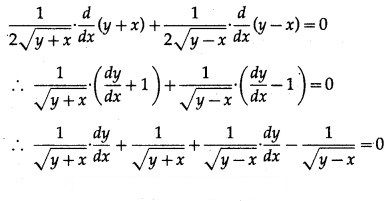
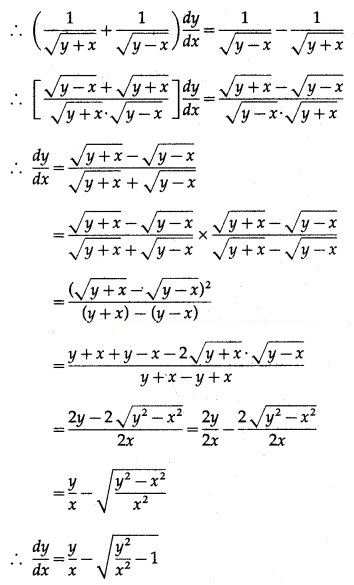
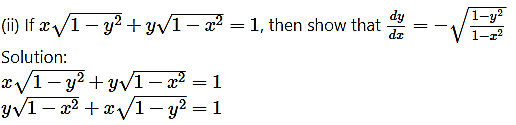
Differentiating both sides w.r.t. x, we get

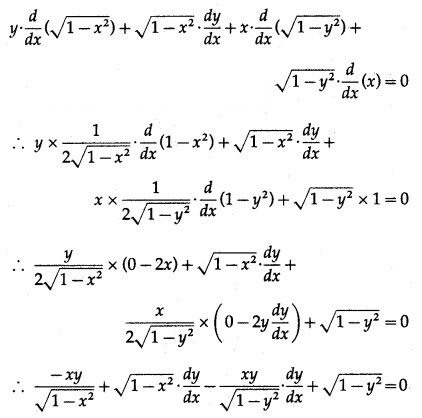
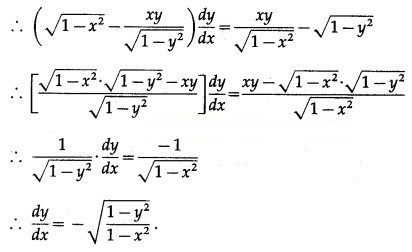
Solution:
x sin(a + y) + sin a . cos (a + y) = 0 ….. (1)
Differentiating w.r.t. x, we get

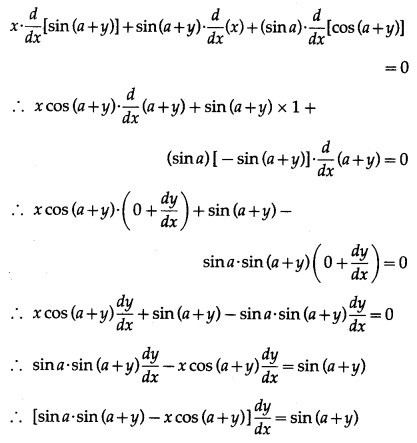
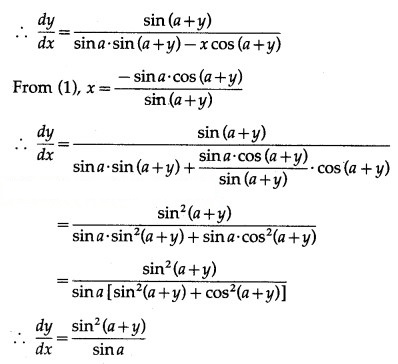
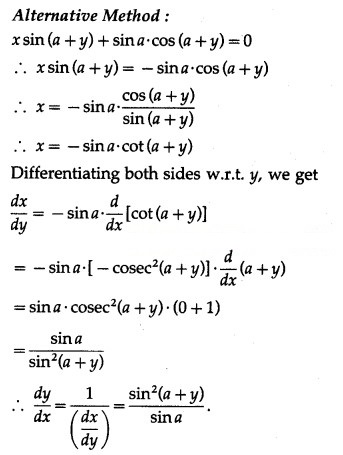
Solution:

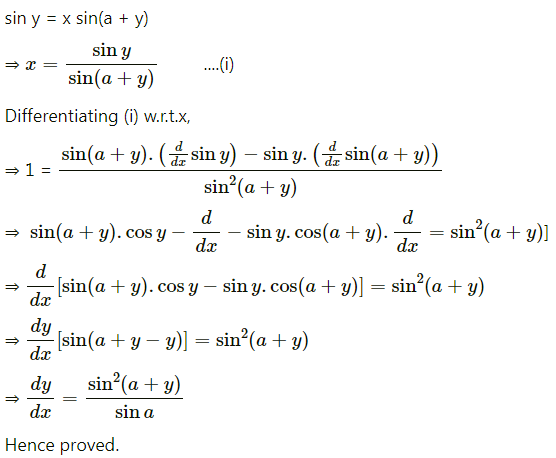
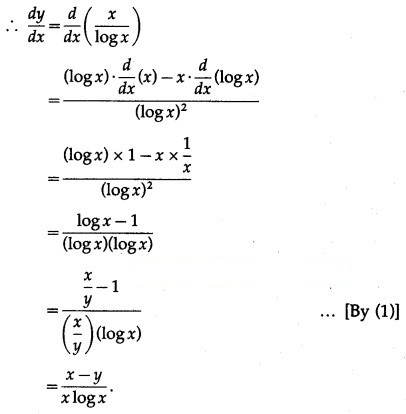
Question 6.

Solution:

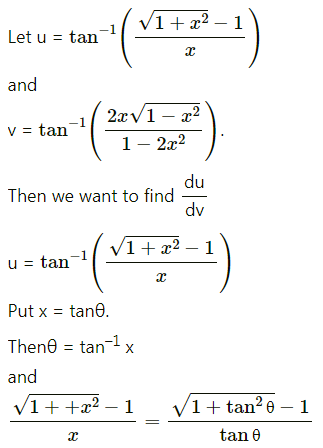
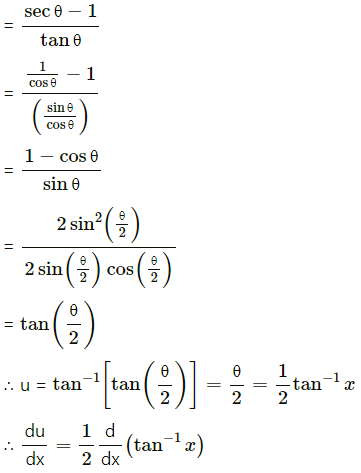
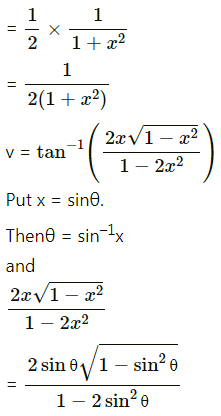
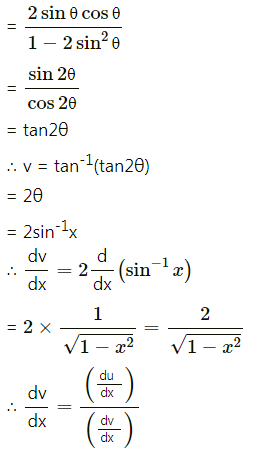
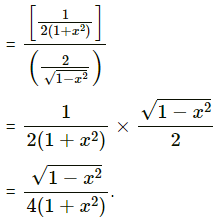
Solution:

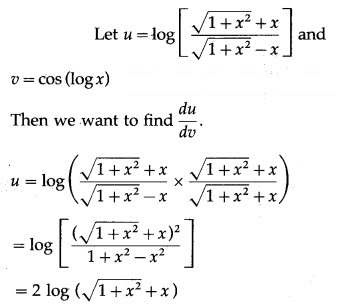
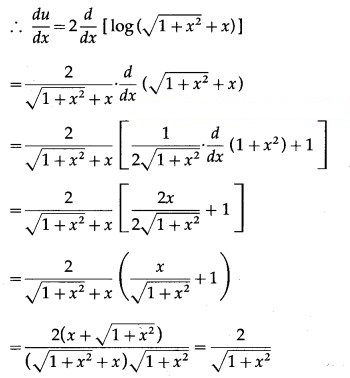
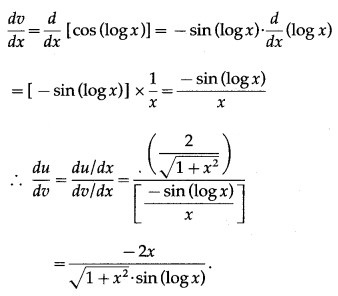
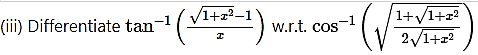
Solution:

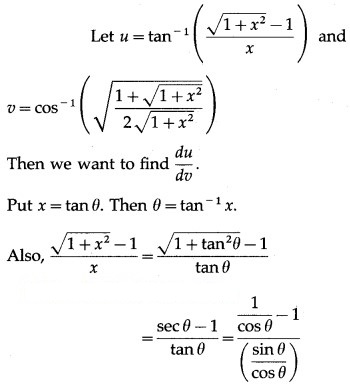
Question 7.

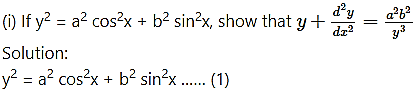
Differentiating both sides w.r.t. x, we get

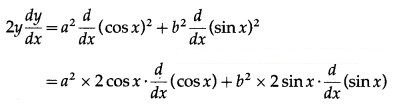
Solution:

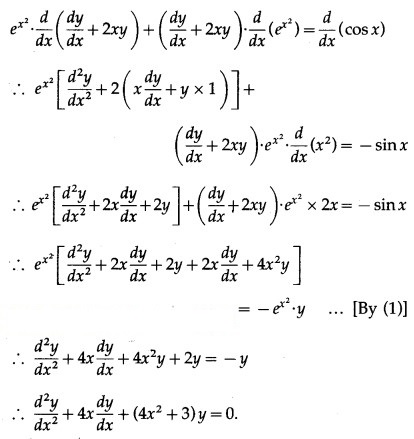
Solution:
x = a cos θ, y = b sin θ
Differentiating x and y w.r.t. θ, we get

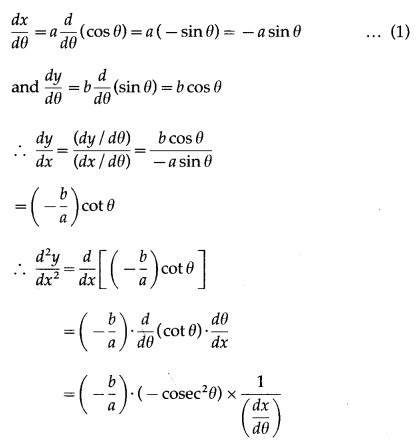
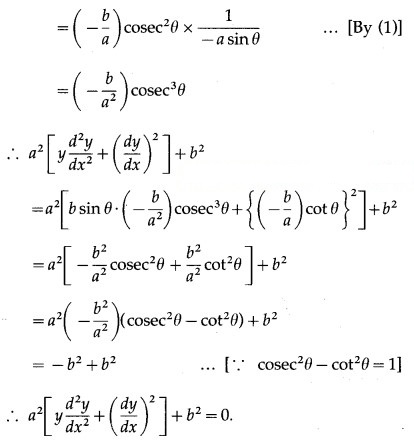
(iv) If y = A cos(log x) + B sin(log x), show that  + y = o.
Solution:
y = A cos (log x) + B sin (log x) …… (1)
Differentiating both sides w.r.t. x, we get

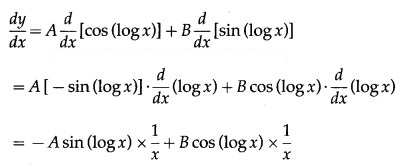
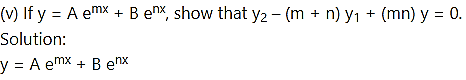
Differentiating w.r.t. x, we get