Chapter 1 Geometrical Constructions Set 1.6
Question 1.
Write the names of pairs of congruent line segments. (Use a divider to find them.)
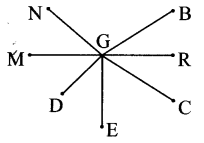
i. ___
ii. ___
iii. ___
iv. ___
Solution:
i. seg BG ≅ seg CG
ii. seg NG ≅ seg MG ≅ seg EG ≅ seg RG
Question 2.
On the line below, the distance between any two adjoining points shown on it is equal. Hence, fill in the blanks.
![]()
i. seg AB ≅ seg ___
ii. seg AP ≅ seg ___
iii. seg AC ≅ seg ___
iv. seg ___ ≅ seg BY
v. seg __ ≅ seg YQ
vi. seg BW ≅ seg ___
Solution:
i. BC
ii. QW
iii. QZ
iv. AZ
v. AY
vi. AC
Note: The above problem has many solutions. Students may write solutions other than the ones given.
Intext Questions and Activities
Question 1.
Try to draw triangles with the following data. Can you draw these triangles. If not, look for the reason why you could not draw so. (Textbook pg. no. 7)
i. ∆ABC in which m∠A = 85°, m∠B = 115°, l(AB) = 5cm.
Solution:
m∠A + m∠B = 85° + 115°
= 200°>180°
But the sum of the measures of the angles of a triangle is 180°
Hence, ∆ABC cannot be drawn.
ii. ∆PQR in which l(QR) = 2cm, l(PQ) = 4cm, l(PR) = 2cm.
Solution:
l(QR) + l(PR) = 2 cm + 2cm
= 4 cm
= l(PQ)
But in a triangle, the sum of the length of any two sides of a triangle is always greater than the length of the third side.
Hence, ∆PQR cannot be drawn.
Question 2.
Draw ∆ABC such that l(BC) = 8 cm, l(CA) = 6 cm, m∠ABC = 40°.
Draw a ray to make an angle of 40° with the base BC, l(BC) = 8 cm. We have to obtain point ‘A’ on the ray. With ‘C’ as the centre, draw an arc of radius 6 cm to do so. What do we observe? The arc intersects the ray in two different points. Thus, we get two triangles of two different shapes having the given measures. (Textbook pg. no. 7)
Solution:
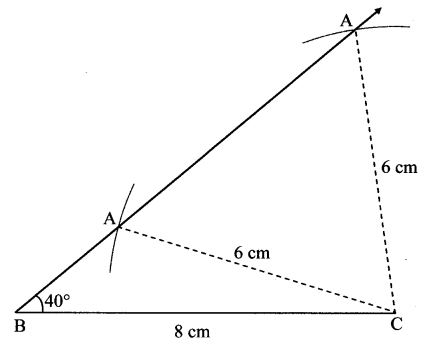
Here ∠B is an acute angle. ∠C can be an acute angle or an obtuse angle.
Hence we get two triangles of two different shapes.
Question 3.
Can a triangle be drawn if the three angles are given, but not any side? How many such triangles can be drawn? (Textbook pg. no. 7)
Solution:
Yes a triangle can be drawn.
Since the length of side is not given, any length of side can be selected and then triangle can be constructed. We will get different triangles for different length of sides.
Question 4.
Using the ruler, measure the lengths of seg AB and seg PQ. Are they of same length? Trace the seg AB on a sheet of transparent paper. Now place this new segment on PQ verify that if point A is placed on point P, then B falls on Q. (Textbook pg. no. 7)
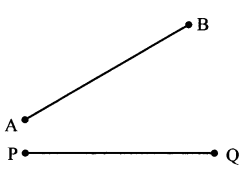
l(AB) = ___
l(PQ) = ___
Solution:
l(AB) = 4 cm
l(PQ) = 4 cm
Since the length of two segments is the same, if placed on one another, they will coincide.
Question 5.
From the shape shown below, write the names of the pairs of congruent line segments. (Textbook pg. no. 8)
i. seg AB ≅ seg DC
ii. seg AE ≅ seg BH
iii. seg EF ≅ seg ___
iv. seg DF ≅ seg ___
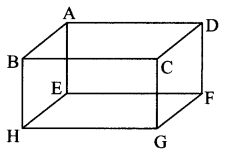
Solution:
seg EF ≅ seg AD ≅ seg BC ≅ seg HG
seg DF ≅ seg CG ≅ seg AE ≅ seg BH
Question 6.
Take a rectangular paper. Place two opposite sides upon each Other. What do you observe? (Textbook pg. no. 7)
Solution:
Opposite sides of the rectangular paper coincide and hence are congruent.
