Chapter 13 Congruence of Triangles 13.2
Question 1.
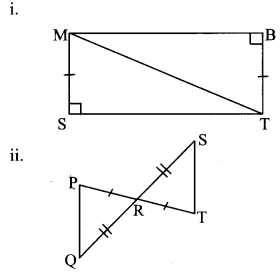
In each pair of triangles given below, parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which triangles in each pair are congruent. Also state the remaining congruent parts.
Solution:
i. In ∆MST and ∆TBM,
∴ side MS ≅ side TB … [Given]
m∠MST = m∠TBM = 90° … [Given]
hypotenuse MT ≅ hypotenuse MT
…[Common side]
∴ ∆MST ≅ ∆TBM …[by hypotenuse-side test]
∴ side ST ≅ side BM …[Corresponding sides of congruent triangles]
∠SMT ≅ ∠BTM …[Corresponding sides of congruent triangles]
∠STM ≅ ∠BMT …[Corresponding sides of congruent triangles]
ii. In ∆PRQ and ∆TRS,
side PR ≅ side TR … [Given]
∠PRQ ≅ ∠TRS …[Vertically opposite angles]
side RQ ≅ side RS … [Given]
∴ ∆PRQ ≅ ∆TRS …[by SAS test]
∴ side PQ ≅ side TS …[Corresponding sides of congruent triangles]
∠RPQ ≅ ∠RTS …[Corresponding sides of congruent triangles]
∠PQR ≅ ∠TSR …[Corresponding sides of congruent triangles]
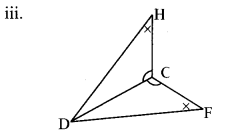
iii. In ∆DCH and ∆DCF,
∠DCH ≅ ∠DCF …[Given]
∠DHC ≅ ∠DFC …[Given]
side DC ≅ side DC …[Common side]
∴ ∆DCH ≅ ∆DCF …[by AAS test]
∴ side HC ≅ side FC …[Corresponding sides of congruent triangles]
side DH ≅ side DF…[Corresponding sides of congruent triangles]
∠HDC ≅ ∠FDC ….[Corresponding sides of congruent triangles]
Question 2.
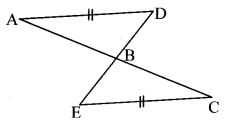
In the given figure, seg AD ≅ seg EC. Which additional information is needed to show that ∆ABD and ∆EBC will be congruent by AAS test?
Solution:
In ∆ABD and ∆CBE,
∴ seg AD ≅ seg CE …[Given]
∠ABD ≅ ∠CBE …[Vertically opposite angles]
∴ The necessary condition for the two triangles to be congruent by AAS test is
∠ADB ≅ ∠CEB, or
∠DAB ≅ ∠ECB
Intext Questions and Activities
Question 1.
Draw ∆ABC and ∆LMN such that two pairs of their sides and the angles included by them are congruent.
Draw ∆ABC and ∆LMN, l(AB) = l(LM), l(BC) = l(MN), m∠ABC = m∠LMN.
Copy ∆ABC on a tracing paper. Place the paper on ∆LMN in such a way that point A coincides with point L, side AB overlaps side LM. What do you notice?(Textbook pg. no. 83)

Solution:
We notice that ∆ABC ≅ ∆LMN.
Question 2.
Draw ∆PQR and ∆XYZ such that l(PQ) = l(X Y), l(Q R) = l(YZ), l(RP) = l(ZX). Copy ∆PQR on a tracing paper. Place it on ∆XYZ observing the correspondence P ↔ X, Q ↔ Y, R ↔ Z. What do you notice? (Textbook pg. no. 84)
Solution:
We notice that ∆PQR ≅ ∆XYZ.
Question 3.
Draw ∆XYZ and ∆DEF such that, l(XZ) = l(DF), ∠X ≅ ∠D and ∠Z ≅ ∠F.
Copy ∆XYZ on a tracing paper and place it over ∆DEF. What do you notice?(Textbook pg. no. 84)
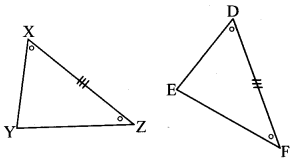
Solution:
We notice that ∆XYZ ≅ ∆DEF in the correspondence X ↔ D, Y ↔ E, Z ↔ F.
Question 4.
Draw two right angled triangles such that a side and the hypotenuse of one is congruent with the corresponding parts of the other. Copy one triangle on tracing paper and place it over the other. What do you notice? (Textbook pg. no. 84)
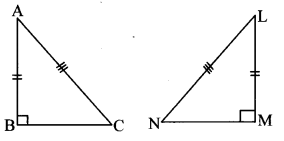
Solution:
We notice that the two triangles are congruent.
(Students should draw figures and verify the answers.)