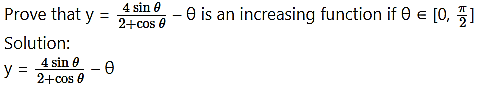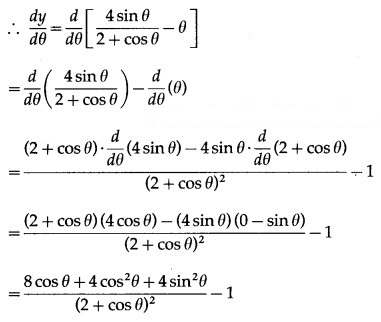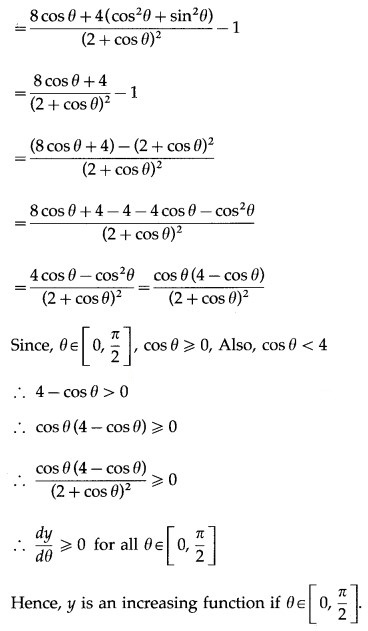Chapter 2 Applications of Derivatives Ex 2.4
Chapter 2 Applications of Derivatives Ex 2.4
Question 1.
Test whether the following functions are increasing or decreasing.
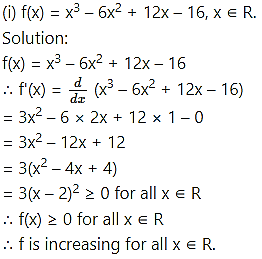
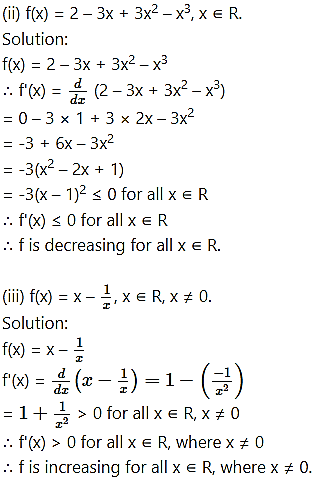
Question 2.
Find the values of x for which the following functions are strictly increasing:
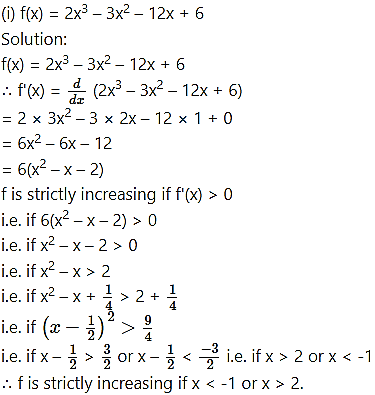
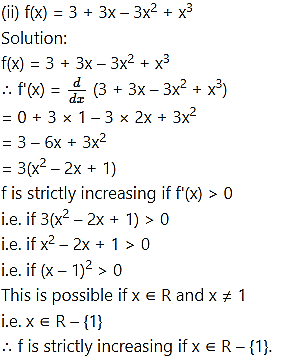
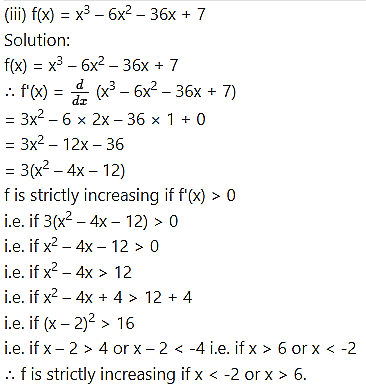
Question 3.
Find the values of x for which the following functions are strictly decreasiong:
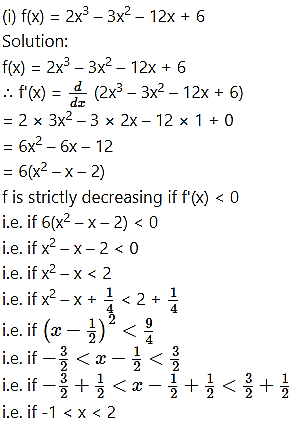
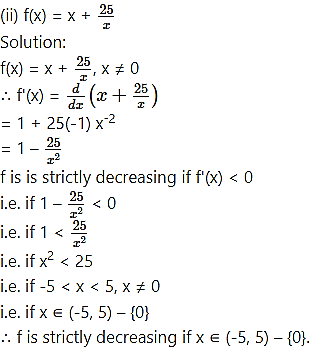
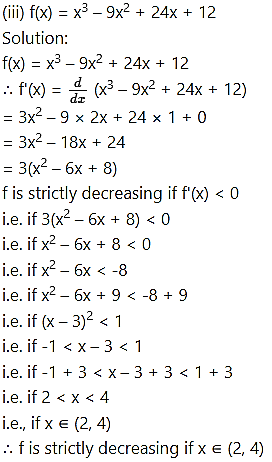
Question 4.
Find the values of x for which the function f(x) = x3 – 12x2 – 144x + 13
(a) increasing
(b) decreasing.
Solution:
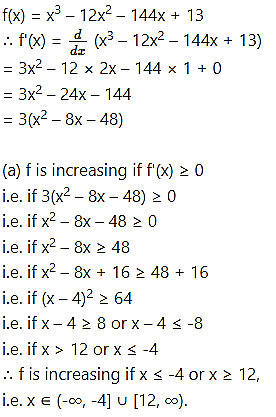
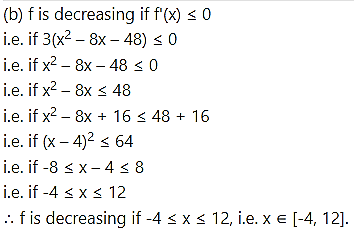
Question 5.
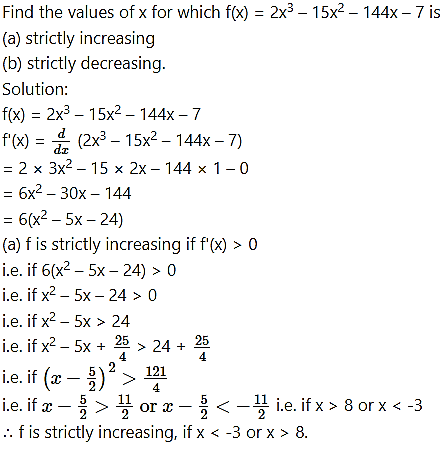
Question 6.
(a) strictly increasing
(b) strictly decreasing.
Solution:
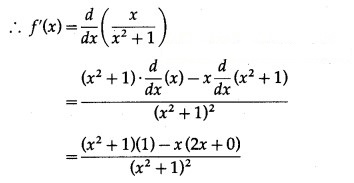
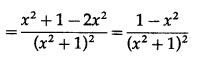
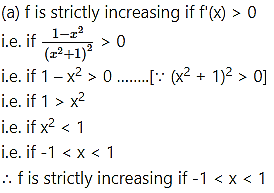
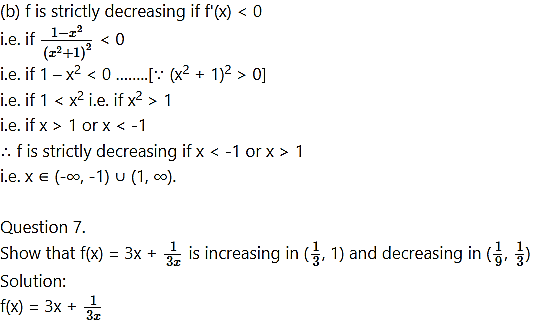
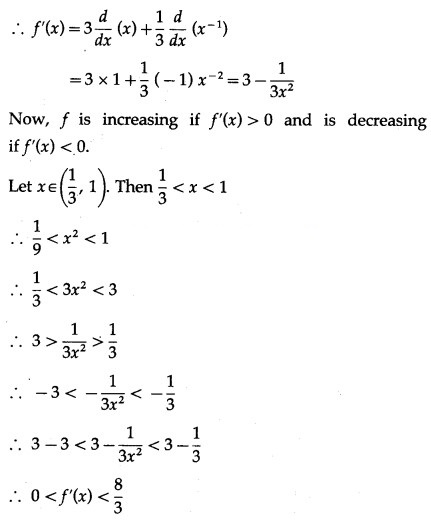
Question 8.
Show that f(x) = x – cos x is increasing for all x.
Solution:
f(x) = x – cos x
∴ f'(x) = d/dx (x – cos x)
= 1 – (-sin x)
= 1 + sin x
Now, -1 ≤ sin x ≤ 1 for all x ∈ R
∴ -1 + 1 ≤ 1 + sin x ≤ 1 for all x ∈ R
∴ 0 ≤ f'(x) ≤ 1 for all x ∈ R
∴ f'(x) ≥ 0 for all x ∈ R
∴ f is increasing for all x.
Question 9.
Find the maximum and minimum of the following functions:
Solution:
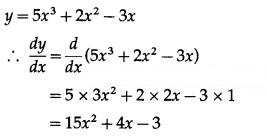
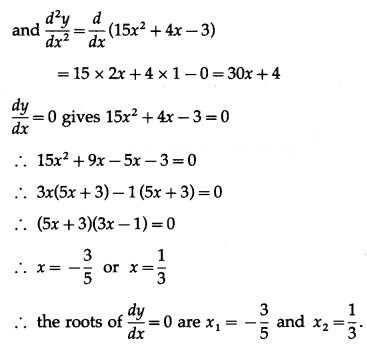
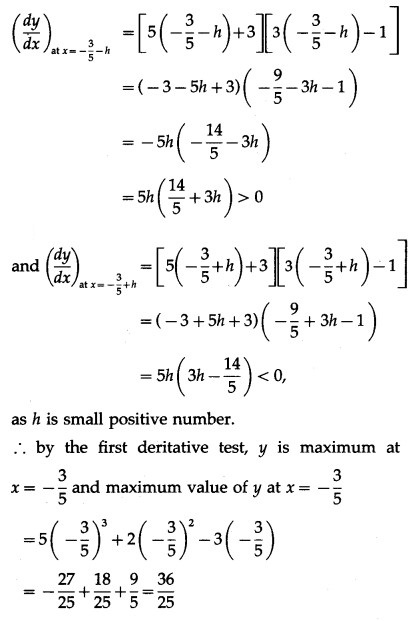
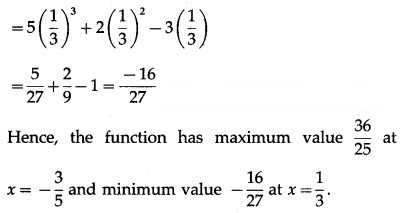
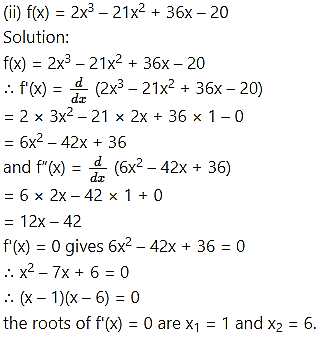
Method 1 (Second Derivative Test):
(a) f”(1) = 12(1) – 42 = -30 < 0
∴ by the second derivative test, f has maximum at x = 1
and maximum value of f at x = 1
f(1) = 2(1 – 21(1 + 36(1) – 20
= 2 – 21 + 36 – 20
= -3
(b) f”(6) = 12(6) – 42 = 30 > 0
∴ by the second derivative test, f has minimum at x = 6
and minimum value of f at x = 6
f(6) = 2(6 – 21(6 + 36(6) – 20
= 432 – 756 + 216 – 20
= -128.
Hence, the function f has maximum value -3 at x = 1 and minimum value -128 at x = 6.
Method 2 (First Derivative Test):
(a) f'(x) = 6(x – 1)(x – 6)
Consider x = 1
Let h be a small positive number. Then
f'(1 – h) = 6(1 – h – 1)(1 – h – 6)
= 6(-h)(-5 – h)
= 6h(5 + h)> 0
and f'(1 + h) = 6(1 + h – 1)(1 + h – 6)
= 6h(h – 5) < 0, as h is small positive number.
∴ by the first derivative test, f has maximum at x = 1 and maximum value of f at x = 1
f(1) = 2(1 – 21(1 + 36(1) – 20
= 2 – 21 + 36 – 20
= -3
(b) f'(x) = 6(x – 1)(x – 6)
Consider x = 6
Let h be a small positive number. Then
f'(6 – h) = 6(6 – h – 1)(6 – h – 6)
= 6(5 – h)(-h)
= -6h(5 – h) < 0, as h is small positive number
and f'(6 + h) = 6(6 + h – 1)(6 + h – 6) = 6(5 + h)(h) > 0
∴ by the first derivative test, f has minimum at x = 6
and minimum value of f at x = 6
f(6) = 2(6 – 21(6 + 36(6) – 20
= 432 – 756 + 216 – 20
= -128
Hence, the function f has maximum value -3 at x = 1
and minimum value -128 at x = 6.
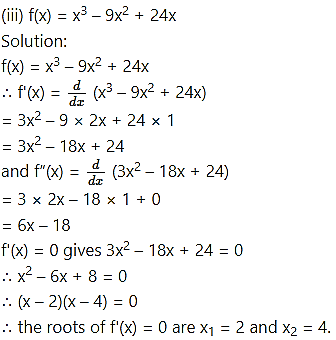
(a) f”(2) = 6(2) – 18 = -6 < 0
∴ by the second derivative test, f has maximum at x = 2
and maximum value of f at x = 2
f(2) = (2 – 9(2 + 24(2)
= 8 – 36 + 48
= 20
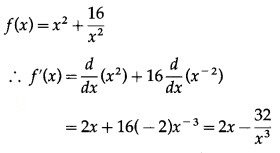
(v) f(x) = x log x
Solution:
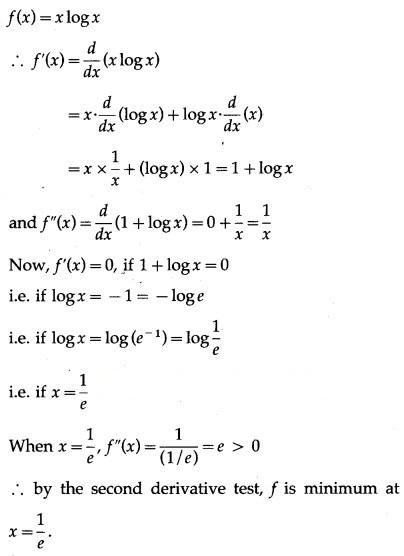
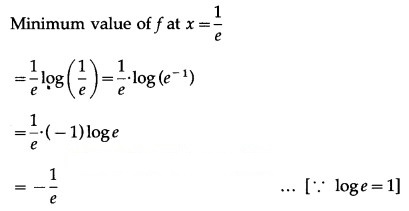
Solution:
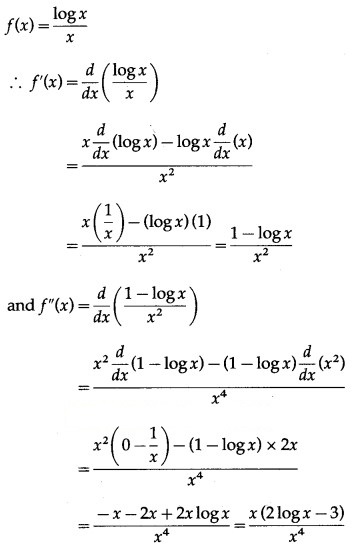
Question 10.
Divide the number 30 into two parts such that their product is maximum.
Solution:
Let the first part of 30 be x.
Then the second part is 30 – x.
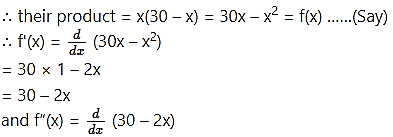
= 0 – 2 × 1
= -2
The root of the equation f(x) = 0,
i.e. 30 – 2x = 0 is x = 15 and f”(15) = -2 < 0
∴ by the second derivative test, f is maximum at x = 15.
Hence, the required parts of 30 are 15 and 15.
Question 11.
Divide the number 20 into two parts such that the sum of their squares is minimum.
Solution:
Let the first part of 20 be x.
Then the second part is 20 – x.
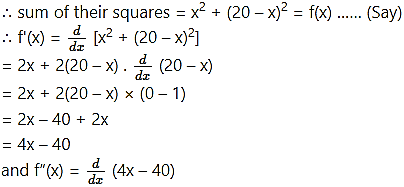
= 4 × 1 – 0
= 4
The root of the equation f'(x) = 0,
i.e. 4x – 40 = 0 is x = 10 and f”(10) = 4 > 0
∴ by the second derivative test, f is minimum at x = 10.
Hence, the required parts of 20 are 10 and 10.
Question 12.
A wire of length 36 meters is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum.
Solution:
Let x metres and y metres be the length and breadth of the rectangle.
Then its perimeter is 2(x + y) = 36
x + y = 18
y = 18 – x
Area of the rectangle = xy = x (18 – x)
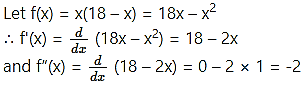
Now, f'(x) = 0, if 18 – 2x = 0
i.e. if x = 9
and f”(9) = -2 < 0
∴ by the second derivative test, f has maximum value at x = 9.
When x = 9, y = 18 – 9 = 9
∴ x = 9 cm, y = 9 cm
∴ the rectangle is a square of side 9 metres.
Question 13.
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – . Find the maximum height it can reach.
Solution:
The height h at any t is given by h = 3 + 14t – 5
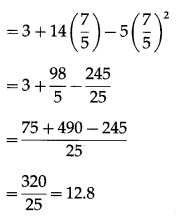
Hence, the maximum height the ball can reach = 12.8 units.
Question 14.
Find the largest size of a rectangle that can be inscribed in a semicircle of radius 1 unit, so that two vertices lie on the diameter.
Solution:
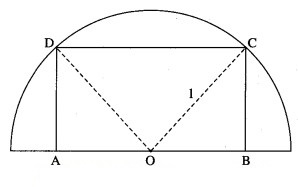
Let ABCD be the rectangle inscribed in a semicircle of radius 1 unit such that the vertices A and B lie on the diameter.
Let AB = DC = x and BC = AD = y.
Let O be the centre of the semicircle.
Join OC and OD. Then OC = OD = radius = 1.
Also, AD = BC and m∠A = m∠B = 90°.
∴ OA = OB
In right angled triangle OBC,
O + B = O
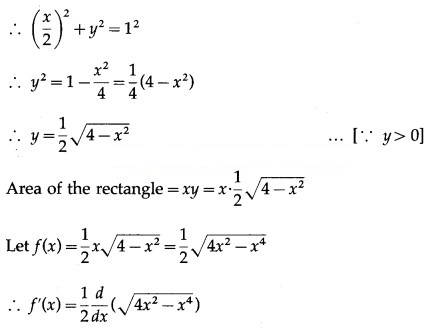
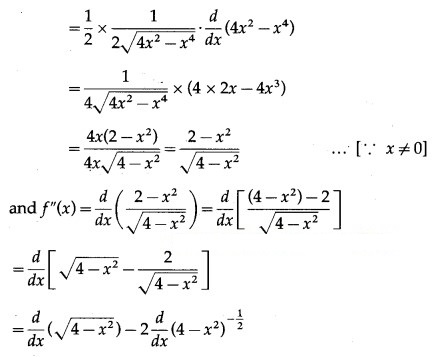
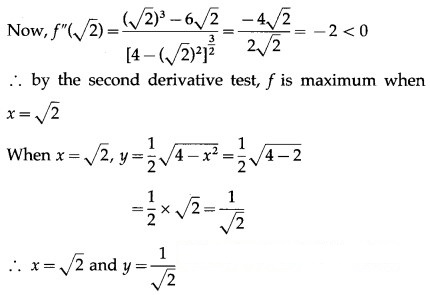
Question 15.
An open cylindrical tank whose base is a circle is to be constructed of metal sheet so as to contain a volume of π cu cm of water. Find the dimensions so that the quantity of the metal sheet required is minimum.
Solution:
Let x be the radius of the base, h be the height, V be the volume and S be the total surface area of the cylindrical tank.
Then V = π … (Given)
∴ πx2h = π
Now, S = 2πxh + π
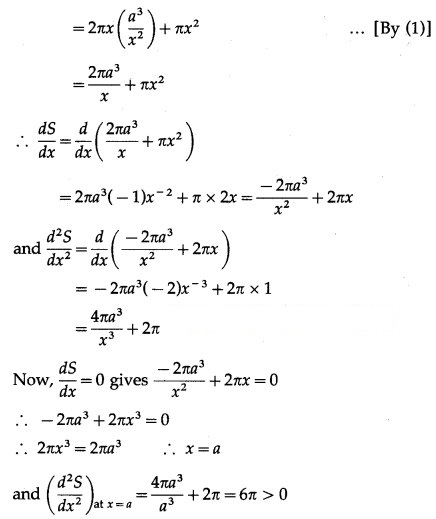
∴ by the second derivative test, S is minimum when x = a
When x = a, from (1)
Hence, the quantity of metal sheet is minimum when radius height = a cm.
Question 16.
The perimeter of a triangle is 10 cm. If one of the sides is 4 cm. What are the other two sides of the triangle for its maximum area?
Solution:
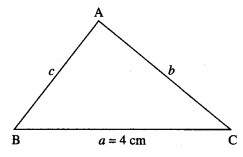
Let ABC be the triangle such that the side BC = a = 4 cm.
Also, the perimeter of the triangle is 10 cm.
i.e. a + b + c = 10
∴ 2s = 10
∴ s = 5
Also, 4 + b + c = 10
∴ b + c = 6
∴ b = 6 – c
Let ∆ be the area of the triangle.
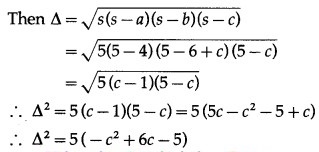
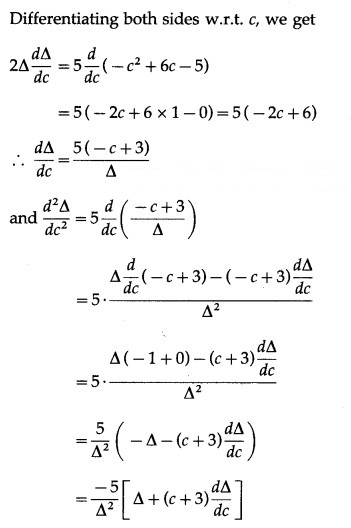
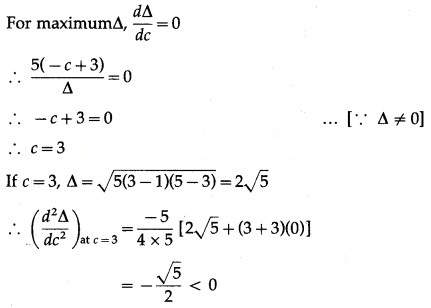
∴ by the second derivative test, ∆ is maximum when c = 3.
When c = 3, b = 6 – c = 6 – 3 = 3
Hence, the area of the triangle is maximum when the other two sides are 3 cm and 3 cm.
Question 17.
A box with a square base is to have an open top. The surface area of the box is 192 sq cm. What should be its dimensions in order that the volume is largest?
Solution:
Let x cm be the side of square base and h cm be its height.
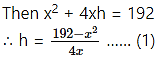
Let V be the volume of the box.
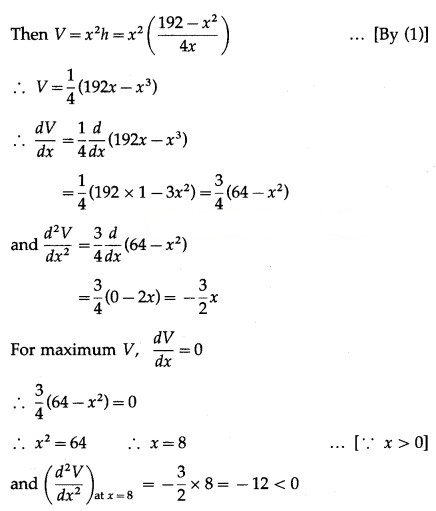
∴ by the second derivative test, V is maximum at x = 8.
Hence, the volume of the box is largest, when the side of square base is 8 cm and its height is 4 cm.
Question 18.
The profit function P (x) of a firm, selling x items per day is given by P(x) = (150 – x)x – 1625. Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit.
Solution:
Profit function P (x) is given by
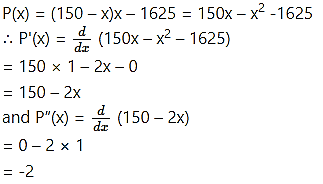
Now, P'(x) = 0 gives, 150 – 2x = 0
∴ x = 75
and P”(75) = -2 < 0
∴ by the second derivative test, P(x) is maximum when x = 75
Maximum profit = P(75)
= (150 – 75)75 – 1625
= 75 × 75 – 1625
= 4000
Hence, the profit will be maximum, if the manufacturer manufactures 75 items and the maximum profit is 4000.
Question 19.
Find two numbers whose sum is 15 and when the square of one multiplied by the cube of the other is maximum.
Solution:
Let the two numbers be x and y.
Then x + y = 15
∴ y = 15 – x
Let P is the product of square of y and cube of x.
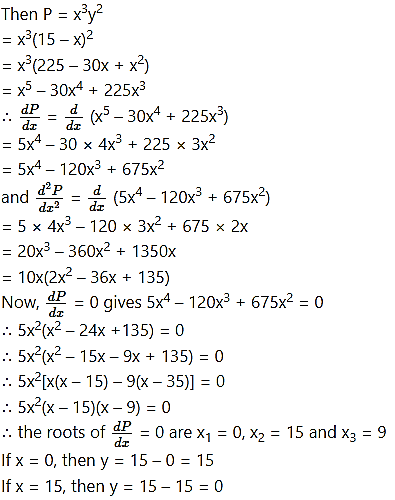
Question 20.
Show that among rectangles of given area, the square has least perimeter.
Solution:
Let x be the length and y be the breadth of the rectangle whose area is A sq units (which is given as constant).
Then xy = A
∴ y = A/x………(1)
Let P be the perimeter of the rectangle.
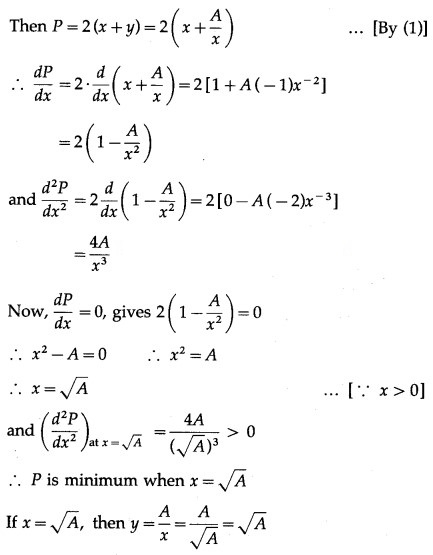
x = y
∴ rectangle is a square.
Hence, among rectangles of given area, the square has least perimeter.
Question 21.
Show that the height of a closed right circular cylinder of given volume and least surface area is equal to its diameter.
Solution:
Let x be the radius of base, h be the height and S be the surface area of the closed right circular cylinder whose volume is V which is given to be constant.
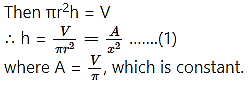
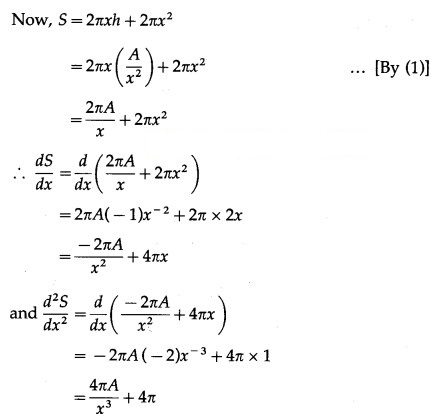
Hence, the surface area is least when height of the closed right circular cylinder is equal to its diameter.
Question 22.
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
Solution:
Let R be the radius and h be the height of the cylinder which is inscribed in a sphere of radius r cm.
Then from the figure,
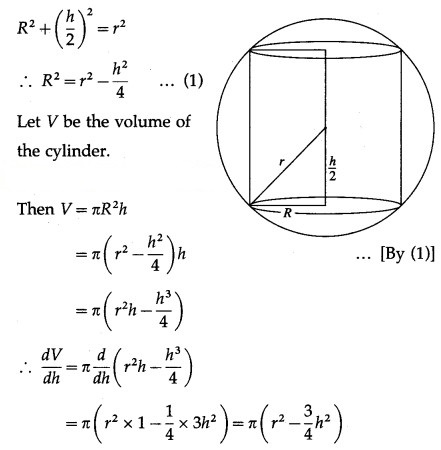
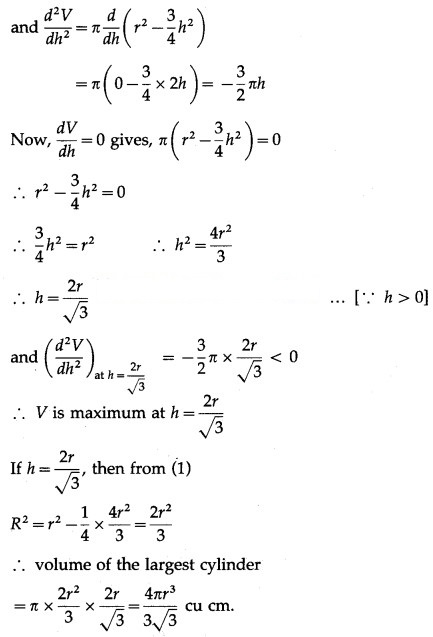
Question 23.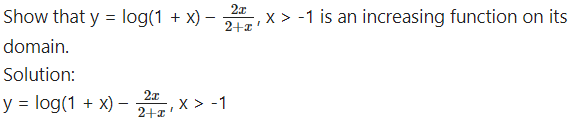
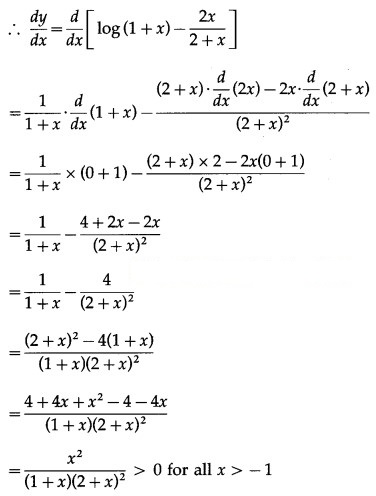
Hence, the given function is increasing function on its domain.
Question 24.
