Blog

Chapter 2 Trigonometry – I Ex 2.2

Chapter 2 Trigonometry – I Ex 2.2

Question 1.

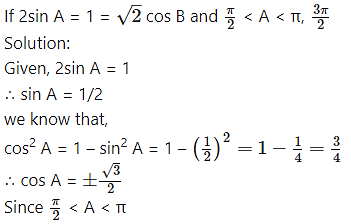
A lies in the 2nd quadrant.

We know that,

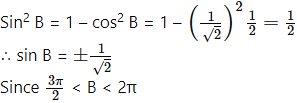
B lies in the 4th quadrant,

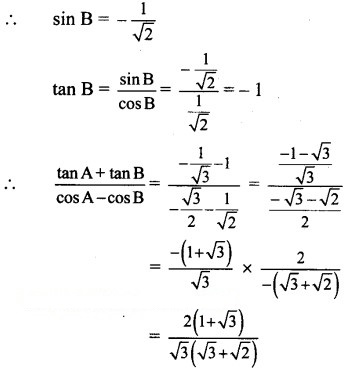
Question 2.
If and A, B are angles in the second quadran, then prove that 4cosA + 3 cos B = -5
Solution:

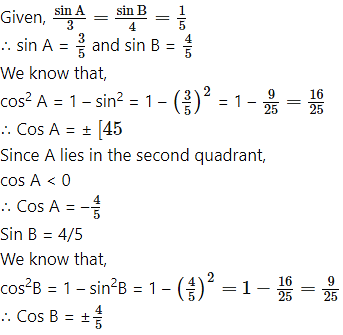
Since B lies in the second quadrant, cos B < 0

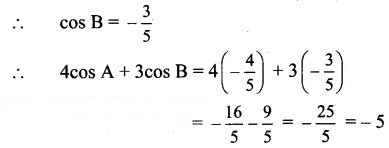
Question 3.

Solution:

Question 4.
Eliminate 0 from the following:
i. x = 3sec θ, y = 4tan θ
ii. x = 6cosec θ,y = 8cot θ
iii. x = 4cos θ – 5sin θ, y = 4sin θ + 5cos θ
iv. x = 5 + 6 cosec θ,y = 3 + 8 cot θ
v. x = 3 – 4tan θ,3y = 5 + 3sec θ
Solution:
i. x = 3sec θ, y = 4tan θ


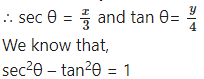
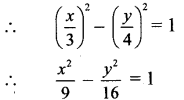
∴ 16x² – 9y² = 144

ii. x = 6cosec θ and y = 8cot θ
.’. cosec θ =  and cot θ = 
We know that,
cose θ – co θ =

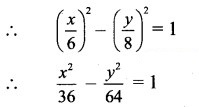
16 – 9 = 576

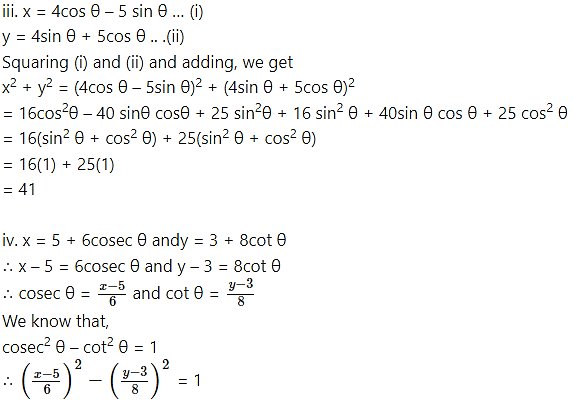
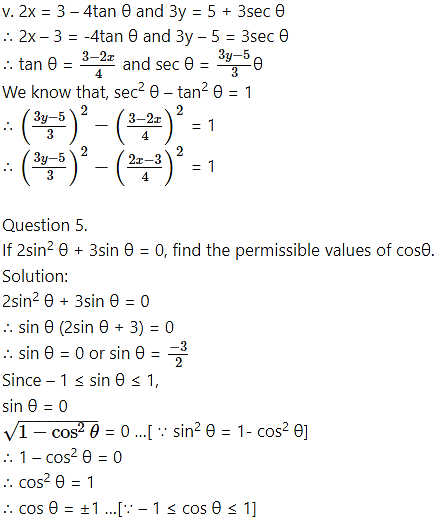
Question 7.

Question 8.
Find the acute angle 0 such that 5tan2 0 + 3 = 9sec 0.
Solution:

Question 9.
Find sin θ such that 3cos θ + 4sin θ = 4.
Solution:

Question 10.
If cosec θ + cot θ = 5, then evaluate sec θ.
Solution:

Question 11.

Solution:
We know that,

[Note: The question has been modified.]

Question 12.
Find the Cartesian co-ordinates of points whose polar co-ordinates are:
i. (3, 90°) ii. (1, 180°)
Solution:
i. (r, θ) = (3, 90°)
Using x = r cos θ and y = r sin θ, where (x, y) are the required cartesian co-ordinates, we get
x = 3cos 90° and y = 3sin 90°
∴ x = 3(0) = 0 and y = 3(1) = 3
∴ the required cartesian co-ordinates are (0, 3).

ii. (r, θ) = (1, 180°)
Using x = r cos θ and y = r sin θ, where (x, y) are the required cartesian co-ordinates, we get
x = 1(cos 180°) and y = 1(sin 180°)
∴ x = -1 and y = 0
∴ the required cartesian co-ordinates are (-1, 0).

Question 13.
Find the polar co-ordinates of points whose Cartesian co-ordinates are:

Question 14.

dhana work.txt
Displaying dhana work.txt.