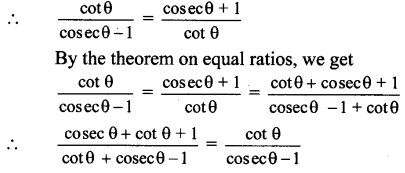Chapter 2 Trigonometry – I Miscellaneous Exercise 2
Chapter 2 Trigonometry – I Miscellaneous Exercise 2
I. Select the correct option from the given alternatives.
Question 1.
The value of the expression
cos1°. cos2°. cos3° … cos 179° =
(A) -1
(B) 0
(D) 1
Answer:
(B) 0
Explanation:
cos 1° cos 2° cos 3° … cos 179°
= cos 1° cos 2° cos 3° … cos 90°… cos 179°
= 0 …[∵ cos 90° = 0]
Question 2.
(A) 2cosec A
(B) 2 sec A
(C) 2 sin A
(D) 2 cos A
Answer:
(A) 2cosec A
Explanation:
Question 3.
Explanation:
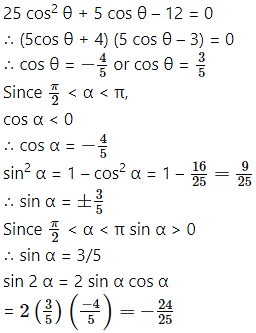
Question 4.
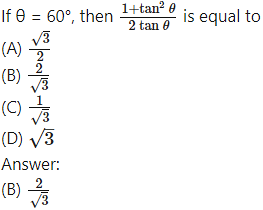
Explanation:
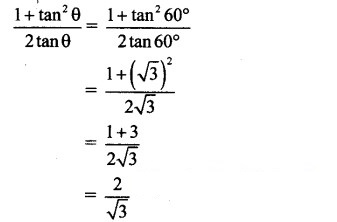
Question 5.
(A) 2
(B) mn
(C) 2m
(D) 2n
Answer:
(A) 2
Explanation:
Question 6.
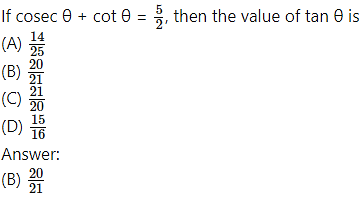
Explanation:
Question 7.
(A) 0
(B) 1
(C) sin θ
(D) cos θ
Answer:
(D) cos θ
Explanation:
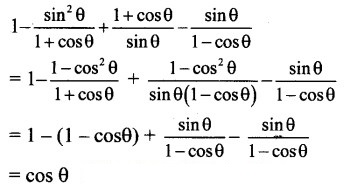
Question 8.
If cosec θ – cot θ = q, then the value of cot θ is
Question 9.
(A) A.P.
(B) G.P.
(C) H.P.
(D) Not in progression
Answer:
(B) G.P.
Explanation:
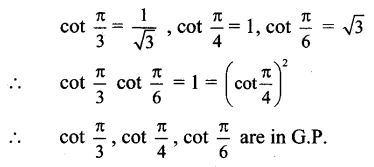
Question 10.
The value of tan 1°.tan 2° tan 3° equal to
(A) -1
(B) 1
(D) 2
Answer:
(B) 1
Explanation:
tan1° tan2° tan3° … tan89°
= (tan 1° tan 89°) (tan 2° tan 88°)
…(tan 44° tan 46°) tan 45°
= (tan 1 ° cot 1 °) (tan 2° cot 2°)
…(tan 44° cot 44°) . tan 45°
…tan(∵ 90° – θ) = cot θ]
= 1 x 1 x 1 x … x 1 x tan 45° =1
II. Answer the following:
Question 1.
Find the trigonometric functions of:
90°, 120°, 225°, 240°, 270°, 315°, -120°, -150°, -180°, -210°, -300°, -330°
Solution:
Angle of measure 90° :
Let m∠XOA = 90°
Its terminal arm (ray OA)
intersects the standard, unit circle at P(0, 1).
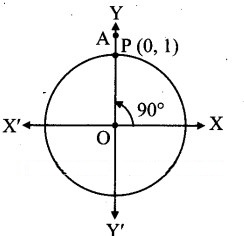
∴ x = 0 and y = 1
sin 90° = y = 1
cos 90° = x = 0
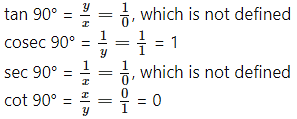
Angle of measure 120° :
Let m∠XOA =120°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1
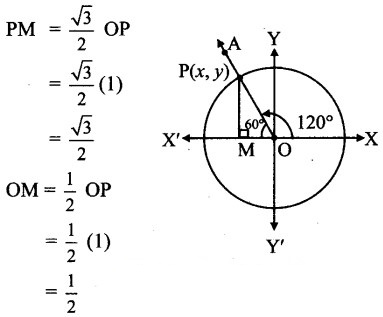
Since point P lies in the 2nd quadrant, x < 0, y > 0
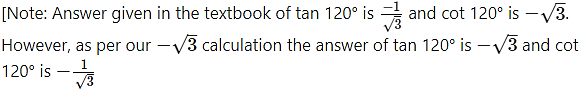
Angle of measure 225° :
Let m∠XOA = 225°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 45° – 45° – 90° triangle.
OP = 1
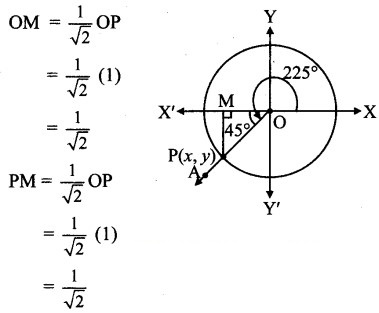
Since point P lies in the 3rd quadrant, x < 0, y < 0
Angle of measure 240° :
Let m∠XOA = 240°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 30° – 60° – 90° triangle.
OP = 1
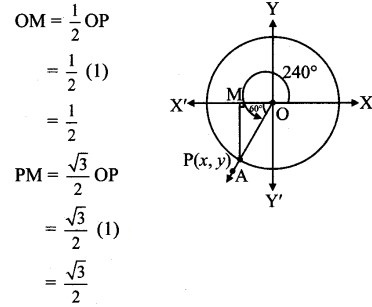
Since point P lies in the 3rd quadrant, x < 0, y < 0
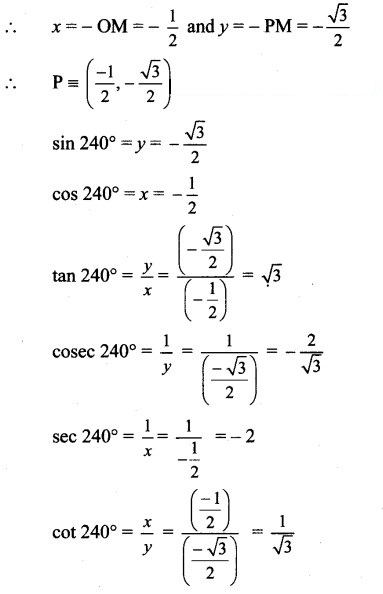
Angle of measure 270° :
Let m∠XOA = 270°
Its terminal arm (ray OA) intersects the standard unit circle at P(0, – 1).
x = 0 andy = – 1
sin 270° = y = -1
cos 270° = x = 0
tan 270° =
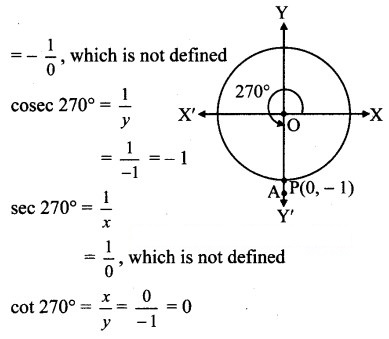
Angle of measure 315° :
Let m∠XOA = 315°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 45° – 45° – 90° triangle.
OP = 1
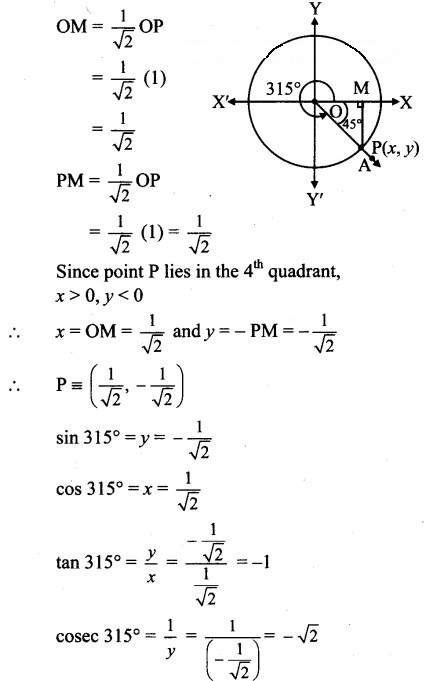
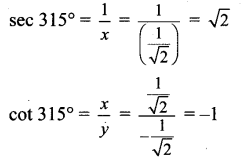
[Note: Answer given in the textbook of cot 315° is 1. However, as per our calculation it is -1.]
Angle of measure (-120°):
Let m∠XOA = – 120°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,
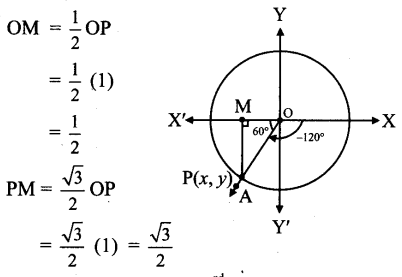
Since point P lies in the 3rd quadrant, x < 0, y < 0
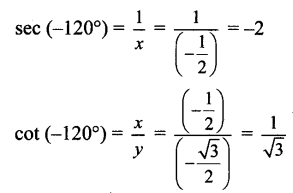
Angle of measure (-150°) :
Let m∠XOA = – 150°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1
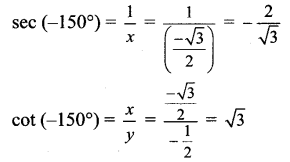
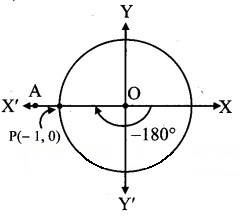
Angle of measure (-180°):
Let m∠XOA = – 180°
Its terminal arm (ray OA) intersects the standard unit circle at P(- 1, 0).
∴ x = – 1 andy = 0
sin (-180°) = y = 0
cos (-180°) = x
= -1
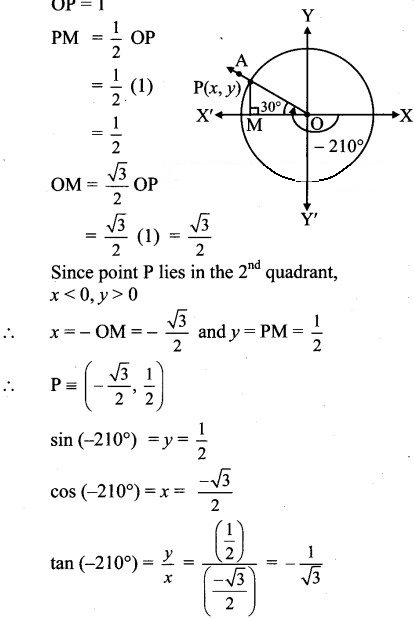
Angle of measure (- 210°):
Let m∠XOA = -210°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1
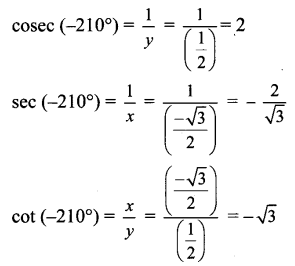
Angle of measure (- 300°):
Let m∠XOA = – 300° Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 30° – 60° – 90° triangle.
OP = 1
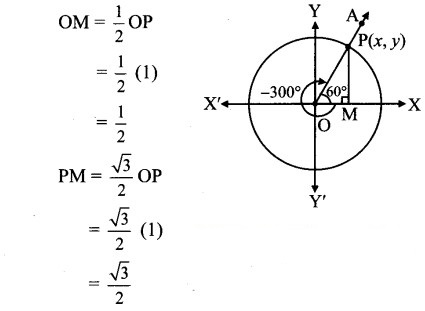
Since point P lies in the 1st quadrant, x>0,y>0
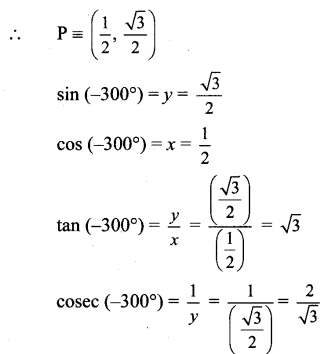
Angle of measure (- 330°):
Let m∠XOA = – 330°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1
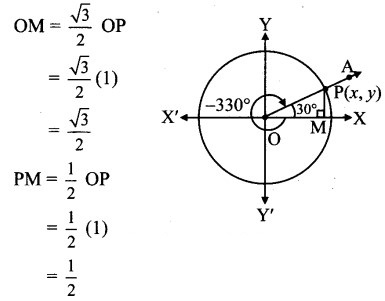
Since point P lies in the 1st quadrant, x > 0, y > 0
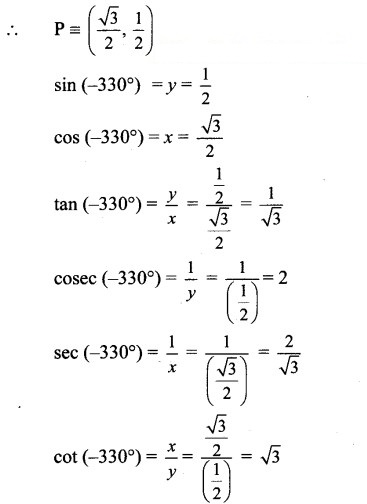
Question 2.
State the signs of:
i. cosec 520°
ii. cot 1899°
iii. sin 986°
Solution:
i. 520° =360° + 160°
∴ 520° and 160° are co-terminal angles.
Since 90° < 160° < 180°,
160° lies in the 2nd quadrant.
∴ 520° lies in the 2nd quadrant,
∴ cosec 520° is positive.
ii. 1899° = 5 x 360° + 99°
∴ 1899° and 99° are co-terminal angles.
Since 90° < 99° < 180°,
99° lies in the 2nd quadrant.
∴ 1899° lies in the 2nd quadrant.
∴ cot 1899° is negative.
iii. 986° = 2x 360° + 266°
∴ 986° and 266° are co-terminal angles.
Since 180° < 266° < 270°,
266° lies in the 3rd quadrant.
∴ 986° lies in the 3rd quadrant.
∴ sin 986° is negative.
Question 3.
State the quadrant in which 6 lies if
i. tan θ < 0 and sec θ > 0
ii. sin θ < 0 and cos θ < 0
iii. sin θ > 0 and tan θ < 0
Solution:
i. tan θ < 0 tan θ is negative in 2nd and 4th quadrants, sec θ > 0
sec θ is positive in 1st and 4th quadrants.
∴ θ lies in the 4th quadrant.
ii. sin θ < 0
sin θ is negative in 3rd and 4th quadrants, cos θ < 0
cos θ is negative in 2nd and 3rd quadrants.
.’. θ lies in the 3rd quadrant.
iii. sin θ > 0
sin θ is positive in 1st and 2nd quadrants, tan θ < 0
tan θ is negative in 2nd and 4th quadrants.
∴ θ lies in the 2nd quadrant.
Question 4.
Which is greater?
sin (1856°) or sin (2006°)
Solution:
1856° = 5 x 360° + 56°
∴ 1856° and 56° are co-terminal angles.
Since 0° < 56° < 90°, 56° lies in the 1st quadrant.
∴ 1856° lies in the 1st quadrant,
∴ sin 1856° >0 …(i)
2006° = 5 x 360° + 206°
∴ 2006° and 206° are co-terminal angles.
Since 180° < 206° < 270°,
206° lies in the 3rd quadrant.
∴ 2006° lies in the 3rd quadrant,
∴ sin 2006° <0 …(ii)
From (i) and (ii),
sin 1856° is greater.
Question 5.
Which of the following is positive?
sin(-310°) or sin(310°)
Solution:
Since 270° <310° <360°,
310° lies in the 4th quadrant.
∴ sin (310°) < 0
-310° = -360°+ 50°
∴ 50° and – 310° are co-terminal angles.
Since 0° < 50° < 90°, 50° lies in the 1st quadrant.
∴ – 310° lies in the 1st quadrant.
∴ sin (- 310°) > 0
∴ sin (- 310°) is positive.
Question 6.
Show that 1 – 2sin θ cos θ ≥ 0 for all θ ∈ R.
Solution:
1 – 2 sin θ cos θ
= si θ + co θ – 2sin θ cos θ
= (sin θ – cos θ ≥ 0 for all θ ∈ R
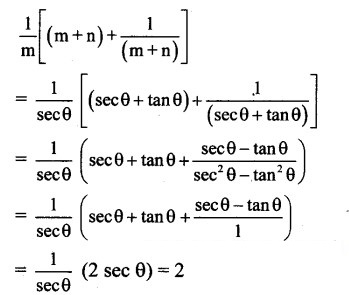
Question 7.
Show that ta θ + co θ ≥ 2 for all θ ∈ R.
Solution:
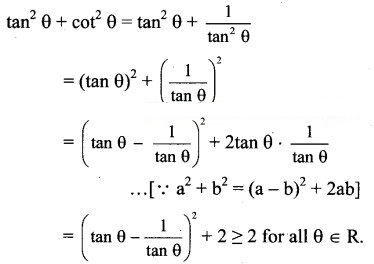
Question 8.
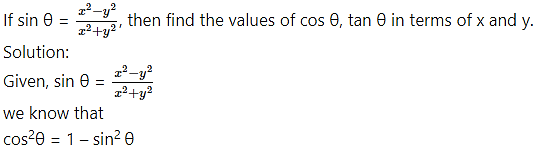
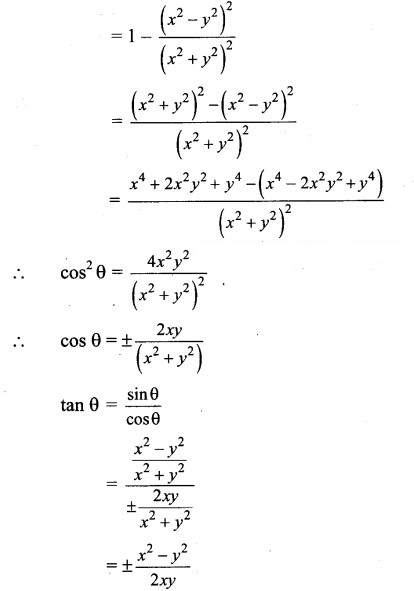
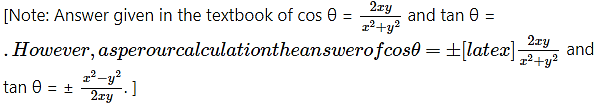
Question 9.
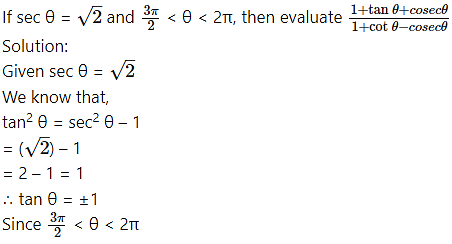
θ lies in the 4th quadrant.
∴ tan θ < 0
∴ tan θ = -1
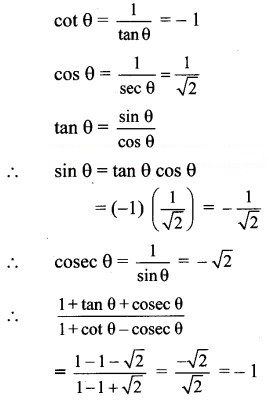
Question 10.
Prove the following:
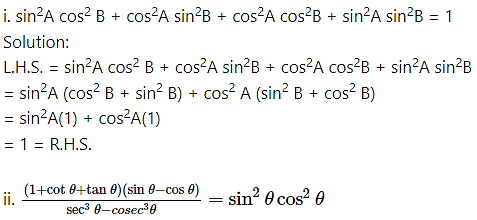
Solution:
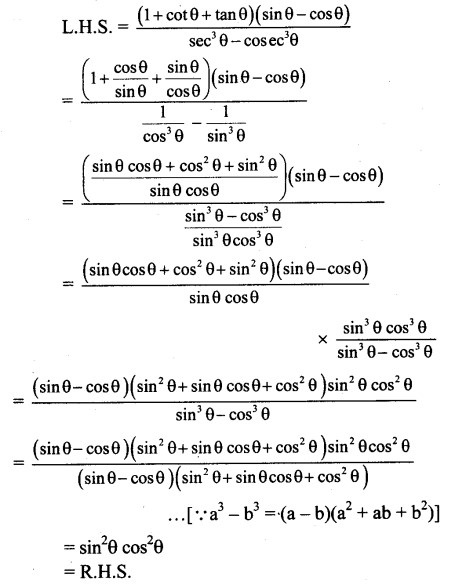
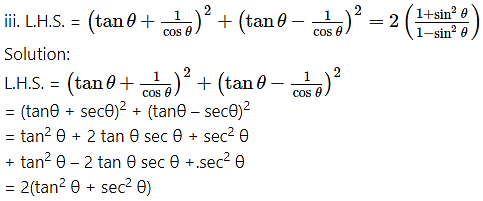
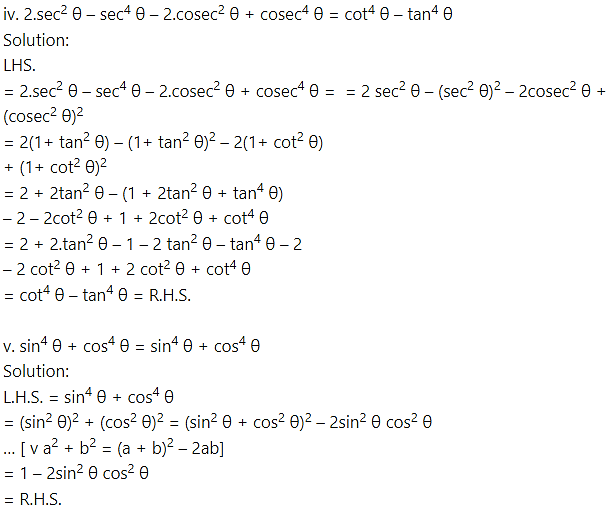
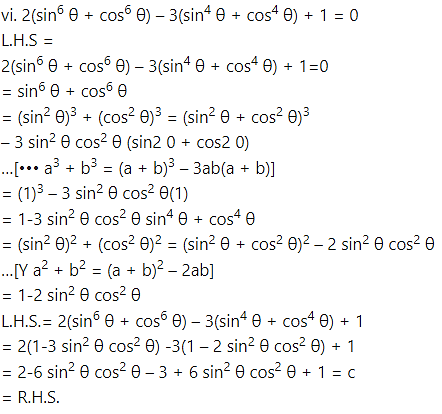
Solution:
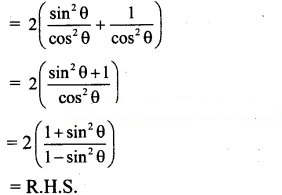
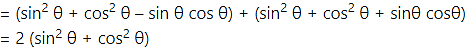
= 2(1)
= 2 = R.H.S.
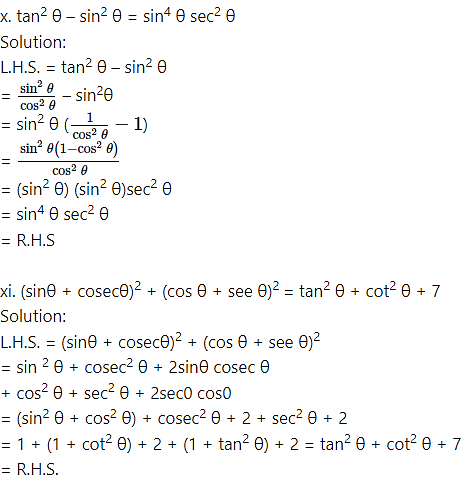
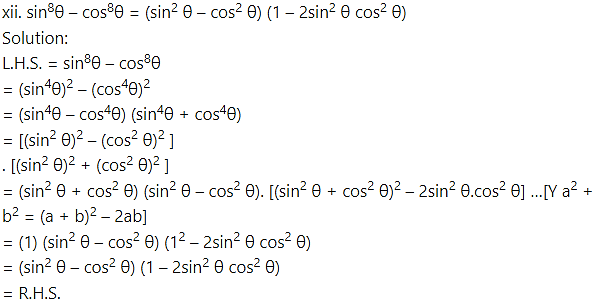
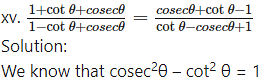
∴ (cosec θ – cot θ) (cosec θ + cot θ) = 1
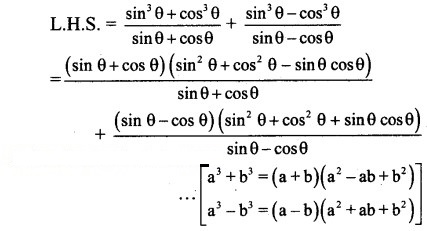
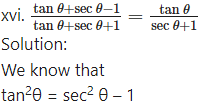
∴ tan θ. tanθ = (sec θ + 1)(sec θ – 1)
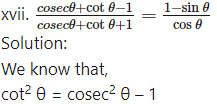
∴ cot θ . cot θ = (cosec θ + 1)(cosec θ – 1)
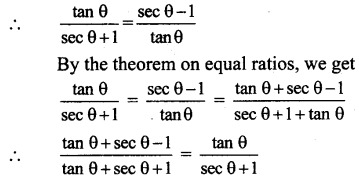
Alternate Method:
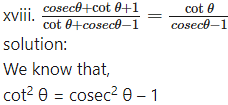
∴ cot θ.cot θ = (cosec θ + 1) (cosec θ – 1)
