Blog

Chapter 3 Trigonometry – II Miscellaneous Exercise 3

Chapter 3 Trigonometry – II Miscellaneous Exercise 3

I. Select the correct option from the given alternatives.

Question 1.
The value of sin(n + 1) A sin(n + 2) A + cos(n + 1) A cos(n + 2) A is equal to
(a) sin A
(b) cos A
(c) -cos A
(d) sin 2A
Answer:
(b) cos A
Hint:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let (n + 2)A = a and (n + 1)A = b … (i)
∴ L.H.S. = cos a . cos b + sin a . sin b
= cos (a – b)
= cos [(n + 2)A – (n + 1)A] ……..[From (i)]
= cos [(n + 2 – n – 1)A]
= cos A
= R.H.S.

Question 2.
If tan A – tan B = x and cot B – cot A = y, then cot (A – B) = ________

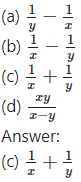
Hint:

Question 3.
If sin θ = n sin(θ + 2α), then tan(θ + α) is equal to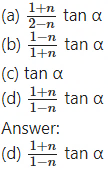

Hint:

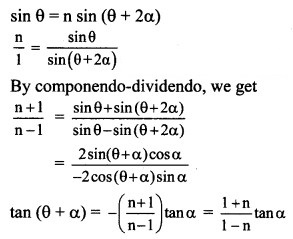
Question 4.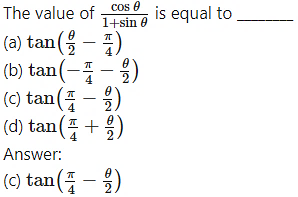

Hint:

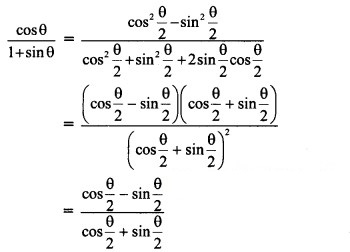
Question 5.
The value of cos A cos (60° – A) cos (60° + A) is equal to ________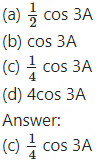

Hint:

Question 6.

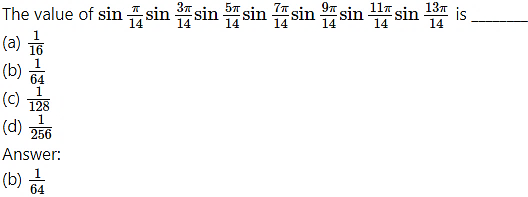
Hint:

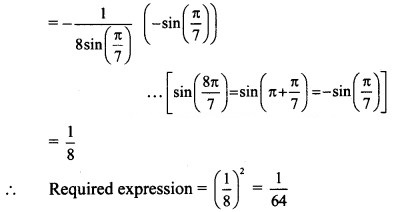
Question 7.

Question 8.

Question 9.
In ∆ABC if cot A cot B cot C > 0, then the triangle is ________
(a) acute-angled
(b) right-angled
(c) obtuse-angled
(d) isosceles right-angled
Answer:
(a) acute angled
Hint:
cot A cot B cot C > 0
Case I:
cot A, cot B, cot C > 0
∴ cot A > 0, cot B > 0, cot C > 0

∴ ∆ABC is an acute angled triangle.
Case II:
Two of cot A, cot B, cot C < 0
0 < A, B, C < π and two of cot A, cot B, cot C < 0
∴ Two angles A, B, C are in the 2nd quadrant which is not possible.

Question 10.
The numerical value of tan 20° tan 80° cot 50° is equal to ________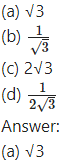

Hint:
L.H.S. = tan 20° tan 80° cot 50°
= tan 20° tan 80° cot (90° – 40°)
= tan 20° tan 80° tan 40°
= tan 20° tan (60° + 20°) tan (60° – 20°)

= tan 3(20°)
= tan 60°
= √3
= R.H.S.

II. Prove the following.

Question 1.
tan 20° tan 80° cot 50° = √3
Solution:
L.H.S. = tan 20° tan 80° cot 50°
= tan 20° tan 80° cot (90° – 40°)
= tan 20° tan 80° tan 40°
= tan 20° tan (60° + 20°) tan (60° – 20°)

= tan 3(20°)
= tan 60°
= √3
= R.H.S.

Question 2.
If sin α sin β – cos α cos β + 1 = 0, then prove that cot α tan β = -1.
Solution:
sin α sin β – cos α cos β + 1 = 0
∴ cos α cos β – sin α sin β = 1
∴ cos (α + β) = 1
∴ α + β = 0 ……[∵ cos 0 = 1]
∴ β = -α
L.H.S. = cot α tan β
= cot α tan(-α)
= -cot α tan α
= -1
= R.H.S.

Question 3.

Solution:

Question 4.

Solution:

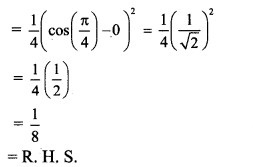
Question 5.

Solution:

Question 6.

Solution:

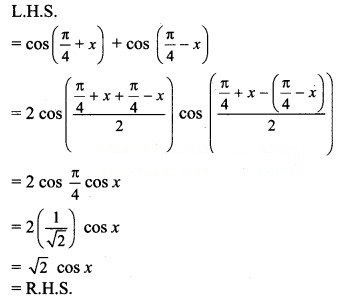
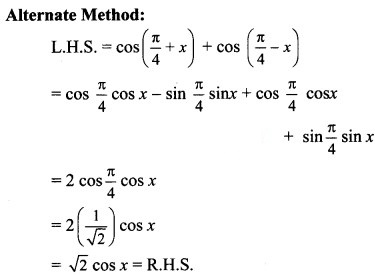
Question 7.

Solution:

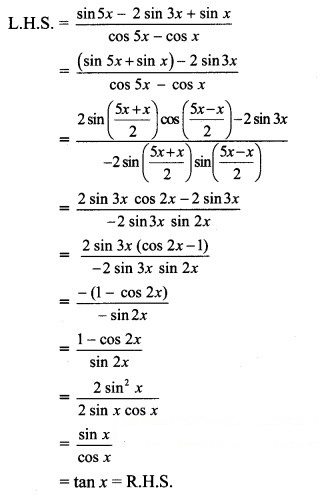
Question 8.
 6x –  4x = sin 2x sin 10x
Solution:

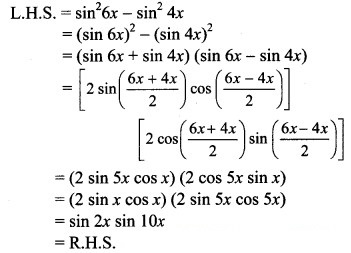
Question 9.
 2x –  6x = sin 4x sin 8x
Solution:

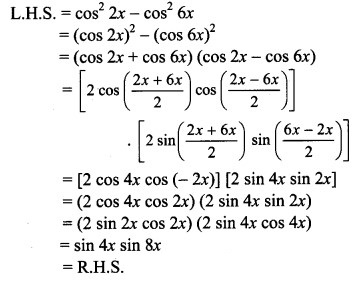
Question 10.
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Solution:

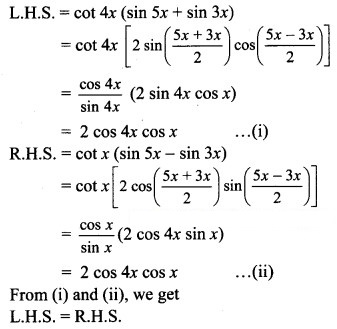
Question 11.

Solution:

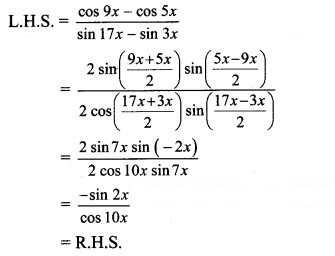
Question 12.

Solution:

Question 13.

Solution:

Question 14.
tan A + tan (60° + A) + tan (120° + A) = 3 tan 3A
Solution:

Question 15.
3  10° – 27 tan⁴ 10° + 33  10° = 1
Solution:

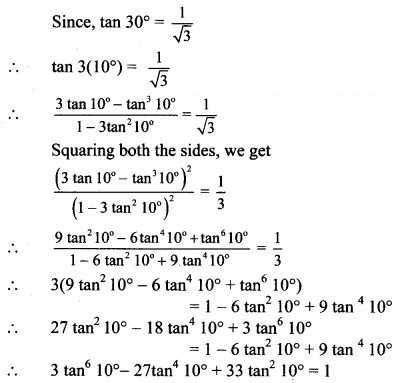
Question 16.
cosec 48° + cosec 96° + cosec 192° + cosec 384° = 0
Solution:
L.H.S. = cosec 48° + cosec 96° + cosec 192° + cosec 384°
= cosec 48° + cosec (180° – 84°) + cosec (180° + 12°) + cosec (360° + 24°)
= cosec 48° + cosec 84° + cosec (-12°) + cosec 24°

Question 17.

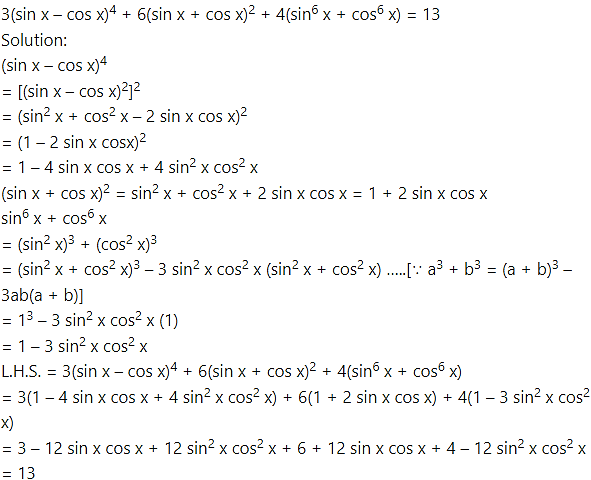
= R.H.S.

Question 18.
tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A = cot A
Solution:
We have to prove that,
tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A = cot A
i.e., to prove,
cot A – tan A – 2 tan 2A – 4 tan 4A – 8 cot 8A = 0

∴ cot θ – tan θ = 2 cot 2θ …..(i)
L.H.S. = cot A – tan A – 2 tan 2A – 4 tan 4A – 8 cot 8A
= 2 cot 2A – 2 tan 2A – 4 tan 4A – 8 cot 8A …..[From (i)]
= 2(cot 2A – tan 2A) – 4 tan 4A – 8 cot 8A
= 2 × 2 cot 2(2A) – 4 tan 4A – 8 cot 8A ……[From (i)]
= 4(cot 4A – tan 4A) – 8 cot 8A
= 4 × 2 cot 2(4A) – 8 cot 8A ……[From (i)]
= 8 cot 8A – 8 cot 8A = 0
= R.H.S.
Alternate Method:

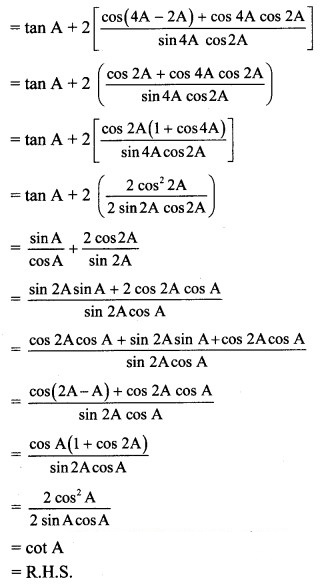
Question 19.

Solution:

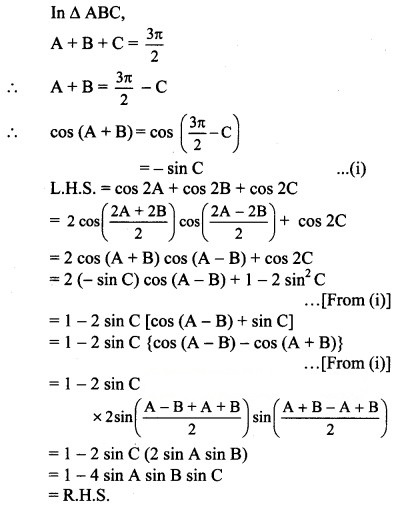
Question 20.

Solution:
sin A – cos B = cos C
∴ sin A = cos B + cos C

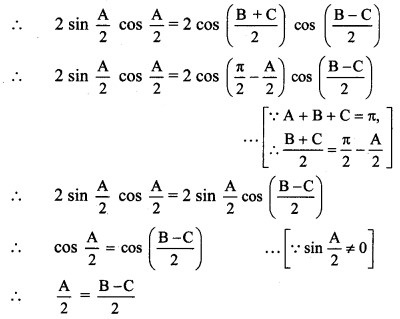
A = B – C ………(i)
In ∆ABC,
A + B + C = π
∴ B – C + B + C = π
∴ 2B = π
∴ B = 

Question 21.

Solution:

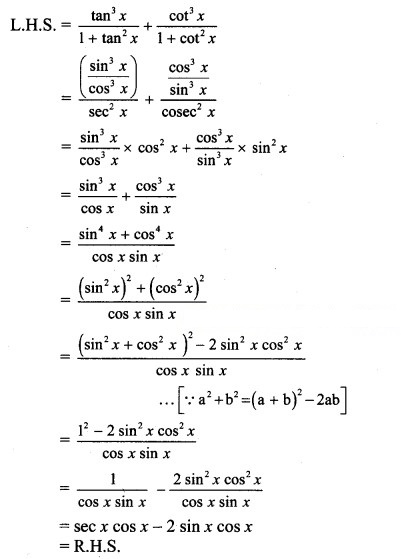
Question 22.

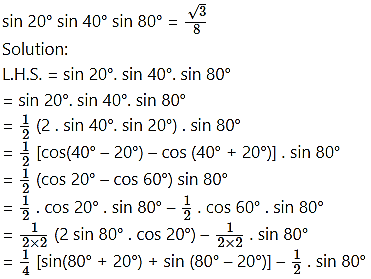
Question 23.

Solution:
Let θ = 18°
∴ 5θ = 90°
∴ 2θ + 3θ = 90°
∴ 2θ = 90° – 3θ
∴ sin 2θ = sin (90° – 3θ)
∴ sin 2θ = cos 3θ
∴ 2 sin θ cos θ = 4 cos³ θ – 3 cos θ
∴ 2 sin θ = 4 cos² θ – 3 …..[∵ cos θ ≠ 0]
∴ 2 sin θ = 4 (1 – sin² θ) – 3
∴ 2 sin θ = 1 – 4 sin² θ
∴ 4 sin² θ + 2 sin θ – 1 = 0

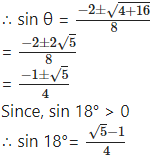
Question 24.

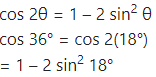
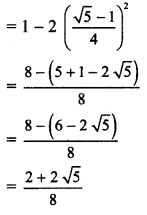
Question 25.

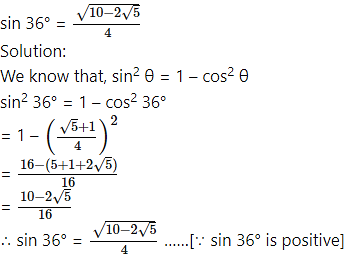
Question 26.

Solution:

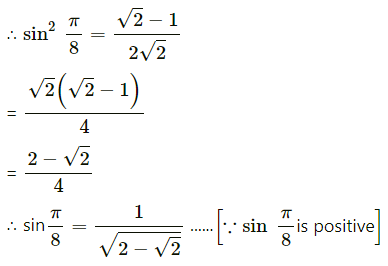
Question 27.

Solution:

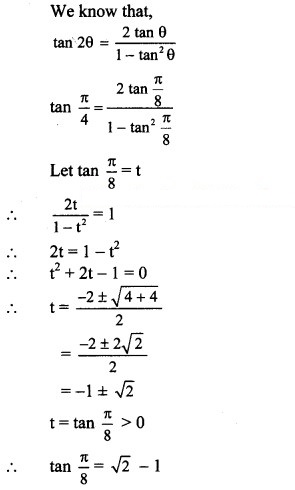
Question 28.
tan 6° tan 42° tan 66° tan 78° = 1
Solution:

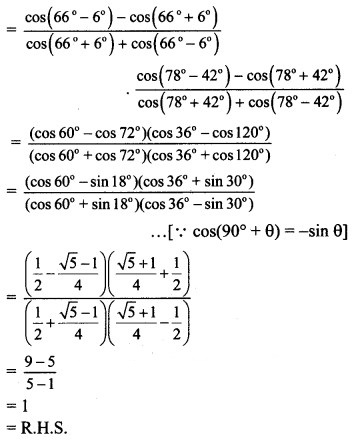
Question 29.
sin 47° + sin 61° – sin 11° – sin 25° = cos 7°
Solution:

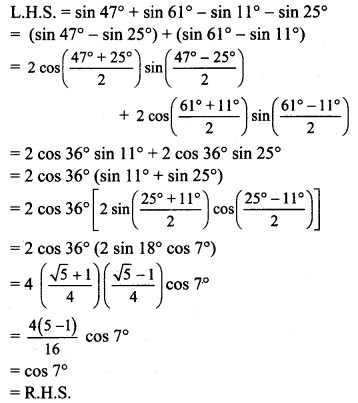
Question 30.
√3 cosec 20° – sec 20° = 4
Solution:

Question 31.

Solution: