Blog

Chapter 4 Angles and Pairs of Angles Set 4.5

Question 1.
Draw the pairs of angles as described below. If that is not possible, say why.
i. Complementary angles that are not adjacent.
ii. Angles in a linear pair which are not supplementary.
iii. Complementary angles that do not form a linear pair.
iv. Adjacent angles which are not in linear pair.
v. Angles which are neither complementary nor adjacent.
vi. Angles in a linear pair which are complementary.
Solution:
i.

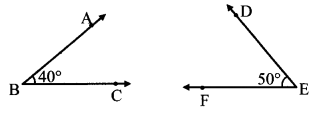
ii. Sum of angles in a linear pair is 180°.
i.e. they are supplementary .
∴ Angles in a linear pair which are not supplementary cannot be drawn.

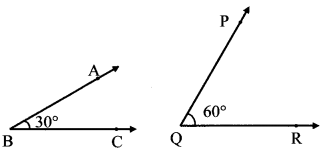
iii.

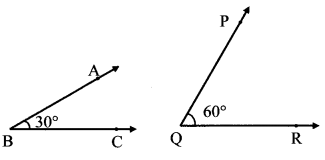
iv.

v.

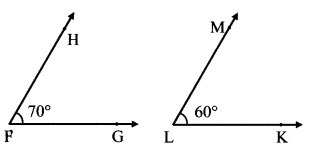
vi. Angles in linear pair have their sum as 180° But, complementary angles have their sum as 90°.
∴ Angles in a linear pair which are complementary cannot be drawn.

Note: Problem No. i, iii, iv, and v have more than one answers students may draw angles other than the once given.

Intext Questions and Activities

Question 1.
Observe the adjacent figure and answer the following questions: (Textbook pg. no. 29)

1. Write the names of the angles in the figure alongside.
2. What type of a pair of angles is it?
3. Which arms of the angles are not the common arms?
4. m∠PQR = __.
5. m∠RQS = __.

Solution:

1. ∠PQR and ∠RQS
2. Angles in a linear pair
3. Ray QP and ray QS
4. 125
5. 55
   Here, m∠PQR + m∠RQS = 125° + 55°
   = 180°
   ∴The adjacent angles ∠PQR and ∠RQS are supplementary.