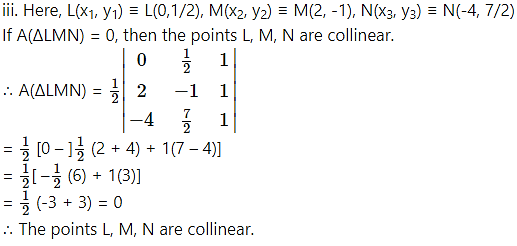Chapter 4 Determinants and Matrices Ex 4.3
Chapter 4 Determinants and Matrices Ex 4.3
Question 1.
Solve the following linear equations by using Cramer’s Rule.
x+y + z = 6, x – y + z = 2,.x + 2y – z = 2
x + y – 2z = -10,
2x +y – 3z = -19, 4x + 6y + z = 2
= 6(1 – 2) – 1(-2 – 2) + 1(4 + 2)
= 6(-1) -1 (-4) + 1(6)
= -6 + 4 + 6
= 4
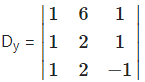
= 1(-2 – 2) – 6(-l – 1) + 1(2 = 1 (- 4) – 6 (- 2) + 1(0)
= -4+12 + 0 = 8
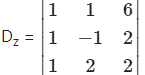
= l(-2 – 4) – 1(2 – 2) + 6(2 + 1)
= l(-6)-l(0) + 6(3)
= -6 + 0+18 = 12
By Cramer’s Rule,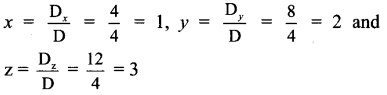 
∴ x = 1, y = 2 and z = 3 are the solutions of the given equations.
ii. Given equations are x+y- 2z = -10,
2x + y – 3z = -19,
Ax + 6y + z = 2. 
= 1(1 + 18)- 1(2+ 12)-2(12-4)
= 1(19)-1(14)-2(8)
= 19-14-16 = -11 ≠ 0
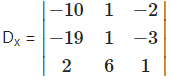
= -10(1 + 18) – 1(-19 + 6) – 2(- 114 – 2)
= -10(19)- 1(-13) -2(-l 16)
= -190+ 13 + 232 = 55
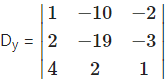
= 1(-19 + 6) – (-10)(2 + 12) – 2(4 + 76) = 1(-13) + 10(14) – 2(80)
= -13 + 140-160 = -33
= 1(2+ 114)-1(4+ 76)-10(12-4)
= 1(116)-1(80)-10(8)
= 116-80-80 .
= -44
By Cramer’s Rule,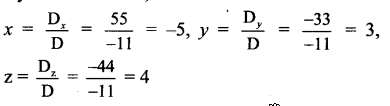 
∴ x = -5, y = 3 and z = 4 are the solutions of the given equations.
[Note: The question has been modified]
iii. Given equations are
x + z = 1, i.e.,x + 0y + z = 1,
y + z = 1, i.e., 0x + y + z = 1,
x + y = 4, i.e., x + y + 0z = 4. 
= 1(0 – 1) – 0 + 1(0 – 1)
= 1(-1)+1(-1)
= -1-1 = -2 ≠ 0
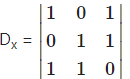
= 1(0 – 1) – 0 + 1(1 -4) = l(-l)+l(-3)
= -1 – 3
= -4
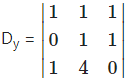
= 1(0 – 4) – 1(0 – 1) + 1(0 – 1)
= 1(-4) – 1(-1) + 1(-1)
= -4 + 1 – 1
= -4
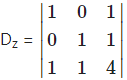
= 1(4 – 1) – 0 + 1(0 – 1)
= 1(3) + 1(-1)
= 3 – 1
= 2
By Cramer’s Rule, 
∴ x = 2, y = 2 and z = -1 are the solutions of the given equations.
∴ The given equations become
-2p – q – 3r = 3, i.e., 2p + q + 3r = -3,
2p-3q + r = -13,
2p – 3r = -11, i.e., 2p + 0q – 3r = -11.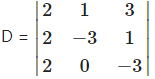 
= 2(9 – 0) – 1(-6 – 2) + 3(0 + 6)
= 2(9) – 1(-8) + 3(6)
= 18 + 8 + 18
= 44 ≠ 0
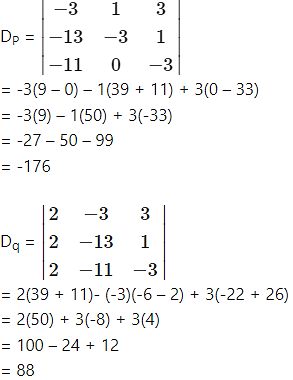
= 2(33 – 0) – 1(-22 + 26) – 3(0 + 6)
= 2(33) – 1(4) – 3(6)
= 66 – 4 – 18
= 44
By Cramer’s Rule,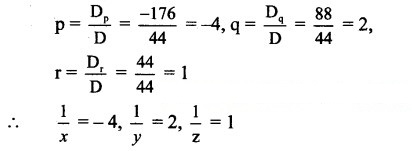 
Question 2.
The sum of three numbers is 15. If the second number is subtracted from the sum of first and third numbers, then we get 5. When the third number is subtracted from the sum of twice the first number and the second number, we get 4. Find the three numbers.
Solution:
Let the three numbers be x, y and z.
According to the given conditions, x + y + z = 15,
x + z-y = 5, i.e., x – y + z = 5,
2x + y – z = 4.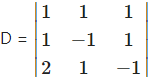 
= 1(1 – 1) – 1(-1 – 2) + 1(1 + 2)
= 1(0) – 1(-3) + 1(3)
= 0 + 3 + 3
= 6 ≠ 0
= 15(1 – 1) – 1(-5 – 4) + 1(5 + 4)
= 15(0) – 1(-9) + 1(9)
= 0 + 9 + 9
= 18
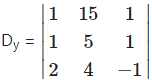
= 1(-5 – 4) – 15(-1 – 2) + 1(4 – 10)
= 1(-9) – 15(-3) + 1(-6)
= -9 + 45 – 6 = 30
= 1(-4 – 5) – 1(4 – 10) + 15(1 + 2)
= 1(-9) – 1(-6) + 15(3)
= -9 + 6 + 45
= 42
By Cramer’s Rule,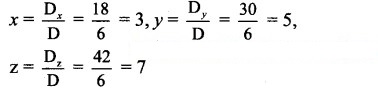 
∴ The three numbers are 3, 5 and 7.
Question 3.
Examine the consistency of the following equations.
i. 2x – y + 3 = 0, 3x + y – 2 = 0, 11x + 2y – 3 = 0
ii. 2x + 3y – 4 = 0, x + 2y = 3, 3x + 4y + 5 = 0
iii. x + 2y – 3 = 0,7x + 4y – 11 = 0,2x + 4y – 6 = 0
Solution:
i. Given equations are 2x – y + 3 = 0,
3x + y – 2 = 0,
11x + 2y – 3 = 0.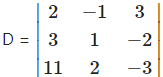 
= 2(-3 + 4) – (-l)(-9 + 22) + 3(6-11)
= 2(1)+1(13)+ 3(-5)
= 2 + 13-15 = 0
∴ The given equations are consistent.
ii. Given equations are 2x + 3y – 4 = 0,
x + 2y = 3, i.e., x + 2y – 3 = 0,
3x + 4y + 5 = 0. 
= 2(10 + 12) – 3(5 + 9) – 4(4 – 6)
= 2 (22) – 3(14) – 4(-2)
= 44 – 42 + 8
= 10 ≠ 0
∴ The given equations are not consistent.
iii. Given equations are x + 2y – 3 =
7x + 4y – 11 =0,
2x + 4y – 6 = 0.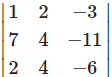 
= 1(-24 + 44) – 2(-42 + 22) – 3(28 – 8)
= 1(20) – 2(-20) – 3(20)
= 20 + 40 – 60
= 0
∴ The given equations are consistent.
Question 4.
Find k, if the following equations are consistent.
i. 2x + 3y-2 = 0,2x + 4y-k = 0,x-2j + 3k = 0
ii. kx + 3,y +1 = 0, x + 2y+1 = 0, x + y = 0
Solution:
i. Given equations are 2x + 3y – 2 = 0,
2x + 4y – k = 0,
x – 2y + 3k = 0.
Since these equations are consistent,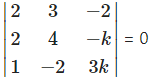 
∴ 2(12k – 2k) – 3(6k + k) – 2(- 4 – 4) = 0
∴ 2(10k) – 3(7k) – 2(- 8) = 0
∴ 20k – 21k + 16 = 0
∴ k = 16
Given equations are are
kx + 3y + 1 = 0,
x + 2y +1=0,
x + y = 0, i.e., x + y + 0 = 0.
Since these equations are consistent,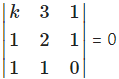 
∴ k(0 – 1) – 3(0 – 1) + 1(1 – 2) = 0
∴ k(-1) – 3(-1) + 1(-1) = 0
∴ -k + 3 – 1 = 0
∴ k = 2.
Question 5.
Find the area of triangle whose vertices are
i. A (5,8), B (5,0), C (1,0)
ii. P(3/2, 1), Q(4,2), R(4, -1/2)
iii. M (0, 5), N (- 2, 3), T (1, – 4)
Solution: 
Since area cannot be negative,
A(ΔABC) = 16 sq. units
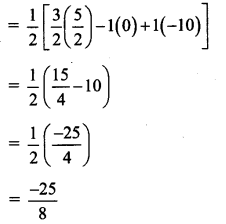
Since area cannot be negative
A(ΔPQR) = 25/8 sq. units
Question 6.
Find the area of quadrilateral whose vertices are A (- 3,1), B (- 2, – 2), C (1,4), D (3, – 1).
Solution:
A(-3, 1), B(-2, -2), C(l, 4), D(3, -1)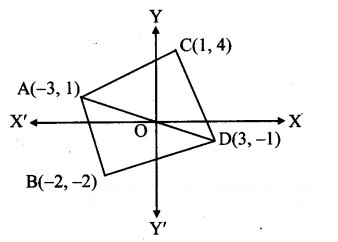 
∴ A(ΔADC) = 13 sq. units
∴ A(□ ABDC) = A(ΔABD) + A(ΔADC)
= 8 + 13
= 21 sq. units
Question 7.
Question 8.
Examine the collinearity of the following set of points:
i. A (3, – 1), B (0, – 3), C (12, 5)
ii. P (3, – 5), Q (6,1), R (4, 2)
iii. L(0,1/2), M(2,-1), N(-4, 7/2)
Solution: 
