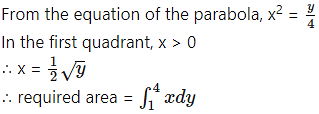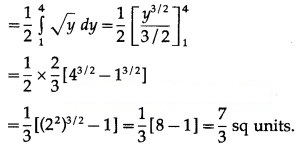Blog

Chapter 5 Application of Definite Integration Miscellaneous Exercise 5

Chapter 5 Application of Definite Integration Miscellaneous Exercise 5

I. Choose the correct option from the given alternatives:

Question 1.
The area bounded by the region 1 ≤ x ≤ 5 and 2 ≤ y ≤ 5 is given by
(a) 12 sq units
(b) 8 sq units
(c) 25 sq units
(d) 32 sq units
Answer:
(a) 12 sq units

Question 2.

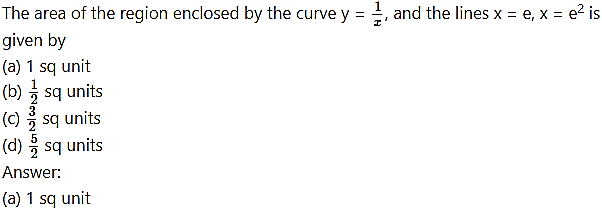
Question 3.

Question 5.

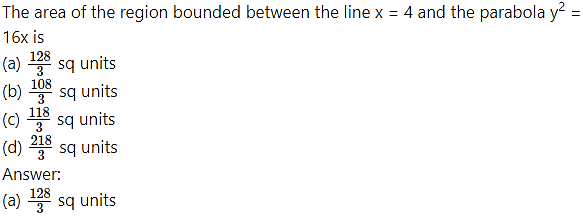
Question 6.
The area of the region bounded by y = cos x, Y-axis and the lines x = 0, x = 2π is
(a) 1 sq unit
(b) 2 sq units
(c) 3 sq units
(d) 4 sq units
Answer:
(d) 4 sq units

Question 7.

Question 9.

Question 11.

Question 13.

Question 15.

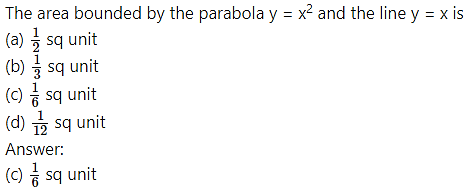
Question 16.

Question 18.

Question 20.

(II) Solve the following:

Question 1.
Find the area of the region bounded by the following curve, the X-axis and the given lines:
(i) 0 ≤ x ≤ 5, 0 ≤ y ≤ 2
(ii) y = sin x, x = 0, x = π
(iii) y = sin x, x = 0, x = π3
Solution:

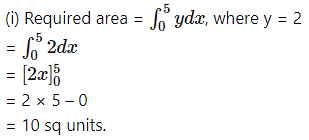
(ii) The curve y = sin x intersects the X-axis at x = 0 and x = π between x = 0 and x = π.

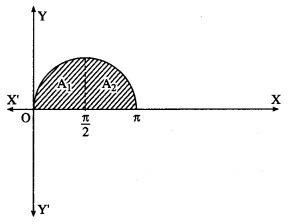
Two bounded regions  and  are obtained. Both the regions have equal areas.
∴ required area =

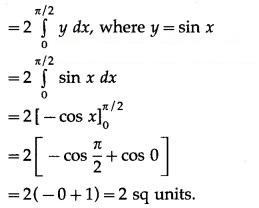
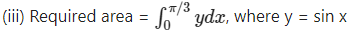
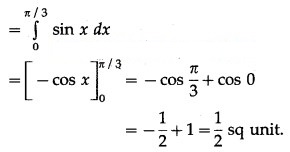
Question 2.
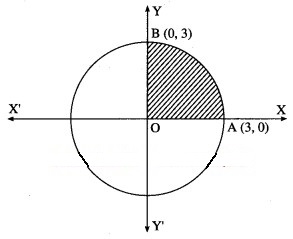
Find the area of the circle  = 9, using integration.
Solution:
By the symmetry of the circle, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 3.


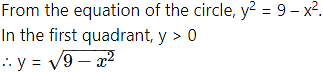
∴ area of the circle = 4 (area of the region OABO)

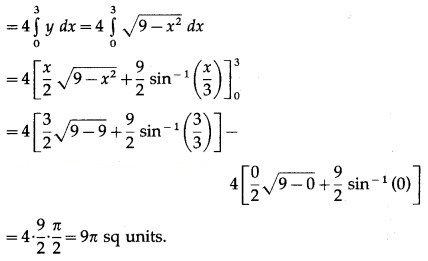
Question 3.

Solution:

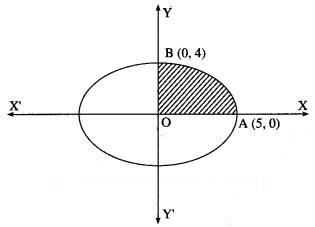
By the symmetry of the ellipse, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 5.
From the equation of the ellipse

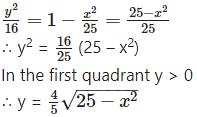
∴ area of the ellipse = 4(area of the region OABO)

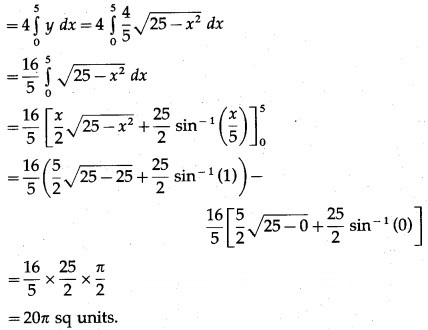
Question 4.
Find the area of the region lying between the parabolas: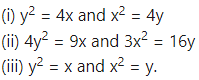

Solution:
(i)

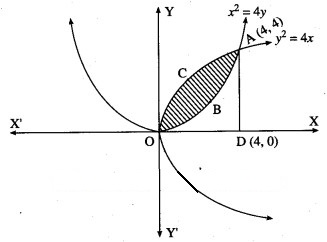
For finding the points of intersection of the two parabolas, we equate the values of  from their equations.

(ii)

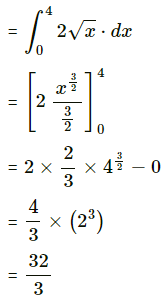
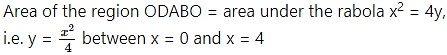
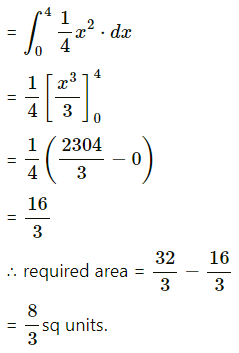
(iii)

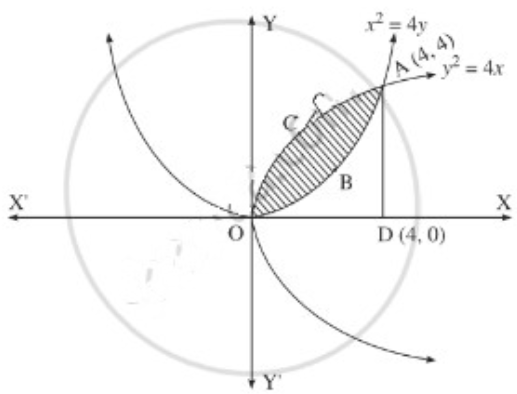
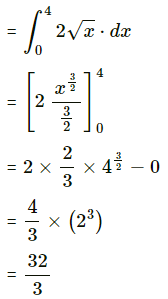
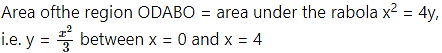
Question 5.
Find the area of the region in the first quadrant bounded by the circle  = 4 and the X-axis and the line x = y√3.
Solution:

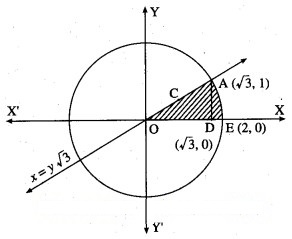
Question 6.
Find the area of the region bounded by the parabola  = x and the line y = x in the first quadrant.
Solution:
To obtain the points of intersection of the line and the parabola, we equate the values of x from both equations.

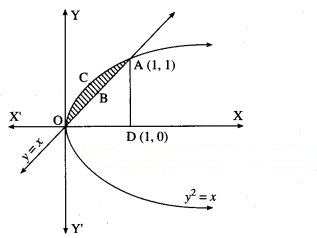
∴  = y
∴ – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = 0
When y = 1, x = 1
∴ the points of intersection are O(0, 0) and A(1, 1).
Required area = area of the region OCABO = area of the region OCADO – area of the region OBADO
Now, area of the region OCADO = area under the parabola  = x i.e. y = +√x (in the first quadrant) between x = 0 and x = 1

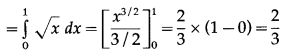
Area of the region OBADO = area under the line y = x between x = 0 and x = 1

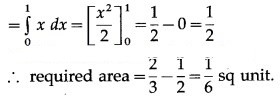
Question 7.
Find the area enclosed between the circle +  = 1 and the line x + y = 1, lying in the first quadrant.
Solution:

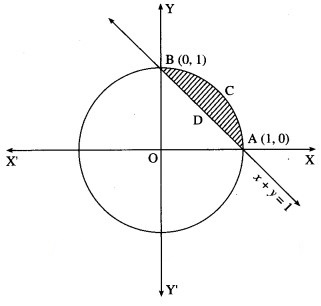
Required area = area of the region ACBPA = (area of the region OACBO) – (area of the region OADBO)
Now, area of the region OACBO = area under the circle +  =1 between x = 0 and x = 1

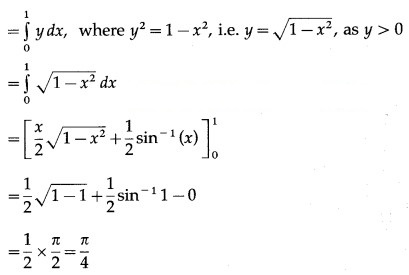
Area of the region OADBO = area under the line x + y = 1 between x = 0 and x = 1

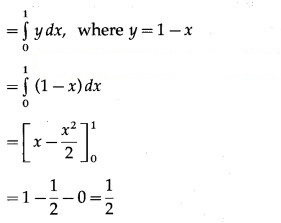
Question 8.
Find the area of the region bounded by the curve (y – 1 = 4(x + 1) and the line y = (x – 1).
Solution:
The equation of the curve is (y – 1 = 4(x + 1)
This is a parabola with vertex at A (-1, 1).
To find the points of intersection of the line y = x – 1 and the parabola.
Put y = x – 1 in the equation of the parabola, we get

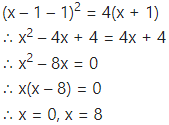
When x = 0, y = 0 – 1 = -1
When x = 8, y = 8 – 1 = 7
∴ the points of intersection are B (0, -1) and C (8, 7).

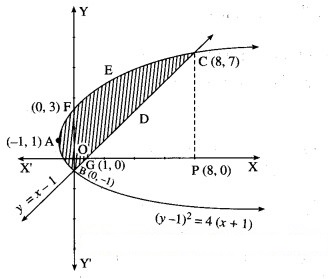
To find the points where the parabola (y – 1 = 4(x + 1) cuts the Y-axis.
Put x = 0 in the equation of the parabola, we get
(y – 1 = 4(0 + 1) = 4
∴ y – 1 = ±2
∴ y – 1 = 2 or y – 1 = -2
∴ y = 3 or y = -1
∴ the parabola cuts the Y-axis at the points B(0, -1) and F(0, 3).
To find the point where the line y = x – 1 cuts the X-axis.
Put y = 0 in the equation of the line, we get
x – 1 = 0
∴ x = 1
∴ the line cuts the X-axis at the point G (1, 0).
Required area = area of the region BFAB + area of the region OGDCEFO + area of the region OBGO
Now, area of the region BFAB = area under the parabola (y – 1 = 4(x + 1), Y-axis from y = -1 to y = 3

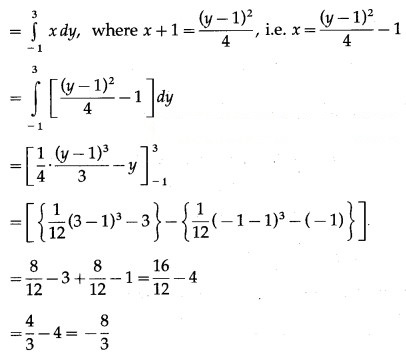
Since, the area cannot be negative,

Area of the region OGDCEFO = area of the region OPCEFO – area of the region GPCDG

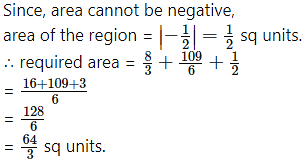
Question 9.
Find the area of the region bounded by the straight line 2y = 5x + 7, X-axis and x = 2, x = 5.
Solution:
The equation of the line is

Question 10.
Find the area of the region bounded by the curve y = 4, Y-axis and the lines y = 1, y = 4.
Solution:

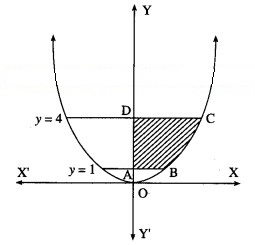
By symmetry of the parabola, the required area is 2 times the area of the region ABCD.