Chapter 5 Quadrilaterals Practice Set 5.2
Chapter 5 Quadrilaterals Practice Set 5.2
Question 1.
In the adjoining figure, □ABCD is a parallelogram, P and Q are midpoints of sides AB and DC respectively, then prove □APCQ is a parallelogram.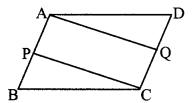
Given: □ABCD is a parallelogram. P and Q are the midpoints of sides AB and DC respectively.
To prove: □APCQ is a parallelogram.
Solution:

∴ AP = QC ….(iii) [From (i) and (ii)]
Also, AB || DC [Opposite angles of a parallelogram]
i.e. AP || QC ….(iv) [A – P – B, D – Q – C]
From (iii) and (iv),
□APCQ is a parallelogram. [A quadrilateral is a parallelogram if its opposite sides is parallel and congruent]
Question 2.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.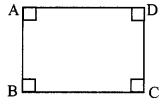
Given:
□ABCD is a rectangle.
To prove: Rectangle ABCD is a parallelogram.
Solution:
Proof:
□ABCD is a rectangle.
∴ ∠A ≅ ∠C = 90° [Given]
∠B ≅ ∠D = 90° [Angles of a rectangle]
∴ Rectangle ABCD is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]
Question 3.
In the adjoining figure, G is the point of concurrence of medians of ADEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that □GEHF is a parallelogram.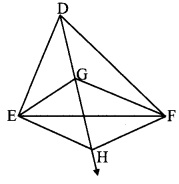
Given: Point G (centroid) is the point of concurrence of the medians of ADEF.
DG = GH
To prove: □GEHF is a parallelogram.
Solution:
Proof:
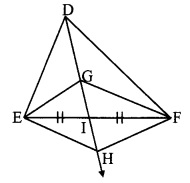
Let ray DH intersect seg EF at point I such that E-I-F.
∴ seg DI is the median of ∆DEF.
∴ El = FI ……(i)
Point G is the centroid of ∆DEF.
![]()
∴ DG = 2(GI)
∴ GH = 2(GI) [DG = GH]
∴ GI + HI = 2(GI) [G-I-H]
∴ HI = 2(GI) – GI
∴ HI = GI ….(ii)
From (i) and (ii),
□GEHF is a parallelogram [A quadrilateral is a parallelogram, if its diagonals bisect each other]
Question 4.
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.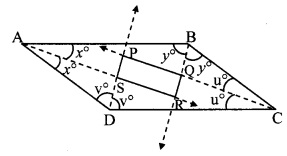
Given: □ABCD is a parallelogram.
Rays AS, BQ, CQ and DS bisect ∠A, ∠B, ∠C and ∠D respectively.
To prove: □PQRS is a rectangle.
Solution:
Proof:
∠BAS = ∠DAS = x° …(i) [ray AS bisects ∠A]
∠ABQ = ∠CBQ =y° ….(ii) [ray BQ bisects ∠B]
∠BCQ = ∠DCQ = u° …..(iii) [ray CQ bisects ∠C]
∠ADS = ∠CDS = v° ….(iv) [ray DS bisects ∠D]
□ABCD is a parallelogram. [Given]
∴ ∠A + ∠B = 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠BAS + ∠DAS + ∠ABQ + ∠CBQ = 180° [Angle addition property]
∴ x°+x°+ v° + v° = 180 [From (i) and (ii)]
∴ 2x° + 2v° =180
∴ x + y = 90° ……(v) [Dividing both sides by 2]
Also, ∠A + ∠D= 180° [Adjacent angles of a parallelogram are supplementary]
∴ ∠BAS + ∠DAS + ADS + ∠CDS = 180° [Angle addition property]
∴ x° + x° + v° + v° = 180°
∴ 2x° + 2v° = 180°
∴ x° + v° = 90° …..(vi) [Dividing both sides by 2]
In ∆ARB,
∠RAB + ∠RBA + ∠ARB = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x° + y° + ∠SRQ = 180° [A – S – R, B – Q – R]
∴ 90° + ∠SRQ = 180° [From (v)]
∴ ∠SRQ = 180°- 90° = 90° …..(vi)
Similarly, we can prove
∠SPQ = 90° …(viii)
In ∆ASD,
∠ASD + ∠SAD + ∠SDA = 180° [Sum of the measures of angles a triangle is 180°]
∴ ∠ASD + x° + v° = 180° [From (vi)]
∴ ∠ASD + 90° = 180°
∴∠ASD = 180°- 90° = 90°
∴ ∠PSR = ∠ASD [Vertically opposite angles]
∴ ∠PSR = 90° …..(ix)
Similarly we can prove
∠PQR = 90° ..(x)
∴ In □PQRS,
∠SRQ = ∠SPQ = ∠PSR = ∠PQR = 90° [From (vii), (viii), (ix), (x)]
∴ □PQRS is a rectangle. [Each angle is of measure 90°]
Question 5.
In the adjoining figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS, then prove that □PQRS is a parallelogram.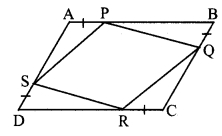
Given: □ABCD is a parallelogram.
AP = BQ = CR = DS
To prove: □PQRS is a parallelogram.
Solution:
Proof:
□ABCD is a parallelogram. [Given]
∴ ∠B = ∠D ….(i) [Opposite angles of a parallelogram]
Also, AB = CD [Opposite sides of a parallelogram]
∴ AP + BP = DR + CR [A-P-B, D-R-C]
∴ AP + BP = DR + AP [AP = CR]
∴ BP = DR ….(ii)
In APBQ and ARDS,
seg BP ≅ seg DR [From (ii)]
∠PBQ ≅ ∠RDS [From (i)]
seg BQ ≅ seg DS [Given]
∴ ∆PBQ ≅ ∆RDS [SAS test]
∴ seg PQ ≅ seg RS …..(iii) [c.s.c.t]
Similarly, we can prove that
∆PAS ≅ ∆RCQ
∴ seg PS ≅ seg RQ ….(iv) [c.s.c.t]
From (iii) and (iv),
□PQRS is a parallelogram. [A quadrilateral is a parallelogram, if pairs of its opposite angles are congruent]
Intext Questions and Activities
Question 1.
Points D and E are the midpoints of side AB and side AC of ∆ABC respectively. Point F is on ray ED such that ED = DF. Prove that □AFBE is a parallelogram. For this example write ‘given’ and ‘to prove’ and complete the proof. (Text book pg. no. 66)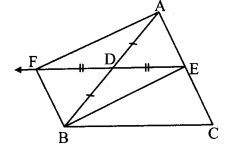
Given: D and E are the midpoints of side AB and side AC respectively.
ED = DF
To prove: □AFBE is a parallelogram.
Solution:
Proof:
seg AB and seg EF are the diagonals of □AFBE.
seg AD ≅ seg DB [Given]
seg DE ≅ seg DF [Given]
∴ Diagonals of □AFBE bisect each other.
∴ □AFBE is a parallelogram. [ By test of parallelogram]