Chapter 5 Quadrilaterals Practice Set 5.5
Chapter 5 Quadrilaterals Practice Set 5.5
Question 1.
In the adjoining figure, points X, Y, Z are the midpoints of of ∆ABC respectively, cm. Find the lengths of side AB, side BC and side AC AB = 5 cm, AC = 9 cm and BC = 11c.m. Find the lengths of XY, YZ, XZ.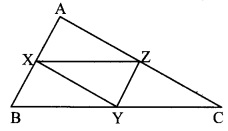
Solution:

Question 2.
In the adjoining figure, □PQRS and □MNRL are rectangles. If point M is the midpoint of side PR, then prove that,
i. SL = LR![]()
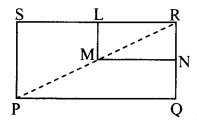
Given: □PQRS and □MNRL are rectangles. M is the midpoint of side PR.
Solution:
Toprove:
i. SL = LR
![]()
Proof:
i. □PQRS and □MNRL are rectangles. [Given]
∴ ∠S = ∠L = 90° [Angles of rectangles]
∠S and ∠L form a pair of corresponding angles on sides SP and LM when SR is their transversal.
∴eg ML || seg PS …(i) [Corresponding angles test]
In ∆PRS,
Point M is the midpoint of PR and seg ML || seg PS. [Given] [From (i)]
∴ Point L is the midpoint of seg SR. ……(ii) [Converse of midpoint theorem]
∴ SL = LR
ii. Similarly for ∆PRQ, we can prove that,
Point N is the midpoint of seg QR. ….(iii)
In ∆RSQ,
Points L and N are the midpoints of seg SR and seg QR respectively. [From (ii) and (iii)]
![]()
Question 3.
In the adjoining figure, ∆ABC is an equilateral triangle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ∆FED is an equilateral triangle.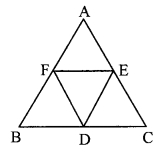
Given: ∆ABC is an equilateral triangle.
Points F, D and E are midpoints of side AB, side BC, side AC respectively.
To prove: ∆FED is an equilateral triangle.
Solution:
Proof:
∆ABC is an equilateral triangle. [Given]
∴ AB = BC = AC ….(i) [Sides of an equilateral triangle]
Points F, D and E are midpoints of side AB and BC respectively.

Question 4.![]()
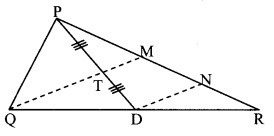
Solution:
Given: seg PD is a median of ∆PQR. Point T is the midpoint of seg PD.
![]()
Construction: Draw seg DN ||seg QM such that P-M-N and M-N-R.
Proof:
In ∆PDN,
Point T is the midpoint of seg PD and seg TM || seg DN [Given]
∴ Point M is the midpoint of seg PN. [Construction and Q-T-M]
∴ PM = MN [Converse of midpoint theorem]
In ∆QMR,
Point D is the midpoint of seg QR and seg DN || seg QM [Construction]
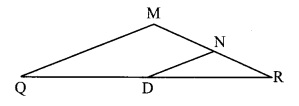
∴ Point N is the midpoint of seg MR. [Converse of midpoint theorem]
∴ RN = MN …..(ii)
∴ PM = MN = RN …..(iii) [From (i) and (ii)]
Now, PR = PM + MN + RN [ P-M-R-Q-T-M]
∴ PR = PM + PM + PM [From (iii) ]
∴ PR = 3PM
![]()