Chapter 5 Sets and Relations Ex 5.2
Chapter 5 Sets and Relations Ex 5.2
Question 1.
If (x – 1, y + 4) = (1, 2), find the values of x and y.
Solution:
(x – 1, y + 4) = (1, 2)
By the definition of equality of ordered pairs, we have
x – 1 = 1 and y + 4 = 2
∴ x = 2 and y = -2
Question 2.
Question 3.
If A = {a, b, c}, B = {x, y}, find A × B, B × A, A × A, B × B.
Solution:
A = (a, b, c}, B = {x, y}
A × B = {(a, x), (a, y), (b, x), (b, y), (c, x), (c, y)}
B × A = {(x, a), (x, b), (x, c), (y, a), (y, b), (y, c)}
A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}
B × B = {(x, x), (x, y), (y, x), (y, y)}
Question 4.
If P = {1, 2, 3} and Q = {1, 4}, find sets P × Q and Q × P.
Solution:
P = {1, 2, 3}, Q = {1, 4}
∴ P × Q = {(1, 1), (1, 4), (2, 1), (2, 4), (3, 1), (3, 4)}
and Q × P = {(1, 1), (1, 2), (1, 3), (4, 1), (4, 2), (4, 3)}
Question 5.
Let A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}. Verify,
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × (B ∪ C) = (A × B) ∪ (A × C)
Solution:
A = {1, 2, 3, 4}, B = {4, 5, 6}, C = {5, 6}
(i) B ∩ C = {5, 6}
A × (B ∩ C) = = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∩ (A × C) = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) B ∪ C = {4, 5, 6}
A × (B ∪ C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3,4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 5), (4, 6)}
∴ (A × B) ∪ (A × C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
∴ A × (B ∪ C) = (A × B) ∪ (A × C)
Question 6.
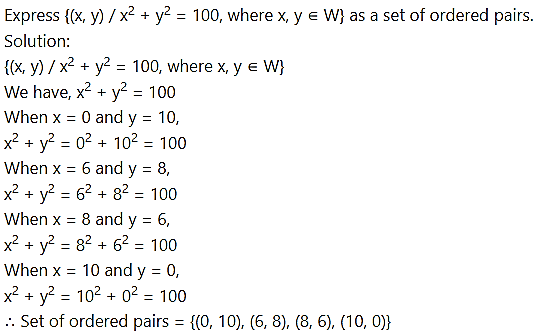
Question 7.
Let A = {6, 8} and B = {1, 3, 5}. Show that R1 = {(a, b) / a ∈ A, b ∈ B, a – b is an even number} is a null relation, R2 = {(a, b) / a ∈ A, b ∈ B, a + b is an odd number} is a universal relation.
Solution:
A = {6, 8}, B = {1, 3, 5}
R1 = {(a, b)/ a ∈ A, b ∈ B, a – b is an even number}
a ∈ A
∴ a = 6, 8
b ∈ B
∴ b = 1, 3, 5
When a = 6 and b = 1, a – b = 5, which is odd
When a = 6 and b = 3, a – b = 3, which is odd
When a = 6 and b = 5, a – b = 1, which is odd
When a = 8 and b = 1, a – b = 7, which is odd
When a = 8 and b = 3, a – b = 5, which is odd
When a = 8 and b = 5, a – b = 3, which is odd
Thus, no set of values of a and b gives a – b as even.
∴ R1 has a null relation from A to B.
A × B = {(6, 1), (6, 3), (6, 5), (8, 1), (8, 3), (8, 5)}
When a = 6 and b = 1, a + b = 7, which is odd
When a = 6 and b = 3, a + b = 9, which is odd
When a = 6 and b = 5, a + b = 11, which is odd
When a = 8 and b = 1, a + b = 9, which is odd
When a = 8 and b = 3, a + b = 11, which is odd
When a = 8 and b = 5, a + b = 13, which is odd
∴ R2 = {(6, 1), (6, 3), (6, 5), (8, 1), (8, 3), (8, 5)}
Here, R2 = A × B
∴ R2 has a universal relation from A to B.
Question 8.
Write the relation in the Roster form. State its domain and range.

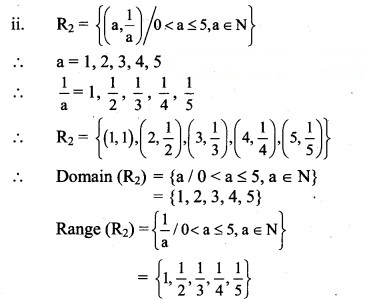
(iii) R3 = {(x, y) / y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
Here y = 3x
When x = 1, y = 3(1) = 3
When x = 2, y = 3(2) = 6
When x = 3, y = 3(3) = 9
∴ R3 = {(1, 3), (2, 6), (3, 9)}
∴ Domain (R3) ={1, 2, 3}
∴ Range (R3) = {3, 6, 9}
(iv) R4 = {(x, y) / y > x + 1, x = 1, 2 and y = 2, 4, 6}
Here, y > x + 1
When x = 1 and y = 2, 2 ≯ 1 + 1
When x = 1 and y = 4, 4 > 1 + 1
When x = 1 and y = 6, 6 > 1 + 1
When x = 2 and y = 2, 2 ≯ 2 + 1
When x = 2 and y = 4, 4 > 2 + 1
When x = 2 and y = 6, 6 > 2 + 1
∴ R4 = {(1, 4), (1, 6), (2, 4), (2, 6)}
Domain (R4) = {1, 2}
Range (R4) = {4, 6}
(v) R5 = {{x, y) / x + y = 3, x, y ∈ (0, 1, 2, 3)}
Here, x + y = 3
When x = 0, y = 3
When x = 1, y = 2
When x = 2, y = 1
When x = 3, y = 0
∴ R5 = {(0, 3), (1, 2), (2, 1), (3, 0)}
Domain (R5) = {0, 1, 2, 3}
Range (R5) = {3, 2, 1, 0}
(vi) R6 = {(a, b)/ a ∈ N, a < 6 and b = 4}
a ∈ N and a < 6
∴ a = 1, 2, 3, 4, 5 and b = 4
R6 = {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4)}
Domain (R6) = {1, 2, 3, 4, 5}
Range (R6) = {4}
(vii) R7 = {(a, b) / a, b ∈ N, a + b = 6}
Here, a + b = 6
When a = 1, b = 5
When a = 2, b = 4
When a = 3, b = 3
When a = 4, b = 2
When a = 5, b = 1
∴ R7 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
Domain (R7) = {1, 2, 3, 4, 5}
Range (R7) = {5, 4, 3, 2, 1}
(viii) R8 = {(a, b) / b = a + 2, a ∈ Z, 0 < a < 5}
Here, b = a + 2
When a = 1, b = 3
When a = 2, b = 4
When a = 3, b = 5
When a = 4, b = 6
∴ R8 = {(1, 3), (2, 4), (3, 5), (4, 6)}
Domain (R8) = {1, 2, 3, 4}
Range (R8) = {3, 4, 5, 6}
Question 9.
Identify which of the following relations are reflexive, symmetric, and transitive.
Solution:

(i) Given, R = {(a, b): a, b ∈ Z, a – b is an integer}
Let a ∈ Z, then a – a ∈ Z
∴ (a, a) ∈ R
∴ R is reflexive.
Let (a, b) ∈ R
∴ a – b ∈ Z
∴ -(a – b) ∈ Z, i.e., b – a ∈ Z
∴ (b, a) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ a – b ∈ Z and b – c ∈ Z
∴ (a – b) + (b – c) ∈ Z
∴ a – c ∈ Z
∴ (a, c) ∈ R
∴ R is transitive.
(ii) Given, R = {(a, b) : a, b ∈ N, a + b is even}
Let a ∈ N, then a + a = 2a, which is even.
∴ (a, a) ∈ R
∴ R is reflexive.
Let (a, b) ∈ R
∴ a + b is even
∴ b + a is even
∴ (b, a) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ a + b and b + c is even
Let a + b = 2x and b + c = 2y for x, y ∈ N
∴ (a + b) + (b + c) = 2x + 2y
∴ a + 2b + c = 2(x + y)
∴ a + c = 2(x + y) – 2b = 2(x + y – b)
∴ a + c is even ……..[∵ x, y, b ∈ N, x + y – b ∈ N]
∴ (a, c) ∈ R
∴ R is transitive.
(iii) Given, R = {(a, b) : a, b ∈ N, a divides b}
Let a ∈ N, then a divides a.
∴ (a, a) ∈ R
∴ R is reflexive.
Let a = 2 and b = 8, then 2 divides 8
∴ (a, b) ∈ R
But 8 does not divide 2.
∴ (b, a) ∉ R
∴ R is not symmetric.
Let (a, b) and (b, c) ∈ R
∴ a divides b and b divides c.
Let b = ax and c = by for x, y ∈ N.
∴ c = (ax) y = a(xy)
i.e., a divides c.
∴ (a, c) ∈ R
∴ R is transitive.
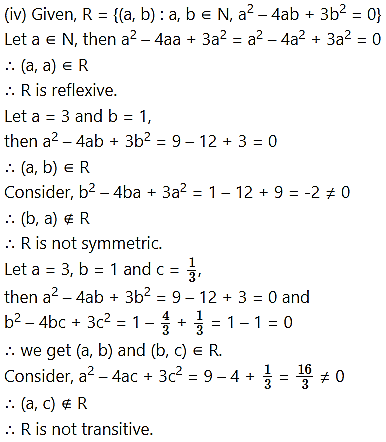
(v) Given, R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls}
Let a ∈ G, then ‘a’ cannot be a sister of herself.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let (a, b) ∈ R
∴ ‘a’ is a sister of ‘b’.
∴ ‘b’ is a sister of ‘a’.
∴ (b, c) ∈ R
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R
∴ ‘a’ is a sister of ‘b’ and ‘b’ is a sister of ‘c’
∴ ‘a’ is a sister of ‘c’.
∴ (a, c) ∈ R
∴ R is transitive.
(vi) Given, R = {(a, b) : Line a is perpendicular to line b in a plane}
Let a be any line in the plane, then a cannot be perpendicular to itself.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let (a, b) ∈ R
∴ a is perpendicular to b.
∴ b is perpendicular to a.
∴ (b, a) ∈ R.
∴ R is symmetric.
Let (a, b) and (b, c) ∈ R.
∴ a is perpendicular to b and b is perpendicular to c.
∴ a is parallel to c.
∴ (a, c) ∉ R
∴ R is not transitive.
(vii) Given, R = {(a, b) : a, b ∈ R, a < b}
Let a ∈ R, then a ≮ a.
∴ (a, a) ∉ R
∴ R is not reflexive.
Let a = 1 and b = 2, then 1 < 2
∴ (a, b) ∈ R
But 2 ≮ 1
∴ (b, a) ∉ R
∴ R is not symmetric.
Let (a, b) and (b, c) ∈ R
∴ a < b and b < c
∴ a < c
∴ (a, c) ∈ R
∴ R is transitive.
