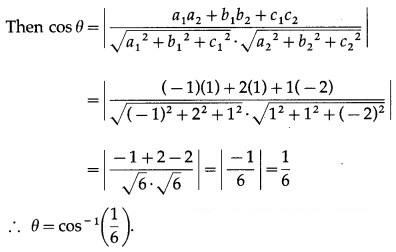Blog

Chapter 5 Vectors Ex 5.3

Chapter 5 Vectors Ex 5.3

Question 1.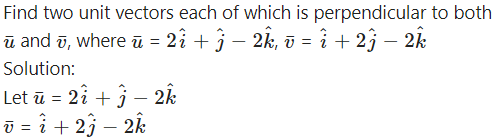

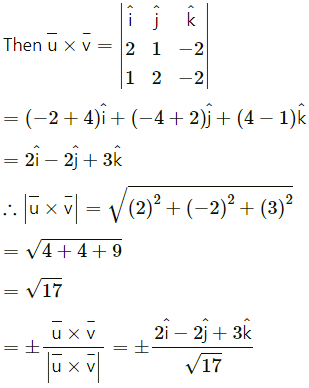
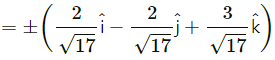
Question 2.


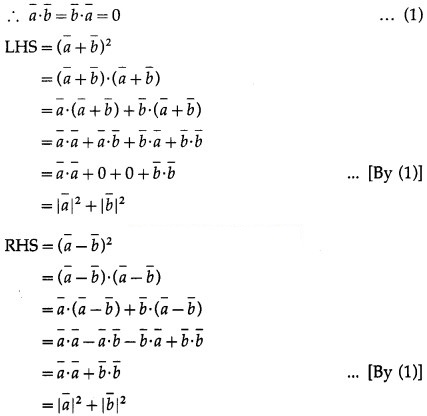
∴ LHS = RHS
Hence, (a¯ + b¯)² = (a¯ – b¯)².

Question 3.


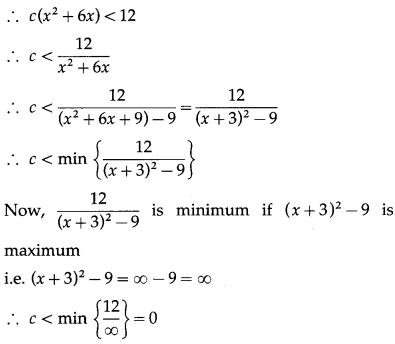
∴ c < 0.
Hence, the angle between a and b is obtuse if c < 0.

Question 4.

Question 5.
Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular.
Solution:

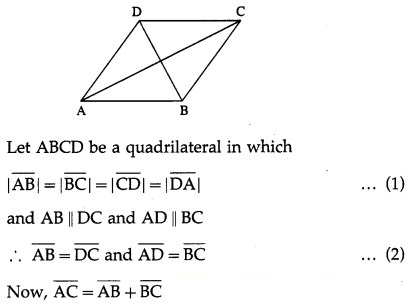
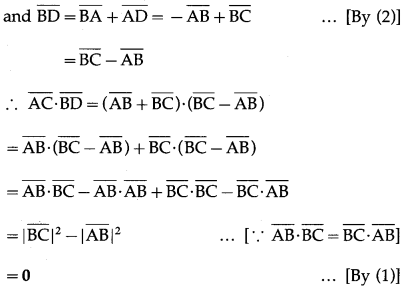
Question 6.

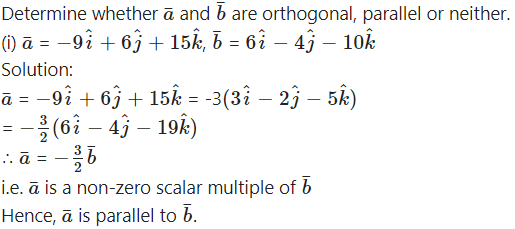
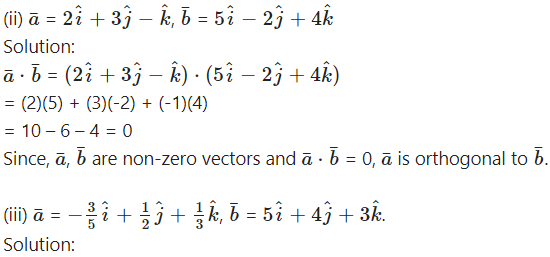
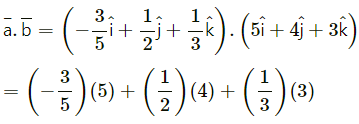
= -3 + 2 + 1
= 0

Question 7.
Find the angle P of the triangle whose vertices are P(0, -1, -2), Q(3, 1, 4) and R(5, 7, 1).
Solution:



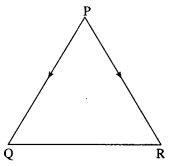
∴ P = 45°

Question 8.

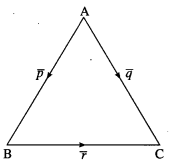
Solution:

Question 9.
Prove by vector method that the angle subtended on semicircle is a right angle.
Solution:


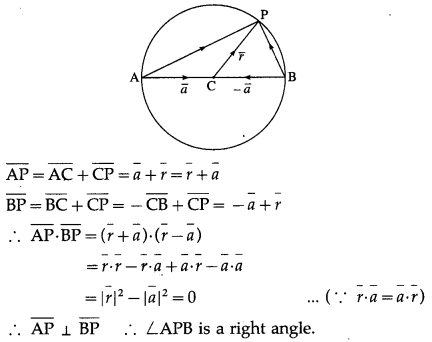
Hence, the angle subtended on a semicircle is the right angle.

Question 10.
If a vector has direction angles 45ºand 60º find the third direction angle.
Solution:
Let α = 45°, β = 60°
We have to find γ.
∴ cos²α + cos²β + cos²γ = 1
∴ cos²45° + cos²60° + cos²γ = 1

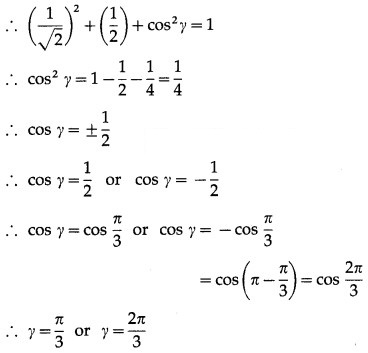
Question 11.
If a line makes angles 90º, 135º, 45º with the X, Y and Z axes respectively, then find its direction cosines.
Solution:
Let l, m, n be the direction cosines of the line.
Then l = cos α, m = cos β, n = cos γ
Here, α = 90°, β = 135° and γ = 45°
∴ l = cos 90° = 0

Question 12.
If a line has the direction ratios, 4, -12, 18 then find its direction cosines.
Solution:
The direction ratios of the line are a = 4, b = -12, c = 18.
Let l, m, n be the direction cosines of the line.

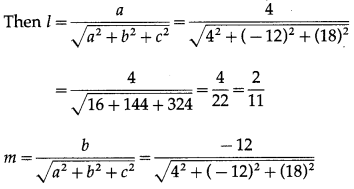
Question 13.


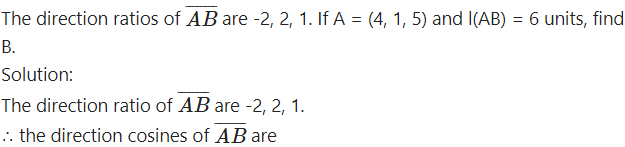
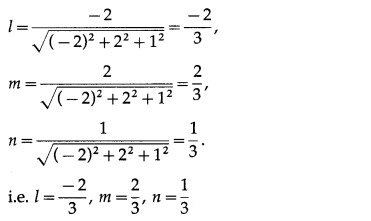
The coordinates of the points which are at a distance of d units from the point (x₁, y₁, z₁) are given by (x₁ ± ld, y₁ ± md, z₁ ± nd)

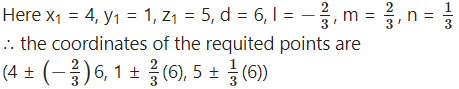
i.e. (4 – 4, 1 + 4, 5 + 2) and (4 + 4, 1 – 4, 5 – 2)
i.e. (0, 5, 7) and (8, -3, 3).

Question 14.
Find the angle between the lines whose direction cosines l, m, n satisfy the equations 5l + m + 3n = 0 and 5mn – 2nl + 6lm = 0.
Solution:
Given, 5l + m + 3n = 0 …(1)
and 5mn – 2nl + 6lm = 0 …(2)
From (1), m = -(51 + 3n)
Putting the value of m in equation (2), we get,
-5(5l + 3n)n – 2nl – 6l(5l + 3n) = 0
∴ -25ln – 15n² – 2nl – 30l² – 18ln = 0
∴ – 30l² – 45ln – 15n² = 0
∴ 2l² + 3ln + n² = 0
∴ 2l² + 2ln + ln + n² = 0
∴ 2l(l + n) + n(l + n) = 0
∴ (l + n)(2l + n) = 0
∴ l + n = 0 or 2l + n = 0
l = -n or n = -2l
Now, m = -(5l + 3n), therefore, if l = -n,
m = -(-5n + 3n) = 2n

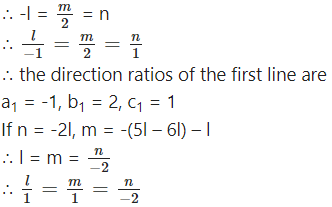
∴ the direction ratios of the second line are
a₂ = -1, b₂ = 1, c₂ = -2
Let θ be the angle between the lines.