Blog

Chapter 8 Trigonometry Practice Set 8.2

Chapter 8 Trigonometry Practice Set 8.2

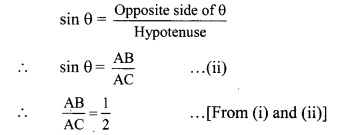
Question 1.
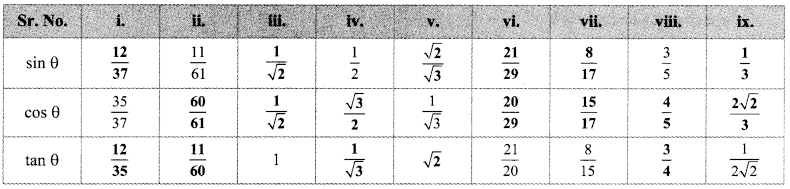
In the following table, a ratio is given in each column. Find the remaining two ratios in the column and complete the table.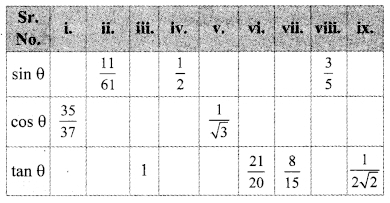

Solution:

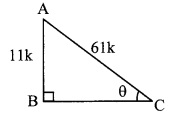
In right angled ∆ABC,

∠C = θ.

Let the common multiple be k.
∴ BC = 35k and AC = 37k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (37k)² = AB²+ (35k)²
1369k² = AB² + 1225k²
AB2 = 1369k² – 1225k²
= 144k²
AB = 144k²

= 12k

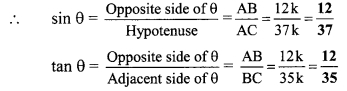
In right angled ∆ABC, ∠C = θ.


Let the common multiple be k.
AB = 11k and AC = 61k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (61k)² = (11k)² + BC²
∴ 3721k² = 121k² + BC²
∴ BC² = 3721k² – 121k² = 3600k²

= 60k

In right angled ∆ABC,
∠C = θ.


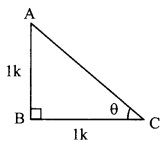
Let the common multiple be k.
∴ AB = 1k and BC = 1k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= K² + K²
= 2K²
∴ AC = \(\sqrt { 2{ k }\)

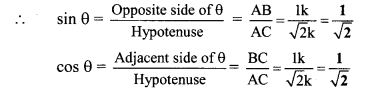
In right angled ∆ABC,
∠C = θ.


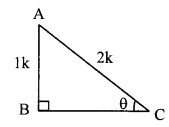
Let the common multiple be k.
∴ AB = 1k and BC = 2k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ 2K² = K² + BC²
∴ 4K² = K² + BC²
∴ BC² = 4K² – K² = 3K²

= \(\sqrt { 3{ k }\)

In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
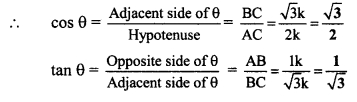
∴ AB = 1k and BC = √3k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (√3K)² = AB² + K²
∴ 3K² = 3K² – K² = 2K²

AB = √2K

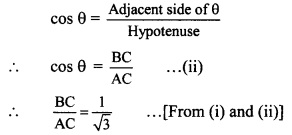
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 21k and BC = 20k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= (21)K² + (20K)²
= 441K² – 400²
= 841K²

= 29K

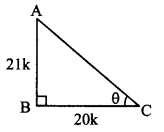
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 8k and BC = 15k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= (8)K² + (15K)²
= 64K² – 225²
= 289K²

= 17K

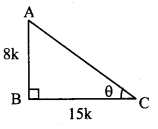
In right angled ∆ABC,
∠C = θ.



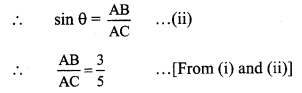
Let the common multiple be k.
∴ AB = 3k and AC = 5k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (5)K²= (3)K² + BC²
∴ 25K² = 9K² – 225²
∴ BC² = 25K² – 9K²

= 4K

In right angled ∆ABC,
∠C = θ.


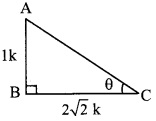
Let the common multiple be k.
∴ AB = 1k and AC = 2√2 k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= K² + (2√2 k )²
= K² – 225²
= 25K² + 8K²
= 9K²

= 3K

Question 2.
Find the values of:
i. 5 sin 30° + 3 tan 45°
ii. 45tan² 60° + 3 sin² 60°
iii. 2 sin 30° + cos 0° + 3 sin 90°

v. cos² 45° + sin² 30°
vi. cos 60° x cos 30° + sin 60° x sin 30°
Solution:
i. sin 30° = 1/2 and tan 45° = 1

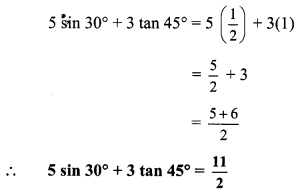
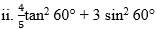
iii. 2 sin 30° + cos 0° + 3 sin 90°

= 1 + 1 + 3
∴ 2 sin 30° + cos 0° + 3 sin 90° = 5

v. cos² 45° + sin² 30°

vi. cos 60° x cos 30° + sin 60° x sin 30°

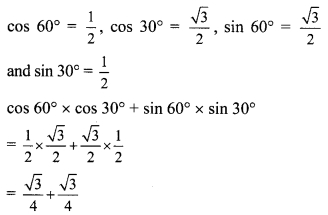
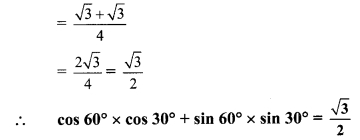
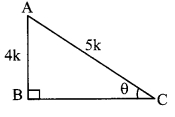
Question 3.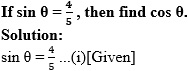

In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 4k and AC = 5k
Now, AC² = AB² + BC² … [Pythagoras theorem]
∴ (5 k)² = (4k)² + BC²
∴ 25k² = 16k² + BC²
∴ BC² = 25k² – 16k² = 9k²

= 3k

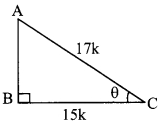
Question 4.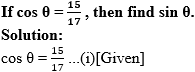

In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ BC = 15k and AC = 17k
Now, AC² = AB² + BC² … [Pythagoras theorem]
∴ (17 k)² = AB² + (15K)²
∴ 289k² = AB² + 225²
∴ AB² = 289k² – 225k²
= 64k²

= 8k

Intext Questions and Activities

Question 1.
In right angled ∆PQR, ∠Q = 900. Therefore ∠P and ∠R are complementary angles of each other. Verify the following ratios.
i. sin θ = cos (90 – θ)
ii. cos θ = sin (90 – θ)
iii. sin 30° = cos (90° – 30°) = cos 60°
iv. cos 30° = sin (90° – 30°) = sin 60° (Textbook pg. no. 107)
Solution:
In ∆PQR, ∠Q = 90°, ∠P = θ
∴ ∠R = 90 – θ

i. sin θ = cos (90 – θ)

ii. cos θ = sin (90 – θ)

iii. Let ∠P = θ = 30°
∴ ∠R = 90° – 30°

sin 30° = cos (90° – 30°) … [From (i) and (ii)]
sin 30° = cos 60°

iv. cos 30° = sin (90° – 30°) = sin 60°

∴ cos 30° = sin (90° – 30°) .,.[From (i) and (ii)]
∴ cos 30° = sin 60°

Question 2.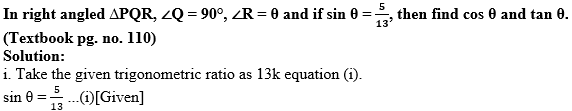

By using the definition write the trigonometric ratio of sin O and take it as equation (ii).
In right angled ∆PQR, ∠R = θ


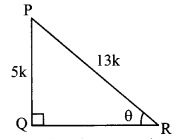
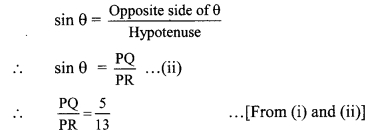
Let the common multiple be k.
∴ PQ = 5k and PR = 13k
Find QR by using Pythagoras theorem.
PR² = PQ² + QR² … [Pythagoras theorem]
∴ (13k)² = (5k)² + QR²
∴ 169k² = 25k² + QR²
∴ QR² = 169k² – 25k²
= 144k²

= 12k

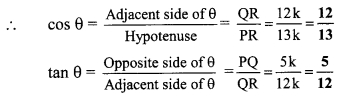
Question 3.
While solving the above Illustrative example, why the lengths of PQ and PR are taken 5k and 13k? (Textbook pg. no. 111)
Solution:

Here, the ratio of the lengths of sides PQ and PR is 5 : 13.
The actual lengths of the sides can be any multiple of the ratio. Hence, we consider the multiple k while solving.

Question 4.
While solving the above illustrative example, can we take the lengths of PQ and PR as 5 and 13? If so, then what changes are needed In the writing of the solution. (Tcxtbook pg. no. 111)
Solution:
Yes, we can take lengths of PQ and PR as 5 and 13.
In that case, we will have to take k = 1 and solve the problem accordingly.

Question 5.
Verify that the equation ‘sin² θ + cos² θ = 1’ is true when θ = 0° or θ = 90°.
(Textbook pg. no. 112)
Solution:
sin² θ + cos² θ = 1
i. lf θ = 0°,
LH.S. = sin² θ + cos² θ
= sin² 0° + cos² 0°
= 0 + 1 …[∵ sin 0° = 0, cos 0° = 1]
= R.H.S.
∴ sin² θ + cos² θ = 1

ii. If θ = 90°,
L.H.S.= sin² θ +cos² θ
= sin² 90° + cos² 90°
= 1 + 0 … [ ∵ sin 90° = 1, cos 90° = 0]
= 1
= R.H.S.
∴ sin² θ + cos² θ = 1