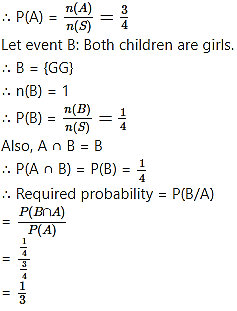Chapter 9 Probability Ex 9.3
Chapter 9 Probability Ex 9.3
Question 1.
A bag contains 3 red marbles and 4 blue marbles. Two marbles are drawn at random without replacement. If the first marble drawn is red, what is the probability that the second marble is blue?
Solution:

Alternate Method:

Question 2.
A box contains 5 green pencils and 7 yellow pencils. Two pencils are chosen at random from the box without replacement. What is the probability that both are yellow?
Solution:

Question 3.
In a sample of 40 vehicles, 18 are red, 6 are trucks, of which 2 are red. Suppose that a randomly selected vehicle is red. What is the probability it is a truck?
Solution:
One vehicle is selected from 40 vehicles.
Let event A: The selected vehicle is red.

Question 4.
From a pack of well-shuffled cards, two cards are drawn at random. Find the probability that both the cards are diamonds when
(i) the first card drawn is kept aside.
(ii) the first card drawn is replaced in the pack.
Solution:

Question 5.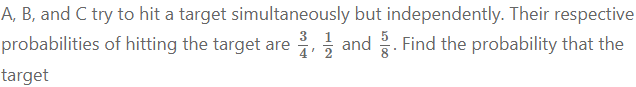
(a) is hit exactly by one of them.
(b) is not hit by any one of them.
(c) is hit.
(d) is exactly hit by two of them.
Solution:
Let event A: A can hit the target,
event B: B can hit the target,
event C: C can hit the target.
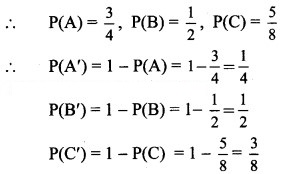
Since A, B, C are independent events,
A’, B’, C’ are also independent events.
(a) Let event W: Target is hit exactly by one of them.
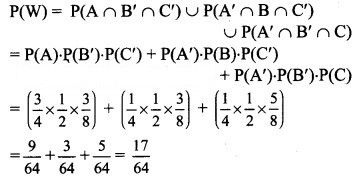
(b) Let event X: Target is not hit by any one of them.
∴ P(X) = P(A’ ∩ B’ ∩ C’)
= P(A’) P(B’) P(C’)
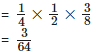
(c) Let event Y: Target is hit.
∴ P(Y) = 1 – P(target is not hit by any one of them)
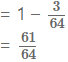
(d) Let event Z: Target is hit by exactly two of them.
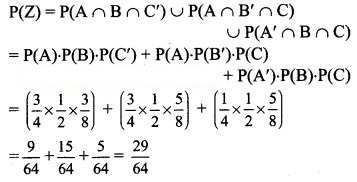
Question 6.
The probability that a student X solves a problem in dynamics is 2/5 and the probability that student Y solves the same problem is 1/4. What is the probability that
(i) the problem is not solved?
(ii) the problem is solved?
(iii) the problem is solved exactly by one of them?
Solution:


Question 7.
A speaks truth in 80% of the cases and B speaks truth in 60% of the cases. Find the probability that they contradict each other in narrating an incident.
Solution:

Question 8.
Two hundred patients who had either Eye surgery or Throat surgery were asked whether they were satisfied or unsatisfied regarding the result of their surgery. The following table summarizes their response.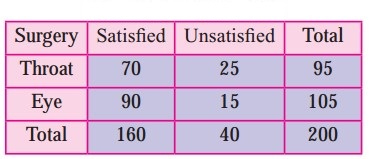
If one person from the 200 patients is selected at random, determine the probability
(a) that the person was satisfied given that the person had Throat surgery.
(b) that person was unsatisfied given that the person had eye surgery.
(c) the person had Throat surgery given that the person was unsatisfied.
Solution:
(a) Let event A: The patient was satisfied,
event B: The patient had throat surgery.
Given, n(S) = 200

(b) Let event C : The patient was unsatisfied,
event D : The patient had a eye surgery.
Given, n(S) = 200
n(C ∩ D) = 15

Question 9.
Two dice are thrown together. Let A be the event ‘getting 6 on the first die’ and B be the event ‘getting 2 on the second die’. Are events A and B independent?
Solution:
When two dice are thrown, the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
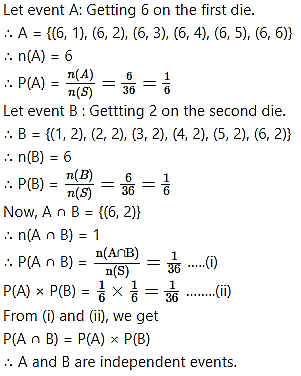
Question 10.
The probability that a man who is 45 years old will be alive till he becomes 70 is 5/12. The probability that his wife who is 40 years old will be alive till she becomes 65 is 3/8. What is the probability that, 25 years hence,
(a) the couple will be alive?
(b) exactly one of them will be alive?
(c) none of them will be alive?
(d) at least one of them will be alive?
Solution:


Question 11.
A box contains 10 red balls and 15 green balls. Two balls are drawn in succession without replacement. What is the probability that,
(a) the first is red and the second is green?
(b) one is red and the other is green?
Solution:
Total number of balls = 10 + 15 = 25

Question 12.
A bag contains 3 yellow and 5 brown balls. Another bag contains 4 yellow and 6 brown balls. If one ball is drawn from each bag, what is the probability that,
(a) both the balls are of the same colour?
(b) the balls are of a different colours?
Solution:

Question 13.
An urn contains 4 black, 5 white, and 6 red balls. Two balls are drawn one after the other without replacement. What is the probability that at least one of them is black?
Solution:

Question 14.
Three fair coins are tossed. What is the probability of getting three heads given that at least two coins show heads?
Solution:
When three fair coins are tossed, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
∴ n(S) = 8
Let event A: Getting three heads.
∴ A = {HHH}
Let event B: Getting at least two heads.
∴ B = {HHT, HTH, THH, HHH}

Question 15.
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards are drawn are face cards?
Solution:

Question 16.
Bag A contains 3 red and 2 white balls and bag B contains 2 red and 5 white balls. A bag is selected at random, a ball is drawn and put into the other bag, and then a ball is drawn from that bag. Find the probability that both the balls are drawn are of the same colour.
Solution:

Let event X: Both the balls drawn are of same colour.
∴ P(X) = P(G) × P (X/G) + P(H) × P(X/H) …….(i)

Question 17.
Activity: A bag contains 3 red and 5 white balls. Two balls are drawn at random one after the other without replacement. Find the probability that both the balls are white.
Solution:

Question 18.
A family has two children. Find the probability that both the children are girls, given that at least one of them is a girl.
Solution:
A family has two children.
∴ Sample space S = {BB, BG, GB, GG}
∴ n(S) = 4
Let event A: At least one of the children is a girl.
∴ A = {GG, GB, BG}
∴ n(A) = 3