02 Mechanical Properties of Fluids
Multiple Choice Questions
1. Absorption of water by filter paper is due to ………………………
(A) cohesion
(B) capillarity
(C) adhesion
(D) elasticity
Ans. (B) capillarity
2. ‘
( = Surface tension of water
(A)
(B)
(C)
(D)
Ans. (A)
3. A big drop of radius is formed from 1000 droplets of water. The radius of a droplet will be
(A)
(B)
(C)
(D)
Ans. (B)
4. In which of the following substances, surface tension increases with increase in temperature?
(A) Copper
(B) Molten copper
(C) Iron
(D) Molten iron
Ans. (B) Molten copper
5. Angle of contact for the pair of pure water with clean glass is ………………………
(A) acute
(B) obtuse
(C)
(D)
Ans. (D)
6. If two capillary tubes of different diameters are partially dipped in the same liquid vertically, then the rise of liquid
(A) is same in both the tubes.
(B) is more in the tube of larger diameter.
(C) will not be in smaller diameter tube.
(D) is more in the tube of smaller diameter.
Ans. (D) is more in the tube of smaller diameter.
7. tiny mercury droplets coalesce to form a bigger drop. In this process, temperature of the drop ………………………
(A) increases
(B) may increase or decrease
(C) decreases
(D) does not change
Ans. (A) increases
8. A rectangular film of a liquid is long and
wide. If the work done in increasing its area to
is
, the surface tension of the solution is:
(A)
(B)
(C)
(D)
Ans. (D)
9. When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
(A) increases
(B) decreases
(C) remains constant
(D) becomes infinite
Ans. (B) decreases
10. Two droplets coalesce in a single drop. In this process ………………………
(A) energy is liberated
(B) energy is absorbed
(C) energy does not change
(D) some mass is converted into energy
Ans. (A) energy is liberated
11. A liquid rises in glass capillary tube upto a height of at room temperature. If another glass capillary tube ‘having radius half that of the earlier tube is immersed in the same liquid, the rise of liquid in it will be ………………………
(A)
(B)
(C)
(D)
Ans. (C)
12. Raindrops are spherical in shape because of ………………………
(A) surface tension
(B) capillarity
(C) downward motion
(D) acceleration due to gravity
Ans. (A) surface tension
13. If ‘ ‘ represents the angle of contact made by a liquid which completely wets the surface of the container then ………………………
(A)
(B)
(C)
(D)
Ans. (A)
Theory Questions
- Surface tension
1. Define the terms:
i. sphere of influence ii. angle of contact
Ans:
i. An imaginary sphere with a molecule at its centre and radius equal to the molecular range is called the sphere of influence of the molecule.
ii. The angle of contact between a liquid and a solid surface is defined as the angle between the tangents drawn to the free surface of the liquid and surface of the solid at the point of contact, measured within the liquid.
2. Define surface tension. Explain the effect of impurity on surface tension.
Ans: Surface tension:
Surface tension is defined as the tangential force acting per unit length on both sides of an imaginary line drawn on the free surface of liquid. Effect of impurities on surface tension:
The effect of impurities on surface tension of liquid can be either due to soluble impurities or insoluble impurities on the surface of liquid.
i. Effect of soluble impurities:
When soluble substance such as common salt (i.e., sodium chloride) is dissolved in water, the surface tension of water increases.
ii. Effect of partly soluble impurities:
When a sparingly soluble substance such as phenol or a detergent is mixed with water, surface tension of water decreases.
Example: a detergent powder is mixed with water to wash clothes. Due to this, the surface tension of water decreases and water makes good contact with the fabric and is able to remove tough stains.
iii. Effect of insoluble impurities:
When insoluble impurity is added into water, surface tension of water decreases. When impurity gets added to any liquid, the cohesive force of that liquid decreases which affects the meniscus. If mercury gathers dust then its surface tension is reduced. It does not form spherical droplets unless the dust is completely removed.
3. Define surface tension. State its S.I. unit and dimensions.
[Mar 09]
Ans: Refer Subtopic 2.4: Q. No. 2 (Definition only)
i Unit: or J/m in SI system.
ii. Dimensions:
4. Obtain the relation between surface energy and surface tension.
OR
Show that the surface tension of a liquid is erically equal to the surface energy per unit aren.
OR
Daive the relation between surface tension and surface energy per unit area.
Ans: Relation between surface tension and surface energy per unit area:
i. Let be a rectangular frame of wire, fitted with a movable arm
.
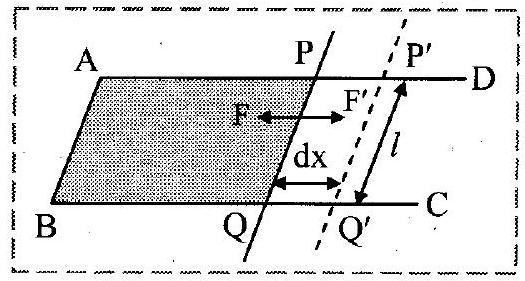
ii. The frame held in horizontal position is dipped into soap solution and taken out so that a soap film APQB is formed. Due to surface tension of soap solution, a force ‘ ‘ will act on each arm of the frame. Under the action of this force, the movable arm PQ moves towards AB.
iii. Magnitude of force due to surface tension is,
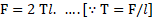
(A factor of 2 appears because soap film has two surfaces which are in contact with wire.)
iv. Let the wire be pulled outwards through a small distance ‘
‘ to the position
, by applying an external force
isothermally, which is equal and opposite to
. Work done by this force,
.
v. But, increase in area of two surfaces of film.
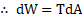
vi. This work done in stretching the film is stored in the area in the form of potential energy (surface energy).
Surface energy,
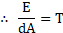
Hence, surface tension = surface energy per unit area.
vii Thus, surface tension is equal to the mechanical work done per unit surface area of the liquid, which is also called as surface energy.
5. Explain the rise of liquid in the capillary on the basis of pressure difference.
Ans: Explanation of capillary action:

i. Suppose a capillary tube is dipped into water.
ii. Consider the situation before the movement of water inside the capillary. The shape of the surface of water in the capillary is concave.
iii. Let us consider four points as shown in the figure. Point is just above the concave surface inside the capillary. B is just below the concave surface inside the capillary.
is just above the plane surface outside the capillary.
is just below the plane surface outside the capillary and is at the same horizontal level as that of
.
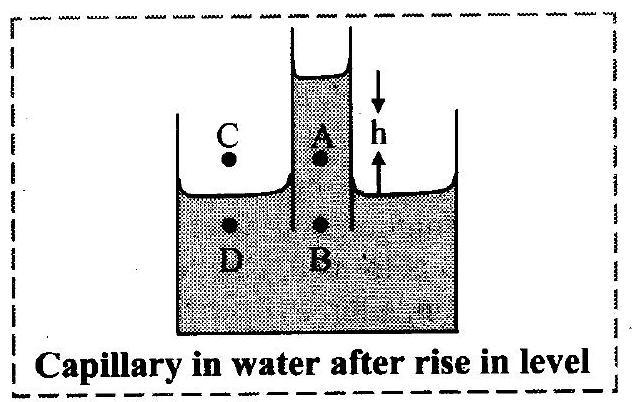
iv. Let and
be the pressures at points
and
respectively.
v. Since pressure on concave side of liquid surface is greater than that on the convex side.
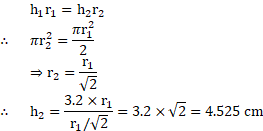
vi. As the pressure is same on both sides of a plane surface,
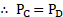
vii. The points and
are at the same level, the pressure at both these points is the same.
atmospheric pressure
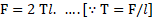
viii. But points and
are at same horizontal level in the liquid. Therefore, in order to maintain the same pressure, the liquid out of the capillary flows into the capillary tube and rises above the point
, till the pressure at
becomes the same as that at
. Because of this, there is a rise in the level of liquid inside the capillary tube.
6. Define angle of contact. State any two properties of angle of contact.
OR
Define the angle of contact and state it’s any ‘two’ characteristics.
Ans: Refer Subtopic 2.4: Q. No. 1 (ii)
Properties of angle of contact:
i. The angle of contact is constant for a given liquid-solid pair.
ii. The value of angle of contact depends upon nature of liquid and solid in contact.
iii. It depends upon the medium which exists above the free liquid surface.
iv. The angle of contact changes due to impurity or temperature.
v. A small contamination of the surface causes a large change in the angle of contact.
[Any two properties]
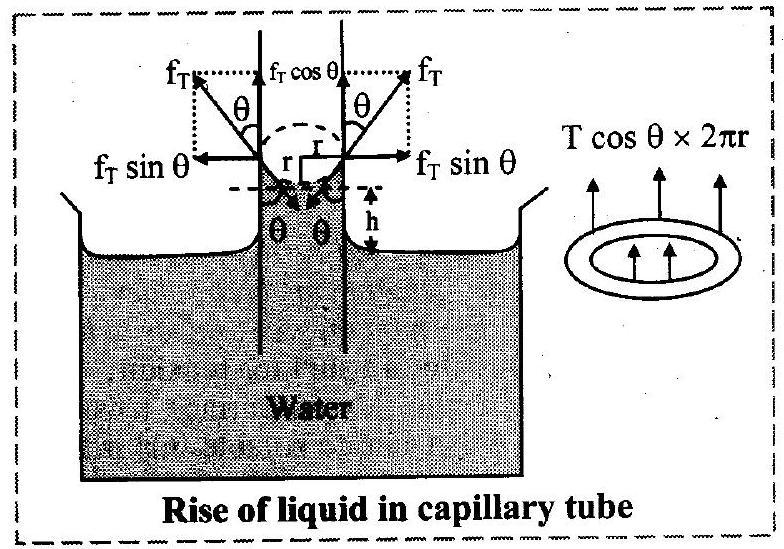
7. Draw a neat labelled diagram of rise of liquid in capillary tube showing different components of tension (force).
OR
Draw a neat labelled diagram showing forces acting on the meniscus of water in a capillary tube.
OR
Draw a neat diagram for the rise of liquid in a capillary tube showing the components of a surface tension.
Ans:
8. Derive Laplace’s law for a spherical membrane.
OR
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
OR
Derive an expression for excess pressure inside a drop of liquid.
Ans: Expression for excess pressure inside a drop:
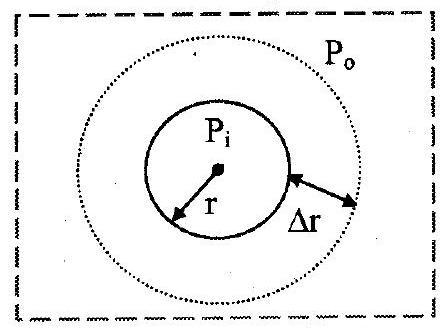
i. Free surface of drops or bubbles are spherical in shape.
Let,
inside pressure of a drop or air bubble
outside pressure of bubble
radius of drop or bubble.
ii. As drop is spherical,
excess pressure inside drop
iii. Let the radius of drop increases from to
so that inside pressure remains constant.
iv. Initial area of drop ,
Final surface area of drop
Increase in surface area,
v. As is very small, the term containing
can be neglected.
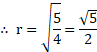
vi. Work done by force of surface tension,
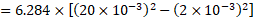
This work done is also equal to the product of the force which causes increase in the area of the bubble and the displacement
which is the increase in the radius of the bubble.
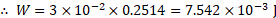
The excess force is given by,
(Excess pressure) Surface area)
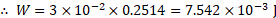
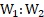
From equation (1),
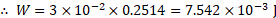
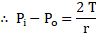
Equation (2) represents excess pressure inside a drop or air bubble. It is also called Laplace’s law of spherical membrane.
vii. In case of soap bubble, there are two free surfaces in contact with air.
For a bubble,
Total increase in the surface area of a soap bubble, while increasing its radius by , is
The work done by this excess pressure is
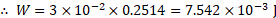
Excess pressure,
9. Draw a neat, labelled diagram for a liquid surface in contact with a solid, when the angle of contact is acute.
Ans:
10. Define surface tension and surface energy.
Ans:
i Refer Subtopic 2.4: Q. No. 2 (Definition only) ii. Surface energy:
The extra energy of the molecules on the surface layer of a liquid is called surface energy of the liquid.
11. Obtain an expression for the rise of a liquid in a capillary tube.
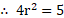
Derive an expression for height of liquid column when a capillary tube is vertically dipped in a liquid.
Ans: Expression for capillary rise:
i. When glass capillary tube is dipped into a liquid, then the liquid rises in the capillary against gravity.
Hence, the weight of the liquid column must be equal and opposite to the component of force due to surface tension at the point of contact.
ii. The length of liquid in contact inside the capillary is the circumference .
Let, radius of capillary tube
height of liquid level in the tube
surface tension of liquid
density of liquid
acceleration due to gravity
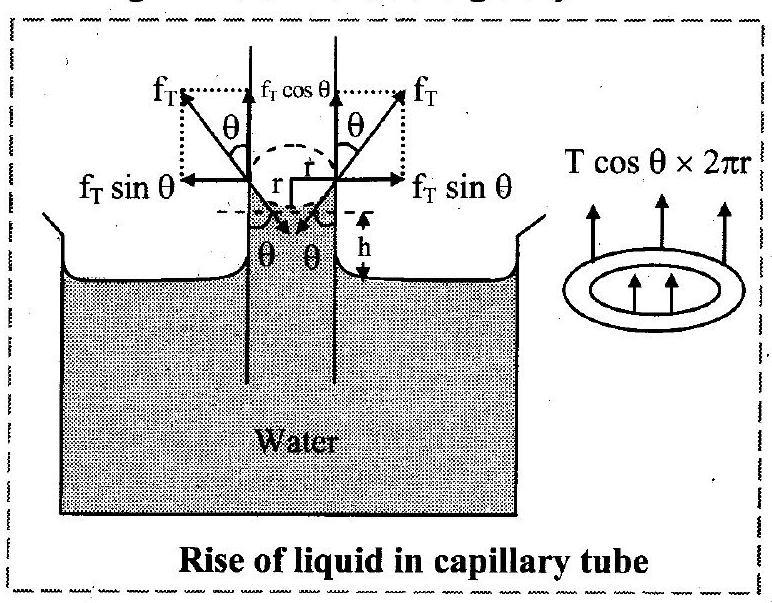
iii. The force of magnitude acts tangentially on unit length of liquid surface which is in contact with wall of capillary tube and is given as,
This force can be resolved into two components:
a. -vertically upward and
b. -along horizontal
iv. Vertical component is effective. Horizontal component is not responsible for capillary rise.
v. Vertical component of force acting on liquid column
force per unit length
circumference
vi. Upward force balances weight of liquid in the capillary.
where, volume of liquid rise in the tube (ignoring the liquid in the concave meniscus.)
mass of the liquid in the capillary rise.
This must be equal and opposite to the vertical component of the force due to surface tension.
vii. If liquid in meniscus is neglected, then for equilibrium.,
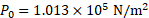
This is the required expression for rise of liquid in capillary tube
12. On the basis of molecular theory explain the phenomenon of surface tension.
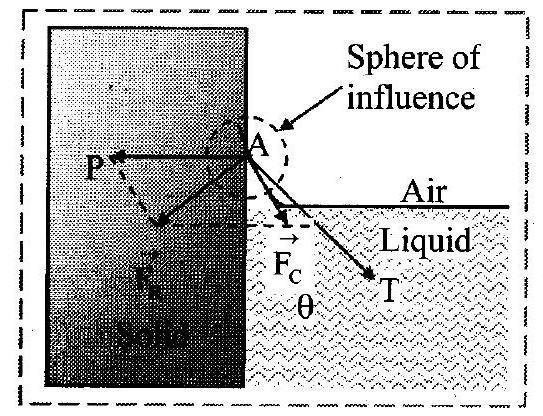
Ans: Molecular theory of surface tension:
i. Let Surface film of liquid in a container containing liquid.
PS is the free surface of liquid and QR is the inner layer parallel to PS at distance equal to the range of molecular force.
ii. Now consider three molecules A, B and C in a liquid in a vessel such that the molecule is well inside the liquid, the molecule
within surface film and molecule
is on the surface of liquid as shown in the figure.
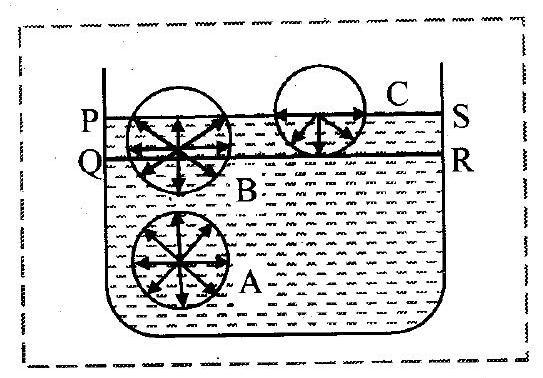
iii. The sphere of influence of the molecule is entirely inside the liquid. As a result, molecule
is acted upon by equal cohesive forces in all directions. Thus, the net cohesive force acting on molecule
is zero.
iv. For molecule B, a large part of its sphere of influence is inside the liquid and a smaller part is outside the surface (in air). The adhesive force acting on molecule due to air molecules above it and within its sphere of influence is weak compared to the strong downward cohesive force acting on the molecule. As a result, the molecule
gets attracted inside the liquid.
v. For molecule C, half of the sphere of influence is in air and half is in liquid. As density of air is much less than that of liquid, number of air molecules within the sphere of influence of the molecule above the free surface of the liquid is much less than the numbers of liquid molecules within the sphere of influence that lies within the liquid. Thus, the adhesive force due to the air, molecules acting on molecule
is weak compared to the cohesive force acting on the molecule. As a result, the molecule
also gets attracted inside the liquid. vi. Thus, all molecules in the surface film are acted upon by an unbalanced net cohesive force directed into the liquid. Therefore, the molecules in the surface film are pulled inside the liquid. This minimizes the total number of molecules in the surface film. As a result, the surface film remains under tension. The surface film of a liquid behaves like a stretched elastic membrane. This tension is known as surface tension and the force due to it acts tangential to the free surface of a liquid.
13. What is capillarity? State any two uses of capillarity.
OR
What is capillarity? Give any ‘two’ applications of capillarity.
Ans: Capillary action or capillarity:
The phenomenon of rise or fall of liquid level inside a capillary tube when it is dipped in the liquid is called capillary action or capillarity.
Uses of capillarity:
i. Oil rises up the wick of a lamp.
ii. Cloth rag sucks water.
iii. Water rises up the crevices in rocks.
iv. Sap and water rise up to the top most leaves in a tree.
v. Blotting paper absorbs ink.
[Any two uses]
- Critical velocity and Reynold’s number
1. State the formula for critical velocity in terms of Reynold’s number for a flow of a fluid.
Ans:
Formula for critical velocity is given as,
,
where, critical velocity of the fluid
Reynolds number
coefficient of viscosity
density of fluid
diameter of tube
2. Define coefficient of viscosity. State its formula and S.I. units.
Ans:
i. Coefficient of viscosity: The coefficient of viscosity is defined as the viscous force per unit area per unit velocity gradient.
ii. Formula:
iii. Unit of is
or decapoise in SI system
2.7 Stoke’s Law
1. Derive an expression for terminal velocity of a spherical object falling under gravity through a viscous medium.
Ans:
Expression for terminal velocity:
i. Consider a sphere of radius (r) and density ( ) falling under gravity through a liquid of density
and coefficient of viscosity
as shown in figure.

ii. Forces acting on the sphere during downward motion are,
a. Viscous force (directed upwards)
b. Weight of the sphere,
(directed downwards)
c. Upward thrust as Buoyant force
(directed upwards)
iii. As the downward velocity increases, the viscous force increases. A stage is reached, when sphere attains terminal velocity.
iv. When the sphere attains the terminal velocity, the total downward force acting on the sphere is balanced by the total upward force acting on the sphere.
Total downward force
Total upward force
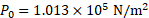
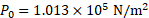
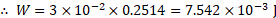
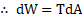
This is the expression for terminal velocity of the sphere.
Numericals
- Surface tension
1. Calculate the work done when a spherical drop of mercury of radius , falls from some height and breaks into a million droplets, each of the same size. The surface tension of mercury is
.
Solution:
Given:
To find: Work done (W)
Formula:
Calculation: Volume of a single drop and
Volume of a single droplet
We have,
or
From formula,
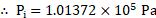
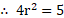
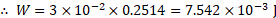
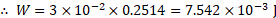
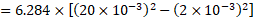
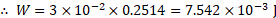
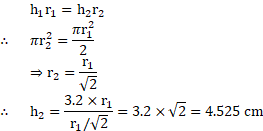
Ans: The work done when a spherical drop of mercury falls from some height and breaks into a million droplets is .
2. A soap bubble of radius is blown. Surface tension of soap solution is
. Calculate the work done in blowing the soap bubble.
Solution:
Given: dyne
To find: Work (W)
Formula:
Calculation: Initial surface area of soap bubble
Final surface area
Increase in surface area
From formula,
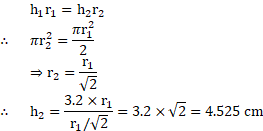
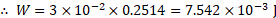
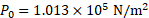
Ans: The work done in blowing the soap bubble is .
3. Calculate the density of paraffin oil, if a glass capillary of diameter dipped in paraffin oil of the surface tension
rises to a height of
. [Angle of contact of paraffin oil with glass is
and
]
Solution:
Given:
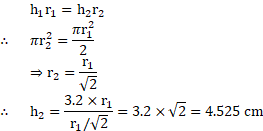
To find: Density
Formula:
Calculation: From formula,
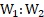
Ans: The density of paraffin oil is .
4. Water rises to a height in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
Solution:
Given:
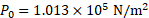
To find: Height to which water will rise
Formula:
Calculation: From formula,
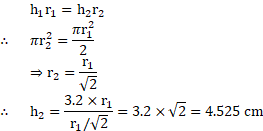
Ans: Water will rise to a height of .
5. A raindrop of diameter is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water
, atmospheric pressure
Solution:
Given:
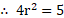
,
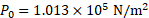
To find: Pressure inside the raindrop
Formula:
Calculation: From formula,
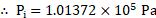
Ans: The pressure inside the raindrop is .
6. The energy of the free surface of a liquid drop is times the surface tension of the liquid. Find the diameter of the drop in C.G.S. system.
Solution:
Given:
To find: Diameter of the drop (d) in C.G.S. system
Formula:
Calculation:
From formula,
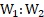
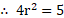
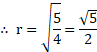
Ans: The diameter of the drop is .
7. The total free surface energy of a liquid drop is times the surface tension of the liquid. Calculate the diameter of the drop in S.I. unit.
Solution:
Given:
To find: Diameter of drop (d)
Formula:
Calculation:
From formula,
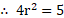
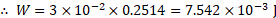
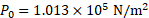
Ans: The diameter of the drop is .
8. The total energy of free surface of a liquid drop is times the surface tension of the liquid. What is the diameter of the drop?
Solution:
(Assume all terms in SI unit).
[Mar 17]
Given:
To find: Diameter of drop (d)
Formula:
Calculation: From formula,
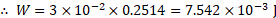
Ans: The diameter of the drop is .
9. Two soap bubbles have radii in the ratio 4:3 What is the ratio of work done to blow these bubbles?
Solution:
Given:
To find:
Formulae:
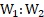
Calculation:
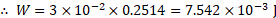
From formula,
Work done to blow both bubbles,
and
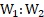
Ame: The ratio of work done to blow the bubbles is .
10. Calculate the work done in increasing the radius of a soap bubble in air from to
. The surface tension of soap solution is 30 dyne
Solution:
Given:
To find: Work (W)
Formula:
Calculation:
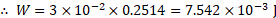
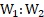
Since soap bubble has two surfaces
From formula,
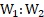
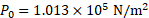
Ans: The work done in increasing the radius of the soap bubble is .
11. A horizontal circular loop of a wire of radius is lowered into crude oil and a film is formed. The force due to the surface tension of the liquid is
. Calculate the surface
Solution:
tension of the crude oil.
[July 18]
Given:
To find: Surface tension (T)
Formula:
Calculation: As there are two sides of a circular loop acted upon by the force, .
From formula,
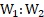
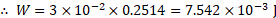
Ans: The surface tension of crude oil is .
12. A rod of length is movable on a rectangular frame of wire. A film is formed in the frame.
force of
is applied to the rod for its equilibrium. Find the surface tension of the liquid.
Solution:
Given:
To find: Surface tension (T)
Formula:
Calculation: In case of rod, liquid wets it from two sides.
Force acting on the rod due to surface tension,
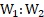
From formula,
Ans: The surface tension of the liquid is .
13. Calculate the work done in blowing a soap bubble of radius . (Surface tension of soap solution
)
Solution:
Given:
,
Initial radius of bubble ,
Final radius of bubble,
To find: Work down (W)
Formula: Work done
Calculation:
Initial surface area of bubble
A soap bubble has two surfaces, outer surface and inner surface.
Final surface area of soap bubble is,
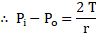
change in area
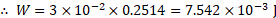
From formula,
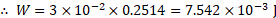
Ans: Work done in blowing a soap bubble to a radius of is
.
14. Eight droplets of water each of radius coalesce into a single drop. Find the decrease in the surface area.
Solution:
Given: ,
To find: Decrease in surface area (E)
Formula:
Calculation: Volume of a single drop and
Volume of a single droplet
We have,
or
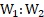
From formula,
Ans: Decrease in the surface area is .
15. Find the difference of pressure between inside and outside of a spherical water drop of radius , if surface tension of water is
.
Solution:
Given:
To find: Difference of pressure
Formula:
Calculation: From formula,
Ans: The difference of pressure between inside and outside of a spherical water drop is .
16. Calculate the work done in blowing a soap bubble to a radius of . The surface tension of soap solution is
.
Solution:
Given: ,
Initial radius of bubble , Final radius of bubble,
To find: Work down (W)
Formula: Work done
Calculation: Initial surface area of bubble
A soap bubble has two surfaces, outer surface and inner surface.
Final surface area of soap bubble is,
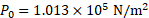
change in area
From formula,
Ans: Work done in blowing a soap bubble to a radius of is
.