07 Wave Optics
Multiple Choice Questions
1. Huygens’ Wave Theory of light could not explain……………………
(A) reflection
(B) refraction
(C) interference
(D) Photoelectric effect
Ans. (D) Photoelectric effect
2. In interference of light, a point is bright if the path difference between the two beams arriving at that point is……………………
(A) an integral multiple of the wavelength
(B) an odd multiple of the wavelength
(C) an odd multiple of half of the wavelength
(D) an even multiple of the wavelength
Ans. (D) an even multiple of the wavelength
3. In the biprism experiment keeping the experimental set up unchanged, the fringe width ……………………
(A) increases with increase in wavelength.
(B) decreases with increase in wavelength.
(C) increases with decrease in wavelength.
(D) remains unchanged with change in wavelength.
Ans. (A) increases with increase in wavelength.
4. A parallel beam of light traveling in glass is incident obliquely on water surface. After refraction, its width……………………
(A) decreases
(B) increases
(C) remains same
(D) becomes zero
Ans. (B) increases
5. For destructive interference, the phase difference between two waves should be
(A) , ……………………
(B) , ……………………
(C) , ……………………
(D) , ……………………
Ans. (C) , ……………………
6. In the diffraction pattern due to a single slit of width ‘ ‘ with incident light of wavelength ‘
‘, at an angle of diffraction ‘
‘, the condition for first minimum is……………………
(A)
(C)
(B)
(D)
Ans. (B)
7. The fringes produced in diffraction pattern are of……………………
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity
(D) equal width with varying intensity
Ans. (B) unequal width with varying intensity
8. A ray of light passes from vacuum to a medium of refractive index . Angle of incidence is found to be twice the angle of refraction. The angle of incidence is given by
(A)
(B)
(C)
(D)
Ans. (C)
9. The resolving power of telescope of aperture for light of wavelength
is……………………
(A)
(B)
(C)
(D)
Ans. (A)
10. If numerical aperture of a microscope is increased, then its……………………
(A) resolving power decreases.
(B) limit of resolution decreases.
(C) resolving power remains constant.
(D) limit of resolution increases.
Ans. (B) limit of resolution decreases.
11. The numerical aperture of objective of a microscope is 0.12 . The limit of resolution, when light of wavelength is used to view an object is
(A)
(B)
(C)
(D)
Ans. (C)
12. Light of a certain wavelength has a wave number in vacuum. Its wave number in a medium of refractive index
is……………………
(A)
(B)
(C)
(D)
Ans. (D)
13. If the polarizing angle for a given medium is , then the refractive index of the medium is
(A)
(B) 1
(C)
(D)
Ans. (D)
14. The resolving power of a telescope depends upon the……………………
(A) length of the telescope
(B) focal length of an objective
(C) diameter of an objective
(D) focal length of an eyepiece
Ans. (C) diameter of an objective
15. A parallel beam of light travelling in water is incident obliquely on a glass surface. After refraction its width……………………
(A) decreases
(B) increases
(C) remains the same
(D) becomes zero
Ans. (B) increases
16. If ‘ ‘ is the aperture of telescope and ‘
‘ is the wavelength of light then resolving power of telescope is……………………
(A)
(B)
(C)
(D)
Ans. (D)
17. Using monochromatic light of wavelength in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of……………………
(A)
(B)
(C)
(D)
Ans. (D)
18. In interference pattern, using two coherent sources of light; the fringe width is……………………
(A) directly proportional to wavelength
(B) inversely proportional to square of the wavelength.
(C) inversely proportional to wavelength.
(D) directly proportional to square of the wavelength.
Ans. (A) directly proportional to wavelength
19. Glass plate of refractive index 1.732 is to be used as a polariser, its polarising angle is……………………
(A)
(B)
(C)
(D)
Ans. (C)
20. The condition for destructive interference between two waves is that their phase difference should be……………………
(A)
(B) .
(C)
(D)
Ans. (C)
21. When a ray of light enters into water from air, ……………………
(A) its wavelength decreases
(B) its wavelength increases
(C) its frequency increases
(D) its frequency decreases
Ans. (A) its wavelength decreases
22. A diffraction pattern is obtained by making blue light incident on a narrow slit. If blue light is replaced by red light, then the diffraction bands……………………
(A) disappear
(B) become broader
(C) become narrower
(D) remain same
Ans. (B) become broader
23. In Young’s double slit experiment the two coherent sources have different amplitudes. If the ratio of maximum intensity to minimum intensity is , then the ratio of amplitudes of the two source will be……………………
(A)
(B)
(C)
(D)
Ans. (B)
24. What changes are observed in a diffraction pattern if the whole apparatus is immersed in water?
(A) the wavelength of light increases
(B) width of central maximum increases
(C) width of central maximum decreases
(D) frequency of light decreases
Ans. (C) width of central maximum decreases
25. The property of light which remains unchanged when it travels from one medium to another is……………………
(A) velocity
(C) amplitude
(B) wavelength
(D) frequency
Ans. (D) frequency
Theory Questions
7.4 Huygens’ Theory
- State Huygens’ principle.
Ans: Statement: Each point on a wavefront acts as a secondary source of light emitting secondary light waves called wavelets in all directions which travel with the speed of light in the medium. The new wavefront can be obtained by taking the envelope of these secondary wavelets travelling in the forward direction and is thus, the envelope of the secondary wavelets in forward direction. The wavelets travelling in the backward direction are ineffective.
2. Explain the construction of plane wavefront using Huygens’ principle.
Ans:
i. A plane wavefront is formed when point of observation is very far away from the primary source.
ii. Let represent a plane wavefront at any instant. According to Huygens’ principle, all the points on this wavefront will act as secondary sources of light sending out secondary wavelets in the forward direction as backward travelling wavelets are supposed to be ineffective.
iii. Draw hemispheres with .. as centres and ‘
‘ as radius. The surface tangential to all such hemispheres is
at instant ‘
‘. It is a new wavefront at time ‘
‘.
iv. The plane wavefronts are propagated as plane waves in medium. They are parallel to each other.
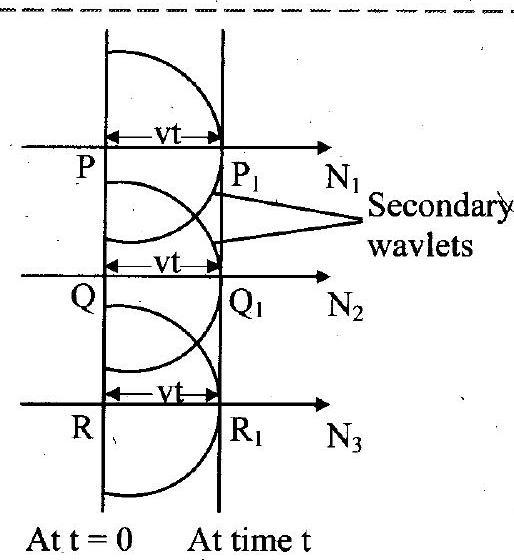
PQR: Plane wavefront at any instant, : Plane wavefront after time ‘
‘
v. show the direction of propagation of plane wavefront.
vi. The new wavefront is parallel to primary wavefront
.
7.5 Reflection of Light at a Plane Surface
- Derive the laws of reflection of light using Huygens’ principle.
OR
With the help of a neat diagram, explain the reflection of light on a plane reflecting surface.
Ans: Reflection of light on a plane surface:
i. A plane wavefront is advancing obliquely towards plane reflecting surface
with velocity ‘
‘.
and
are incident rays.
ii. When ‘ ‘ reaches
at
, then ray at ‘
‘ reaches point ‘
‘ and it has to cover distance
to reach the reflecting surface
.
iii. Let ‘ ‘ be the time required to cover distance
. During this time interval, secondary wavelets are emitted from
and will spread over
hemisphere of radius
, in the same medium.
Distance covered by secondary wavelets to reach from to
in time
is same as the distance covered by primary waves to reach from
to
.
Thus .
iv. All other rays between and
will reach
after
and before
. Hence, they will also emit secondary wavelets of decreasing radii.
v. The surface touching all such hemispheres is which is reflected wavefront, bounded by reflected rays
and
.
vi. Draw and
.
Thus, angle of incidence is
and angle of reflection is
.
and
vii. In and
(Reflected waves travel equal distance in same medium in équal time).
…(common side)
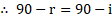
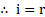
viii. Also, from the figure, it is clear that incident ray, reflected ray and normal lie in the same plane.
ix. This explains reflection of light from plane reflecting surface on the basis of Huygens’ principle.
7.6 Refraction of Light at a Plane Boundary Between Two Media
- Explain refraction of a plane wavefront at a plane surface on the basis of Huygens’ wave theory of light.
Ans:
Explanation:
i. Let be the plane refracting surface separating two media air and glass of refractive indices
and
respectively.
ii. A plane wavefront is advancing obliquely towards
from air. It is bounded by rays
and
which are incident rays.
iii. When ‘ ‘ reaches ‘
‘, then ‘
‘ will be at ‘
‘. It still has to cover distance
to reach
.
iv. According to Huygens’ principle, secondary wavelets will originate from and will spread over a hemisphere in glass.
v. All the rays between and
will reach
and spread over the hemispheres of decreasing radii in glass. The surface of tangency of all such hemispheres is
. This gives rise to refracted wavefront
in glass. vi.
and
are refracted rays.
vii. Let and
be the velocities of light in air and glass respectively.
viii. At any instant of time ‘ ‘, distance covered by incident wavefront from
to
Distance covered by secondary wave from to
.
Proof of laws of refraction:
i. From figure,
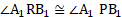
and
From equations (1) and (2),
ii. Similarly,
We have,
and
From equations (3) and (4),
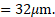
iii. In
iv. In
v. Dividing equation (5) by (6),
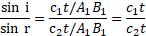
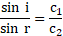
Also
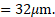
vi. From the explanation, it is clear that incident rays , refracted rays
and normal
and
lie on the same plane
. Also, incident ray
and refracted ray
lie on opposite sides of normal MN. Hence, laws of refraction can be explained.
- On the basis of Huygens’ wave theory of light, prove that velocity of light in a rarer medium is greater that velocity of light in a denser mediùm.
Ans: Refer Subtopic 7.6: Q. No 1 [(i) to (v)]
vi. From figure,
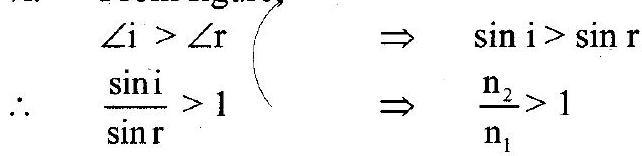
vii. Since,
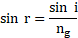
Hence, velocity of light in rarer medium is greater than velocity in denser medium.
- Explain refraction of light on the basis of wave theory. Hence prove the laws of refraction.
Ans: Refer Subtopic 7.6: Q. No. 1.
7.7 Polarization
- What is polariszaion of light ? State and explain Brewster’s law.
Ans: The phenomenon of restriction of the vibration of light waves in a particular plane perpendicular to direction of wave motion is called polarization of light.
Statement: The tangent of the polarizing angle is equal to the refractive index of the refracting medium at which partial reflection takes place.
According to Brewster’s law,
where, and
are refractive indices of two media.
Explanation of Brewster law:
i. When light is incident at an angle on a boundary between two transparent media having refractive indices and
, part of it gets refracted and the rest gets reflected.
ii. Consider unpolarized light incident from rarer medium of refractive index on such a boundary that is perpendicular to the plane of the paper, as shown below,
iii. For a particular angle of incidence (shown in the figure), the reflected wave is completely plane polarized with its electric field perpendicular to the plane of the paper while the refracted wave is partially polarized. This particular angle of incidence is called the Brewster’s angle
.
iv. For this angle of incidence, the refracted and reflected rays are perpendicular to each other. For angle of refraction
,
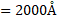
From laws of refraction,
Using (1)]
,
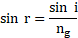
This is the expression for Brewster’s angle.
- Draw a neat labelled diagram showing the plane of vibration and plane of polarisation for polarised light.
Ans:
- What is a polaroid? State its ‘two’ uses.
Ans: polaroid is a kind of synthetic plastic sheet which is used as polarizer.
Uses of Polaroids:
i. Polaroids are used to produce and analyse polarised light.
ii. Sunglasses are fitted with polaroid which reduce the intensity of the partially or fully polarized reflected light coming to the eyes from reflecting surfaces.
- State Brewster’s law and show that when light is incident at polarizing angle, the reflected and refracted rays are mutually perpendicular to each other.
Ans: Refer Subtopic 7.7 : Q. No. 1 (Statement only)
i. In the figure,
incident ray,
refracted ray,
reflected ray
ii. From Snell’s law,
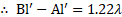
From Brewster’s law,
iii. From equations (1) and (2),
iv. In the figure,
….(From laws of reflection)
But
…[From equation (3)]
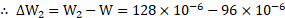
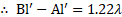
Hence reflected and refracted rays are perpendicular at polarising angle.
7.8 Interference
- What is interference of light?
Ans: Interference of light is defined as the modification in the intensity of light (larger at some places and smaller at some places) produced by the superposition of two or more light waves.
- State the conditions necessary for obtaining sharp and steady interference pattern.
Ans: Conditions for obtaining sharp and steady interference pattern are:
i. The two sources of light must be coherent.
ii. The two sources of light must be monochromatic. iii. The two interfering waves must have the same amplitude.
iv. The separation between the two slits (d) must be small in comparison to the distance between the plane containing the slits and the observing screen (D).
v. The two slits should be narrow.
vi. The two waves should be in the same state of polarization if polarized light is used for the experiment.
- Using analytical method for interference bands, obtain an expression for path difference between two light waves. [July 16]
Ans:
i. Let and
be the two coherent monochromatic sources which are separated by short distance
. They emit light waves of wavelength
.
ii. Let horizontal distance between screen and source.
iii. Draw and
perpendicular bisector of slit.
Since , the path difference between waves reaching
from
and
is zero, therefore there is a bright point at
.
iv. Consider a point on the screen which is at a distance
from the central point
on the screen. Light waves from
and
reach at
simultaneously by covering path
and
, where they superimpose.

Derivation:
In
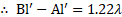
In
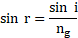
Subtract equation (1) from (2),
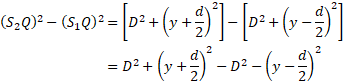
Equation (4) gives the path difference of two interfering light waves.
- Obtain an expression for path difference and fringe width of interference pattern in Young’s double slit experiment. Show that the fringe width is same for consecutive bright and dark bands.
Ans: Refer Subtopic 7.8: Q. No. 3. for the expression of path difference.
Point will be bright if,
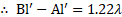
where .
….[From equation (4)].
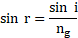
Equation (5) represents distance of bright fringe from central bright fringe.
Point will be dark point if,
where .
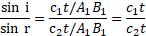
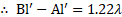
Equation (6) represents distance of dark fringe from central maximum.
Fringe width:
The distance between any two successive dark or any two successive bright fringes is equal. This is called the fringe width and is given by, Fringe width
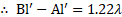
Thus, both dark and bright fringes are equidistant and have equal widths.
- State the conditions to get constructive and destructive interference of light. [Mar 18]
Ans: Conditions to get constructive interference:
i. Two waves should be in same phase.
ii. The phase difference between the interfering waves should be even multiple of .
.
, where,
iii. The path difference between the interfering waves should be an integral multiple of or even multiple of
.
i.e.,
where, .
Conditions to get destructive interference:
i. Two waves should be in opposite phase.
ii. The phase difference between the interfering waves should be odd multiple of .
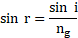
, where,
iii. The path difference between the interfering waves should be odd multiple of .
i.e., .
where,
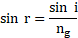
Thus, constructive interference is obtained when path difference is an odd multiple of half wavelength.
- Giye the ànalytical treatment for interference bands. Hence obtain an expression for path difference between the interfering waves.
Ans: Refer Subtopic 7.8: Q. No. 3.
7.9 Diffraction of Light
- . What is ‘diffraction of light’? Explain its two types.
Ans: The bending of light near the edge of an obstacle or slit and spreading into the region of geometrical shadow is called diffraction of light.
Two types of diffraction are:
i. Fraunhofer diffraction:
a. If the distances between the primary source of light, the obstacle/slit causing diffraction and the screen for viewing the diffraction pattern are very large, the diffraction is called Fraunhofer diffraction.
b. In this case, the wavefront incident on the obstacle can be considered to be a plane wavefront.
ii. Fresnel diffraction: In this case, the distances are much smaller and the incident wavefront is either cylindrical or spherical depending on the source.
- Distinguish between the phenomenon of interference ạnd diffraction of light.
Ans: Difference between interference and diffraction:
| i. | Interference is due tosuperposition of wavesfrom differentwavefronts. | Diffraction is due tomany waves comingfrom different parts ofthe same wavefront. |
| ii. | All bright fringes areof equal intensity. | Intensity decreaseswith the order ofbright band. |
| iii. | Minimum intensitymay be zero. | Minimum intensity isnot zero. |
| iv. | Width of the centralmaximum is same asthat of other brightfringes i.e fringe widthis same for all fringesincluding centralmaxima. | Width of centralmaximum is broaderthan other maximaand it is double thefringe width. |
| v. | The waves emitted bytwo coherent sourcestravel in straight line. | The light waves arebent at the cornersand displaced fromtheir straight linepath. |
| vi. | The resolving power ofan optical instrumentdoes not depend on thephenomenon ofinterference. | The resolving powerof an opticalinstrument dependson the phenomenon ofdiffraction. |
- What happens to the fringe width in diffraction pattern if the diameter of wire is increased?
[July 22]
Ans: If the diameter of wire is increased, the fringe width in diffraction pattern decreases.
7.10 – Resolving Power
- Explain the resolving power of a telescope with the help of a neat ray diagram. On what factors does it depend?
Ans:
i. Telescope is used to see distant stars which can be considered to be luminous point objects. Hence, their diffraction patterns are Airy discs.
ii. Also, as the objects to be seen are far off, only the angular separation between the two is of importance and not the linear separation between them
iii. Consider of a telescope receiving two sets of parallel beams from two distant objects with an angular separation
, as shown in figure below:

iv. According to Rayleigh’s criterion, the minimum separation between the images I and I’ must be equal to the radius of the first dark Airy ring.
v. If Airy’s theory is applied to Fraunhofer diffraction of a pair of point objects, the path difference between the extreme rays, at the first dark ring is given by .
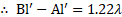
vi. If is the aperture of the telescope (diameter
of its objective),
and
resolving power,
vii. Factors: Resolving power of telescope depends upon the aperture of lens of the objective of telescope and wavelength of light used.
- What is resolving power of an optical instrument?
Ans: Ability to distinguish two physically separated objects as two distinct objects is known as the resolving power of an optical instrument.
- Explain Rayleigh’s criterion for the resolution of two close point objects, when their images are
i. just resolved, ii. well resolved and
iii. unresolved.
OR
Explain Rayleigh’s criterion for central maximum.
Ans:
i. According to Lord Rayleigh, the ability of an optical instrument to distinguish between two
closely spaced objects depends upon the diffraction patterns of the two objects (slits, point objects, stars, etc.), produced at the screen (retina, eyepiece, etc.).
ii. The two objects are said to be unresolved, if the separation between the central maximum of the two object is less than the distance between the central maximum and first minimum of any of the two objects i.e.,
iii. Two objects are said to be just resolved when the separation between the central maxima of the two objects is just equal to the distance between the central maximum and the first minimum of any of the two objects i.e., .
iv. The two objects are said to be well resolved, if the separation between the central maximum of the two objects is greater than the distance between the central maximum and first minimum of any of the two objects i.e., .

v. Thus, depression in the resultant envelope is not noticeable in : unresolved diffraction pattern, noticeable in just resolve diffraction pattern and clearly noticeable in well resolved pattern.
- State the factors on which resolving power of microscope depends. How can it be increased?
Ans:
i. Resolving power of microscope depends on numerical aperture of objective of microscope and wavelength of light used.
ii. Resolving power of a microscope can be increased by,
a. Reducing distance of separation between two objects,
b. Eyepiece should be filled with material of high refractive index (n) such as oil,
c. Source with small value of wavelength should be used.
Numericals
7.6. Refraction of Light at a Plane Boundary Between Two Media
- Determine the change in wavelength of light during its passage from air to glass, if refractive index of glass with respect to air is 1.5 and frequency of light is
. [Velocity of light in air
].
Find the wave number of light in glass.
Solution:
Given:
To find: i. Change in wavelength of light
ii. Wave number of light .
Formulae: i. ii.
iii.
Calculation: i. Using formula (iii),
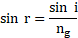
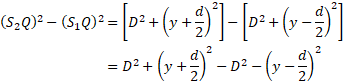
Ans: i. Change in wavelength of light is . ii. Wave number of light is
.
- A ray of light is incident on a water surface of refractive index
making an angle of
with the surface. Find the angle of refraction.
Solution:
Given:
To find: Angle of refraction (r)
Formula:
Calculation: Using formula,
Ans: Angle of refraction is .
- The refractive indices of water for red and violet colours are 1.325 and 1.334 respectively. Find the difference between velocities of the rays for these two colours in water.
Solution:
Given:
To find: Difference between velocities
Formula:
Calculation: From formula,
Ans: The difference between the velocities of rays for red and violet colours in water is .
- If’the difference in velocities of light in glass and water is
, find the velocity of light in air.
Refractive index of glass
, Refractive index of water
Solution:
Given:
To find: Velocity of light in air (c)
Formula:
Calculation: From formula,
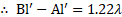
Ans: The velocity of light in air is .
- Red light of wavelength
in air has wavelength
in glass. If the wavelength of violet light
Solution:
in air is , find its wavelength in glass. (Assume that
)
[Oct 14]
Given:
To find: Wavelength
Formula:
Calculation: From formula,
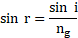
Ans: The wavelength of violet light in glass is .
- A parallel beam of monochromatic light is incident on glass slab at an angle of incidence
. Find the ratio of the widths of the beam in glass to that in air, if refractive index of glass is 1.5 .
Solution:
Given:
,
Let width of beam in glass slab,
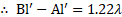
To find: Ratio of widths
Formulae: i.
ii.
Calculation: From formula (i),
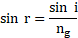
Ratio of the widths of beam
Ans: The ratio of widths of the beam in glass to that in air is .
- Determine the change in wavelength of light during its passage from air to glass. If the refractive index of glass with respect to air is 1.5 and the frequency of light is
, find the wave number of light in glass. [Velocity of light in air
]
Solution:
Given:
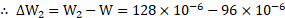
To find: i. Change in wavelength of light ii. Wave number of light
Formulae:
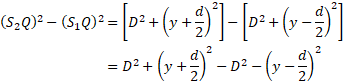
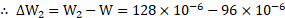
Calculation: i. : Using formula (iii),
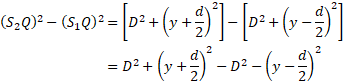
Ans: i. The change in wavelength of light is . ii. The wave number of light is
.
- Determine the change in wavelength of light during its passage from air to glass, if the refractive index of glass with respect to air is 1.5 and the frequency of light is
. Find the wave number of light in glass (velocity of light in air
).
Solution:
Given:
To find: i.
Change in wavelength
ii. Wave number of light in glass
Formulae:
i.
ii.
iii.
Calculation: i. Using formula (iii),
From formula (i),
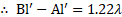
Change in wavelength
ii. From formula (ii),
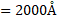
Wave number of light in glass
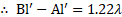
Ans: i. Change in wavelength of light is
ii. Wave number of light in glass is
- The width of plane incident wavefront is found to be doubled on refraction in denser medium. If it makes an angle of
with the normal, calculate the refractive index for the denser medium.
Solution:
Given: , Let
be width of incident wavefront and
be width of refracted wavefront.
To find: Refractive index (n)
Formulae: i.
ii.
Calculation: From formula (i),
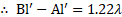
Ans: The refractive index for the denser medium is 1.697.
- The refractive indices of glass and water w.r.t. air are
and
respectively. Determine the refractive index of glass w.r.t. water.
Solution:
Given:
To find: Refractive index of glass w.r.t. water
Formula:
Calculation: From formula,
An: The refractive index of glass w.r.t. water is 1.12.
- The refractive indices of water and diamond are
and 2.42 respectively. Find the speed of light in water and diamond.
Solution:
Given:
To find: i. speed of light in water ii. speed of light in diamond
Formula:
Calculation: Using formula,
For water,
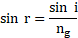
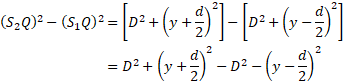
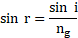
For diamond,
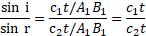
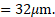
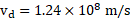
Ans: i. Speed of light in water is . ii. Speed of light in diamond is
.
- A parallel beam of monochromatic light is incident on a glass slab at an angle of incidence
, gets refracted through an angle of
. Find the ratio of width of parallel beam in air to that in glass.
Solution:
Given:
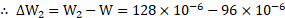
Let width of beam in glass slab,
width of beam in air
To find: Ratio of widths
Formula:
Calculation: From formula,
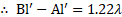
Ans: The ratio of widths of the beam in glass to that in air is .
- If the difference in the velocities of light in glass and water is
, calculate the velocity of light in air. Given that refractive index of glass and water with respect to air are 1.5 and
respectively.
Solution:
Given:
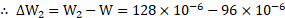
To find: Velocity of light in air
Formulae: i.
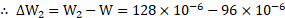
Calculation: From formula (i) and (ii),
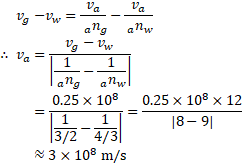
Ans: The velocity of light in air is .
7.7 Polarization
- For a glass plate as a polariser with refractive index 1.633 , calculate the angle of incidence at which light is polarised.
Solution:
Given:
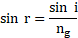
To find: Polarising angle
Formula:
Calculation: From formula we get,
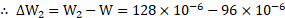
Ans: The angle of incidence at which light is polarised is ,
- Find the polarising angle for the material of refractive index
.
Solution:
Given:
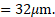
To find: Polarising angle
Formula:
Calculation: From formula we get,
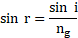
Ans: The angle of incidence at which light is polarised is .
7.8 Interference
- In a biprism experiment the slit is illuminated by a light of wavelength 4800 A.U. The distance between slit and biprism is
and the distance between biprism and eye piece is
. If the distance between virtual sources is
, determine the distance between the
bright band on side of the central band and
dark band on other side.
Solution:
Given:
To find: Distance between
bright band on one side and
dark band on the other side of the central bright band,
Formulae: i. For bright band,
ii. For
dark band,
Calculation: From formula (i),
From formula (ii),
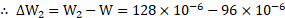
Ans: The distance between bright band on one side and
dark band on the other side of the central bright band is
.
- In Young’s experiment, two slits separated by
are illuminated by a light of wavelength 6400 A.U. Interference fringes are obtained at a distance of
from the slits. Find the changes in the fringe width, if the separation between the slits is –
i. increased by, and
ii. decreased by.
Solution:
Given:
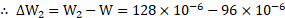
To find: Changes in fringe width
Formula:
Calculation: From formula,
Also, .
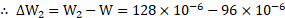
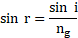
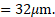
Ans: Changes in fringe width respectively are and
.
- A point is situated at
and
from two coherent sources. Find the nature of illumination at the point if wavelength of light is
.
Solution:
Given:
To find: Nature of illumination
Formula:
Calculation: Nature of illumination is determined by path difference.
Path difference,
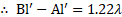
Now,
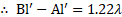
Since the path difference is even multiple of ,
Point is bright.
Ans: The nature of illumination of point is bright.
- In a biprism experiment, a slit is illuminated by a light of wavelength
. The distance between the slit and biprism is
and the distance between the biprism and eyepiece is
. If the distance between virtual sources is
, determine the distance between
bright band on one side and
dark band on the other side of the central bright band.
Solution:
Given:
To find: Distance between
bright band on one side and
dark band on the other side of the central bright band,
Formulae: i. For bright band,
ii. For dark band,
Calculation: From formula (i),
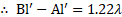
From formula (ii),
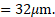
Ans: The distance between bright band on one side and
dark band on the other side of the central bright band is
.
- In a biprism experiment, when a convex lens was placed between the biprism and eyepiece at a distance of
from the slit, the virtual images of the slits are found to be separated by
. If the distance between the slit and biprism is
and between the biprism and eyepiece is
, find the linear magnification of the image.
Solution:
Given:
To find: Linear magnification
Formula:
Calculation: From formula,
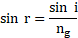
Ans: The linear magnification of the image is 2.
- In biprism experiment,
dark band is observed at
from the central bright point on the screen with red light of wavelength
. By how much will fringe width change if blue light of
Solution:
wavelength
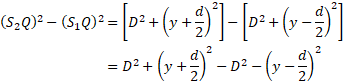
is used with the same setting?
[Mar 16]
Given:
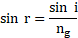
To find: Change in fringe width
Formulae: i.
ii.
Calculation: Using formula (ii),
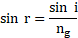
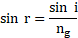
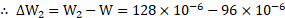
From formula (i) we can conclude, for same setting,
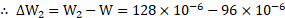
i.e.,
Change in fringe width
Ans: The change in fringe width is .
- A point is situated at
and
from two coherent sources. Find the nature of illumination at the point if wavelength of light is
.
Solution:
Given: ,
To find: Nature of illumination at the point
Formula:
Calculation: Path difference is given by,
From formula;
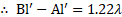
As the path difference is even multiple of , the point is bright.
Ans: The point is bright.
- The optical path difference between two identical waves arriving at a point is
. Is the point bright or dark? If the path difference is
, calculate the wavelength of light used.
Solution:
Given: Optical Path difference
Path difference
To find: Whether the point is bright or dark,
Wavelength of light used
Calculation: Path difference,
Since path difference is even multiple of , point is a bright point
Also, Path difference,
Ans: The point is bright and wavelength of light is .
- In Young’s double slit experiment, the slits are
apart and interference is observed on a screen placed at a distance of
from the slit. It is found that
bright fringe is at a distance of
from the
dark fringe, on the same side of the centre of the fringe pattern. Find the wavelength of light used.
Solution:
Given:
,
To find: Wavelength of light
Formula:
Calculation: Since distance of bright band from centre is,
Distance of dark band from centre is,
Now,
Ans: The wavelength of light is .
- In Young’s experiment interference bands were produced on a screen placed at
from two slits,
apart and illuminated by the light of wavelength
. Calculate the fringe width.
Solution:
Given: ,
To find:
Fringe width
Formula:
Calculation: From formula,
Ans: The fringe width is .
- Two coherent sources of light having intensity
produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
Solution:
To find: Ratio of intensity of maxima and minima
Formulae: i.
ii.
Calculation: From formula (i),
From formula (ii),
Ans: The ratio of intensity of maxima and minima is .
- In a biprism experiment, light of wavelength
is used to obtain an interference pattern on the screen. The fringe width changes by
when the screen is moved towards the biprism by
. Calculate the distance between the two virtual images of the slit.
Solution:
Given:
To find: . distance between two virtual images (d)
Formula:
Calculation: From formula,
Ans: The distance between the two virtual images of the slit is .
- Plane wavefront of light of wavelength
is incident on two slits on a screen perpendicular to the direction of light rays. If the total separation of 10 bright fringes on a screen
away is
, find the distance between the slits.
Solution:
Given: , Distance between 10 fringes
.
fringe width
To find: Distance between slits (d)
Formula:
Calculation: From formula,
Ans: The distance between two slits is .
- A plane wavefront of light of wavelength
is incident on two slits on a screen perpendicular to the direction of light ray. If the total separation of 10 bright fringes on a screen
away is
, find the distance between the slits.
Solution:
Given: , Distance between 10 fringes
.
Fringe width
To find: Distance between slits (d)
Formula:
Calculation: From formula,
Ans: The distance between two slits is .
- In a biprism experiment, the fringes are observed in the focal plane of the eye-piece at a distance of
from the slit. The distance between the central bright band and the 20th bright band is
. When a convex lens is placed between the biprism and the eye-piece,
from the eyepiece, the distance between the two virtual magnified images is found to be
. Determine the wavelength of light used.
Solution:
Given: ,
Magnified image,
.
To find: Wavelength
Formulae: i.
ii.
Calculation: From formula (i),
.
From formula (ii),
Ans: Wavelength of the light used is A.
7.9 Diffraction of Light
- In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is
. The screen on which the pattern is displaced, is
from the slit and wavelength of light used is
. Calculate width of the slit and width of the central maximum.
Solution:
Given:
To find: Width of slit (a)
Width of central maximum (W)
Formulae: i.
ii.
Calculation: From formula (i),
Ans: i. The width of the slit is .
ii. The width of the central maximum is .
- Monochromatic light of wavelength
falls on a slit of width ‘
‘. For what value of ‘
‘ the first maximum falls at
?
Solution:
Given:
To find:
Formula: For secondary maxima,
Calculation: From formula, for first secondary maximum,
Ans: For slit of width , the first maximum falls at
.
7.10 Resolving Power
- The minimum angular separation between two stars is
, if telescope is used to observe them with an objective of aperture
. Find the wavelength of light used.
Solution:
Given:
To find: Wavelength of light used
Formula:
Calculation: From formula,
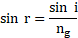
Ans: The wavelength of light used is .