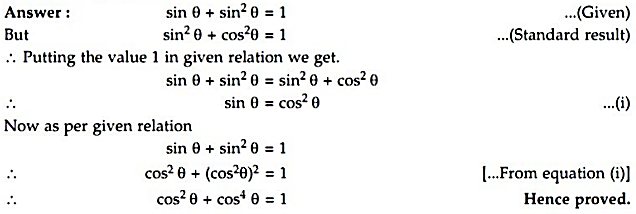2020
MATHEMATICS PART-II
General Instructions :
(i) All questions are compulsory.
(ii) Use of calculator is not allowed.
(iii) The numbers to the right of the questions indicate full marks.
(iv) In case of ‘s . No. 1(A)] only the first attempt will be evaluated and will be given credit.
(v) For every MCQ, the correct alternative or in front of sub-question number is to be written as an answer.
(vi) Draw proper figures for answers wherever necessary.
(vii) The marks of construction should be clear and distinct. Do not erase them.
(viii) Diagram is essential for writing the proof of the theorem.
1. (A) Four alternative answers are given for every sub-question. Select the correct alternative and write the alphabet of that answer :
(i) Out of the following which is the Pythagorean triplet?
(A)
(B)
(C)
(D)
Answer : (B)
(ii) Two circles of radii and respectively touch each other externally. What is the distance between their centres?
(A)
(B)
(C)
(D)
Answer : (C)
(iii) Distance of point from the origin is
(A) 7
(B) 1
(C) -5
(D) 5
Answer : (D) 5
(iv) Find the volume of a cube of side :*
(A)
(B)
(C)
(D)
Answer : Answer is not given due to the change in reduced syllabus.
(B) Solve the following questions :
(i) The ratio of corresponding sides of similar triangles is , then find the ratio of their areas.
Answer : Ratio of areas of similar triangles Ratio of corresponding sides of similar triangles)
(ii) Find the diagonal of a square whose side is .
Answer : Let is a square
(Given)
In
Diagonal of the square
(iii) is cyclic. If , then find measure of .
Answer : is cyclic

(iv) Find the slope of the line passing through the points and .
Answer : Answer is not given due to the change in reduced syllabus.
2. (A) Complete and write the following activities (Any two) :
(i) In the figure given, ‘ ‘ is the centre of the circle, seg PS is a tangent segment and is the point of contact. Line is a secant. If , find . *
Solution : Answer is not given due to the change in reduced syllabus.
(ii) If , find the value of .
Answer :
… by taking square roots
Type of arc | Name of the arc | Measure of the arc |
Minor arc | ||
Major arc |
(iii) In the figure given, is the centre of the circle. Using given information complete the following table :*

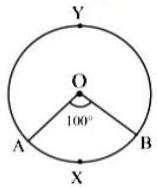
Answer : Answer is not given due to the change in reduced syllabus.
(B) Solve the following sub-questions (Any four) :
(i) In II . If , then find .
Answer : Given
(Basic proportionality theorem)..(i)
But (Given)

Equation (i) becomes,
Ans.
(ii) In , seg seg . If , then find .
Answer : In , seg seg MP
According to right-angled triangle geometric mean subtheorem

(iii) In the figure given above, is the centre of the circle and seg is a tangent segment. is a point of contact. If , then find the radius of the circle.
Answer : In given figure, radius tangent segment KL
…(Tangent theorem)
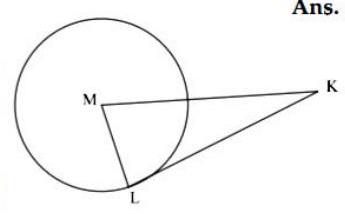
In right-angled
(iv) Find the co-ordinates of midpoint of the segment joining the points and .
Answer : Given points are and
Let,
We Know,
(v) A person is standing at a distance of 80 metres from a Church and looking at its top. The angle of elevation is of 45 . Find the height of the Church.*
Answer : Answer is not given due to the change in reduced syllabus.
3. (A) Complete and write the following activities (Any one) :
(i) In the given figure, is any point in the interior of the triangle. Point is joined to the vertices of triangle. seg PQ II seg DE, seg QR II seg EF. Complete the activity and prove that seg PR II seg DF.
Proof : In
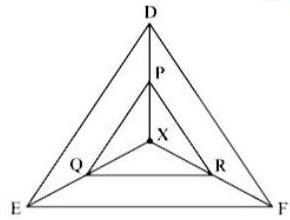
In
…(Given)

Seg PR || seg DF

…[From (i) and (ii)]
…(By converse of basic proportionality theorem) …(Given)
…(Basic proportionality theorem)
Answer : In
In
Basic proportionality theorem | |||
From (i) and (ii)] |
Seg PR||seg DF …(By converse of basic proportionality theorem)
(ii) If and are the vertices of , show that is a parallelogram.*
Answer : Answer is not given due to the change in reduced syllabus.
(B) Solve the following sub-questions (Any two) :
(i) If , point is the mid-point of side . If , find QR.
Answer : In , point is the mid-point of side .
Segment is median of
According to Apollonius’s theorem

As per given values,
We know, point is the mid-point of side
[From equation (i)]
unit
Ans.
(ii) Prove that, tangent segments drawn from an external point to the circle are congruent.
Answer : Point is the centre of the circle and point is external to the circle. Segment PA and segment PB are tangent segments to the circle. Point and point are touch points of the tangent segments.
Prove :
Construction : Draw OA, OB and OP.
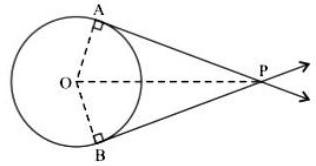
Proof : Each tangent of a circle is perpendicular to the radius drawn through the point of contact
… (Theorem)
Radius and, Radius
and
and are right-angled triangles.
Now in and ,

(iii) Draw a circle with radius . Construct tangents to the circle from a point at a distance from the centre.
Answer :
Steps of construction :
Step 1: Draw a circle of radius with centre .
Step 2 : Take a point in the exterior of the circle such that .
Step 3: Draw segment OP. Draw perpendicular bisector of segment OP to get its midpoint .
Step 4: Draw a circle with radius and centre .

Step 5: Name the point of intersection of the two circles as A and B.
Step 6: Join PA and PB.
Thus and are required tangents.
(iv) A metal cuboid of measures was melted to make coins. How many coins were made, if the thickness and diameter of each coin was and respectively?
Answer : Answer is not given due to the change in reduced syllabus.
4. Solve the following sub-questions (Any two) :
(i) In is a line segment intersecting at and at such that seg seg . If divides into two equal parts having equal areas, find .
Answer : In above figure
and
and
In and
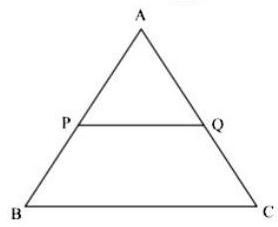
Now,
From (i) and (ii)
Let
and
Now,
From (iii) and (iv)
(ii) Draw a circle of radius and draw a chord of length . Draw tangents at points and without using centre.
Answer :
Steps of construction :
Step 1: Draw a circle of with centre and radius .
Step 2: Draw a chord PQ of length
Step 3: Taking a point on the major arc , join and .
Step 4: Make and .
Step 5 : Produce TP to and to .
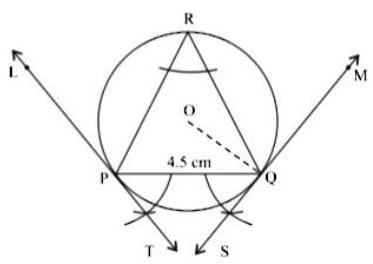
Hence, TPL and SQM are the required tangents.
(iii) In the figure given is a square of side . Points are midpoints of side , side , side , side respectively. Find area of shaded region. *

Answer : Answer is not given due to the change in reduced syllabus.
5. Solve the following sub-questions (Any one) :
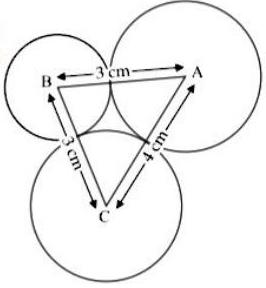
(i) Circles with centres and touch each other externally. If , , then find the radii of each circle.
Answer : Suppose radius of circle with centre A is

(ii) If
show that :