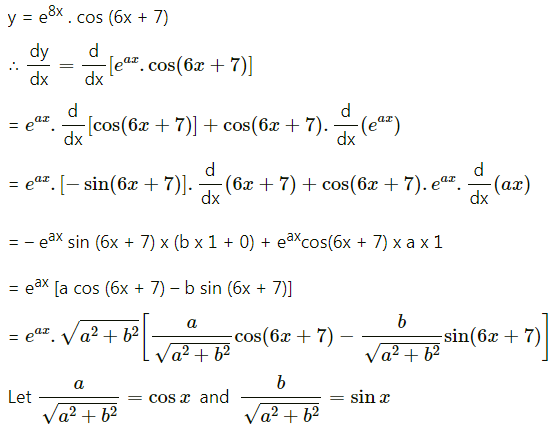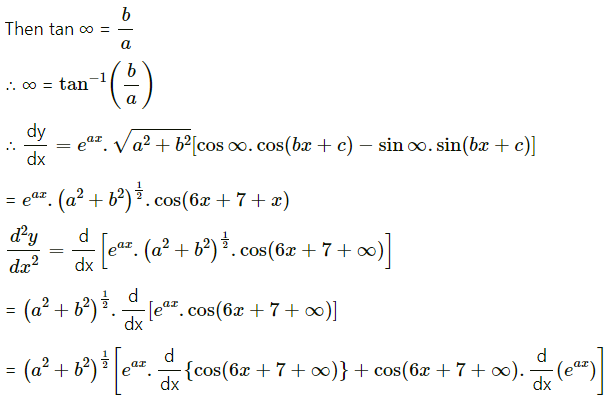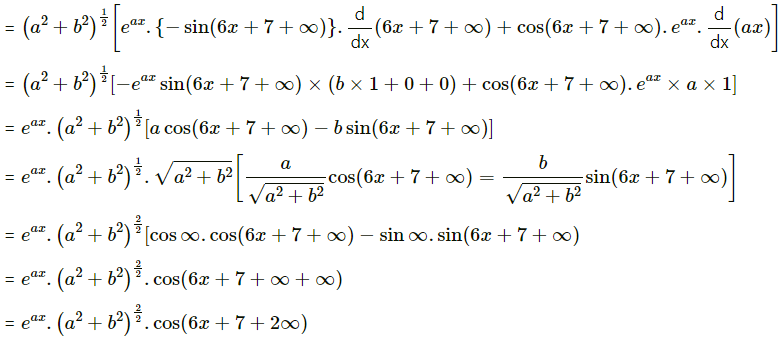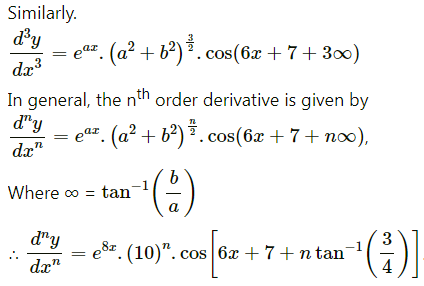Chapter 1 Differentiation Ex 1.5
Chapter 1 Differentiation Ex 1.5
Question 1.
Find the second order derivatives of the following: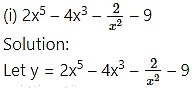
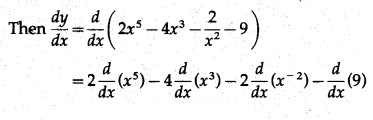
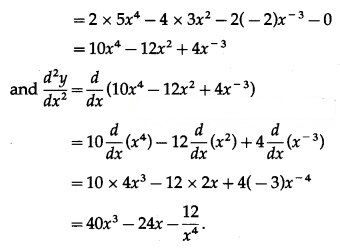
(ii) . tan x
Solution:
Let y = . tan x
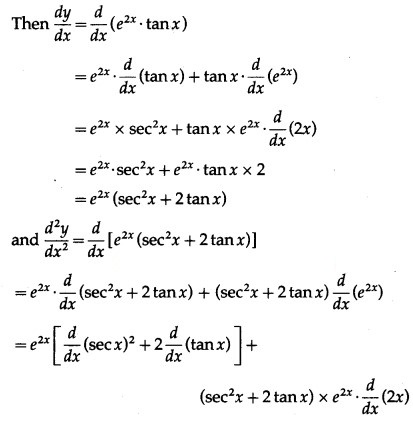
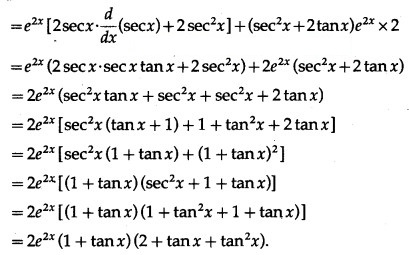
(iii) . cos 5x
Solution:
Let y = . cos 5x
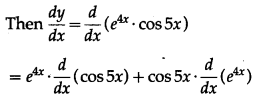
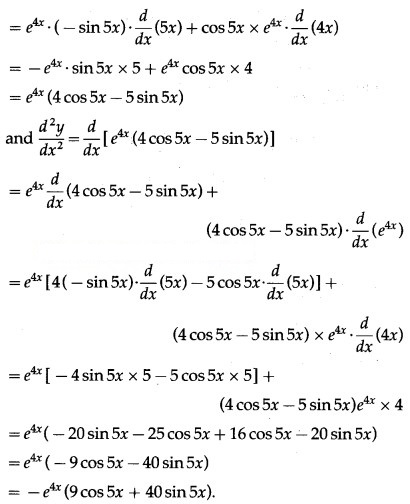
(iv) . log x
Solution:
Let y = . log x
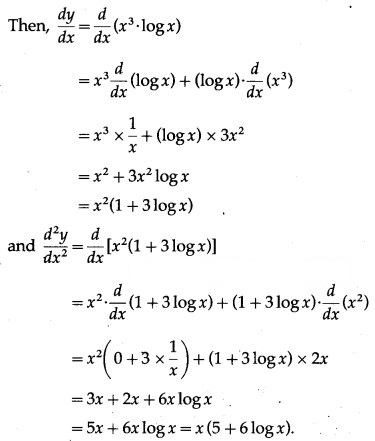
(v) log(log x)
Solution:
Let y = log(log x)
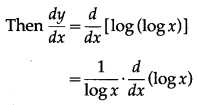
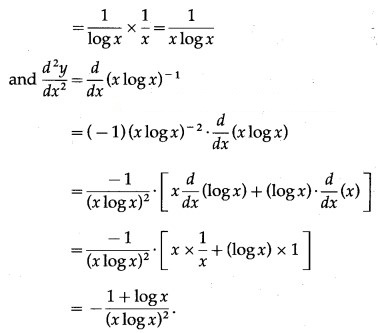
(vi)
Solution:
y =
log y = log = x log x
Differentiating both sides w.r.t. x, we get
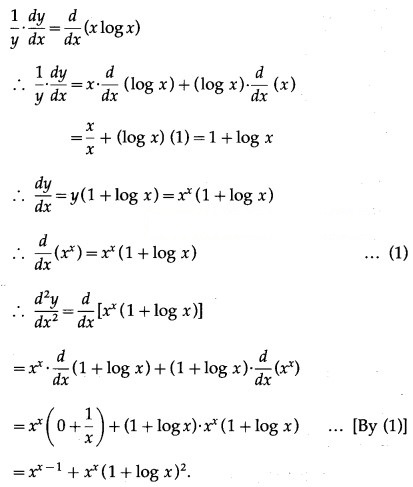
Question 2.
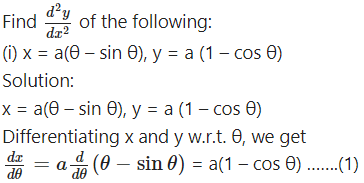
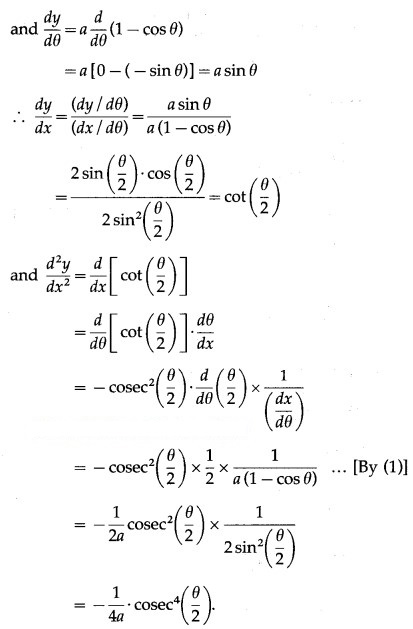
(ii) x = 2a, y = 4at
Solution:
x = 2a, y = 4at
Differentiating x and y w.r.t. t, we get
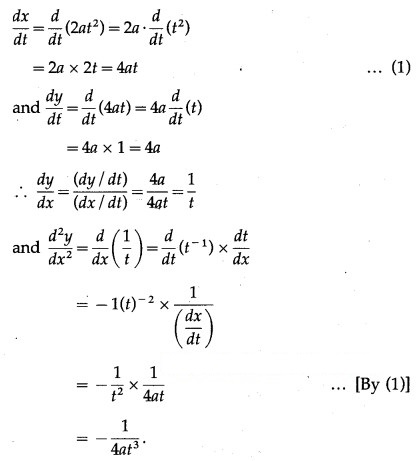
![]()
Solution:
x = sin θ, y = θ
Differentiating x and y w.r.t. θ, we get,
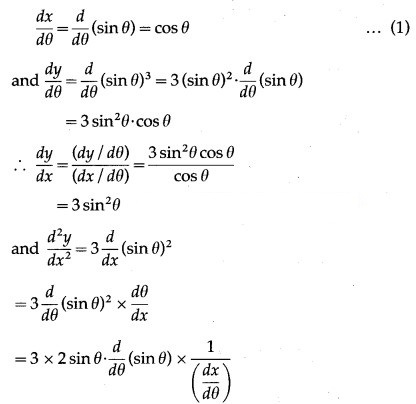
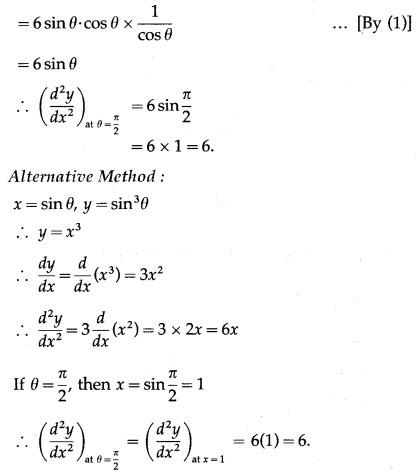
![]()
Solution:
x = a cos θ, y = b sin θ
Differentiating x and y w.r.t. θ, we get
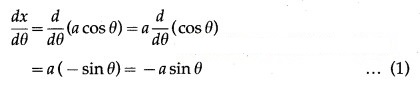
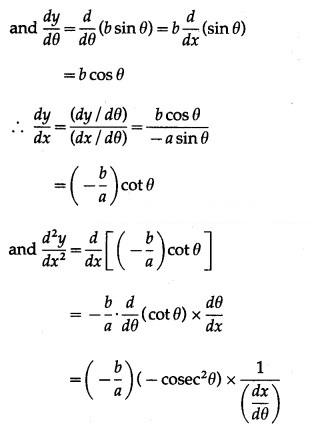
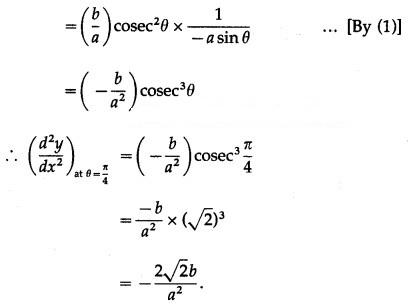
Question 3.

Differentiating x and y w.r.t. t, we get
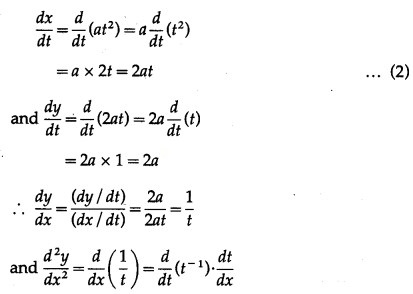
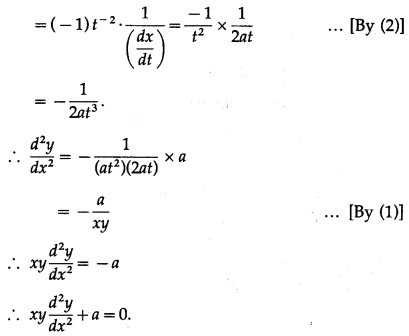
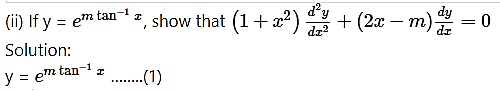

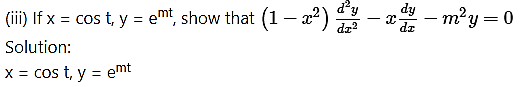
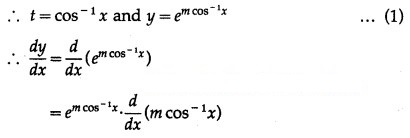

![]()
Solution:
y = x + tan x
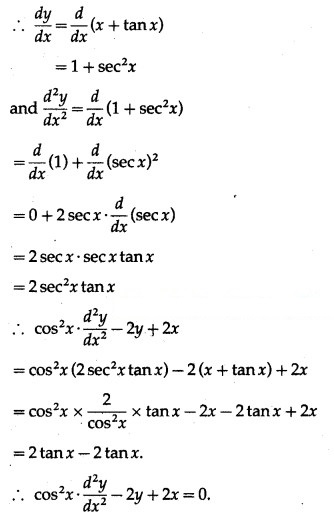

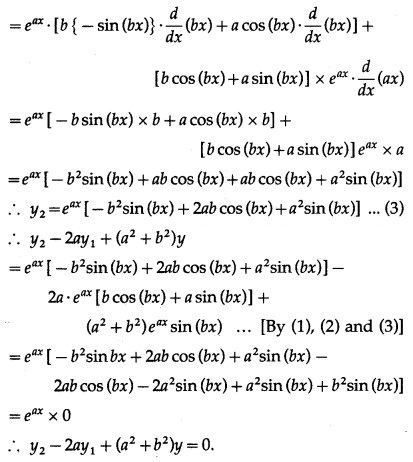
![]()
Solution:
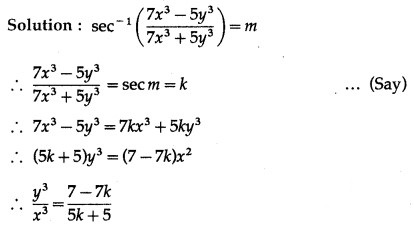
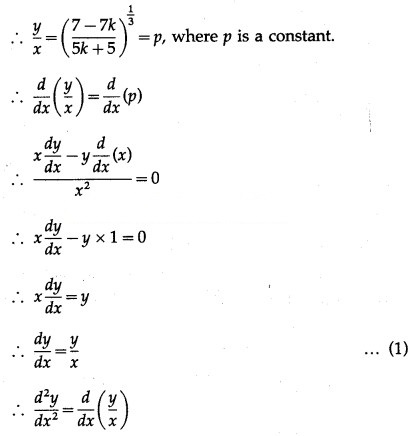

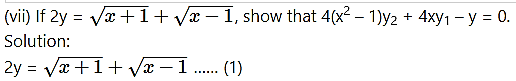
Differentiating both sides w.r.t. x, we get
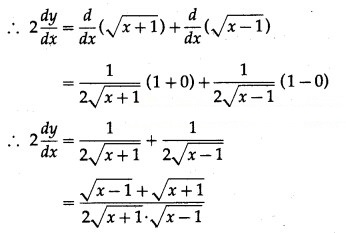

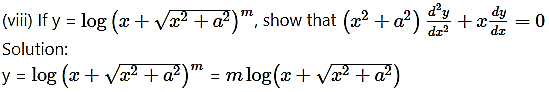

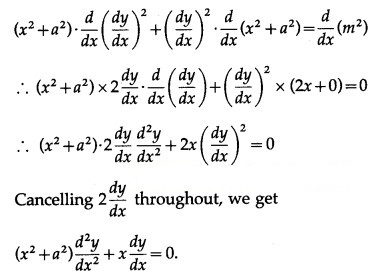
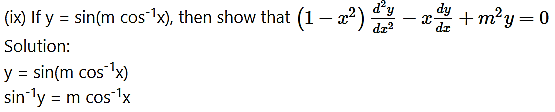
Differentiating both sides w.r.t. x, we get

(x) If y = log(log 2x), show that x + (1 + x) = 0.
Solution:
y = log(log 2x)
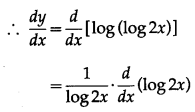
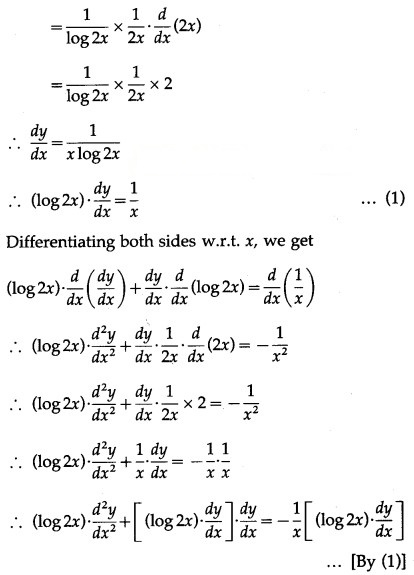
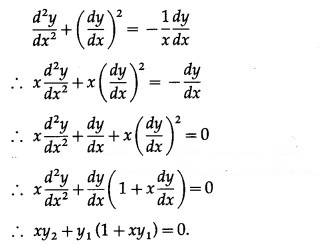
Differentiating both sides w.r.t. x, we get


![]()
Solution:
x = a sin t – b cos t, y = a cos t + b sin t
Differentiating x and y w.r.t. t, we get
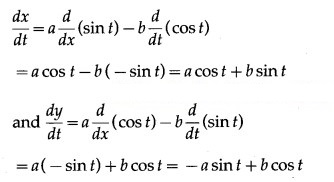

Question 4.
Find the nth derivative of the following:
(i) (ax +
Solution:
Let y = (ax +
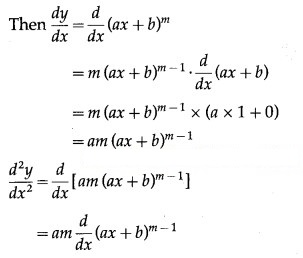
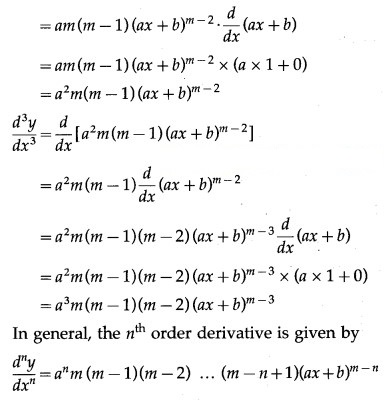

(ii) 1/x
Solution:
Let y = 1/x

(iii)
Solution:
Let y =
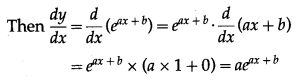

(iv)
Solution:
Let y =
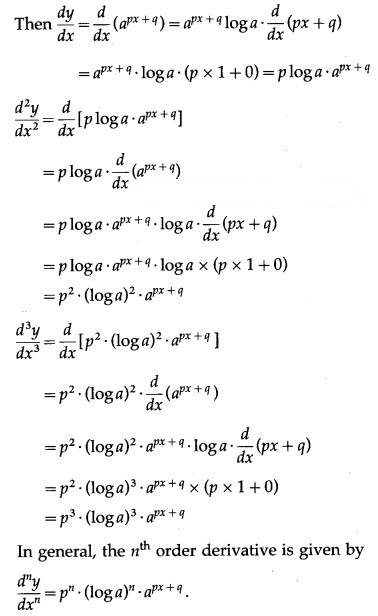
(v) log(ax + b)
Solution:
Let y = log(ax + b)
![]()
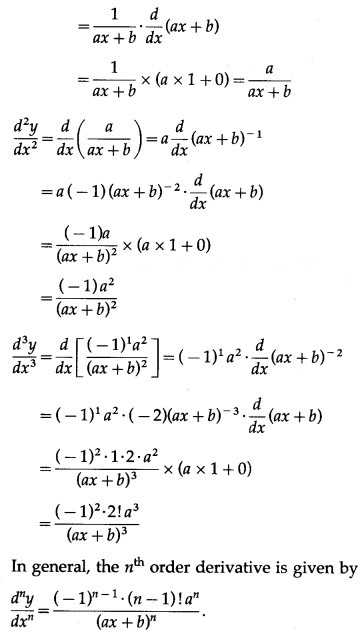
(vi) cos x
Solution:
Let y = cos x

(vii) sin(ax + b)
Solution:
Let y = sin(ax + b)
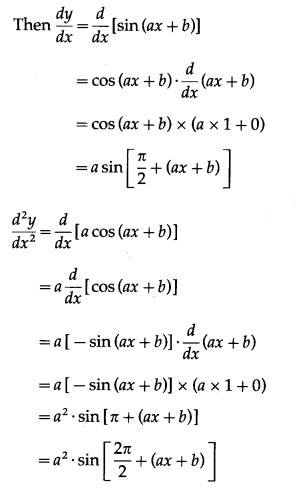
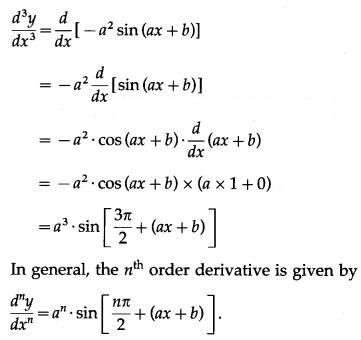
(viii) cos(3 – 2x)
Solution:
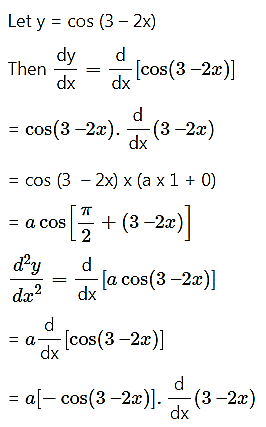
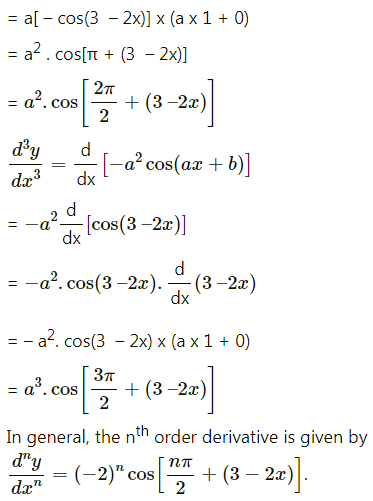
(ix) log(2x + 3)
Solution:
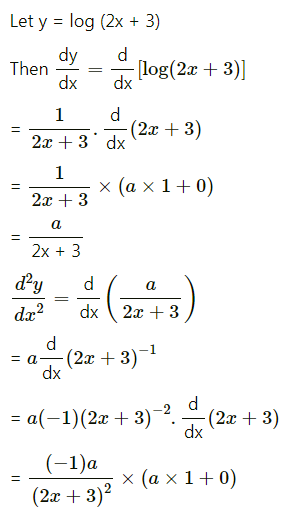

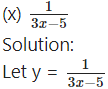
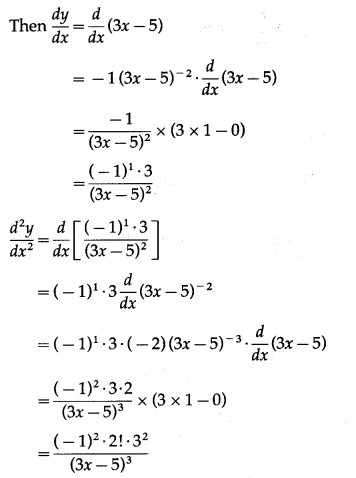
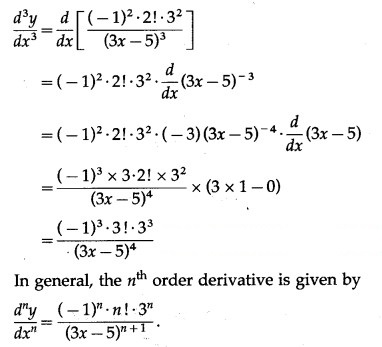
(xi) y = . cos (bx + c)
Solution:
y = . cos (bx + c)
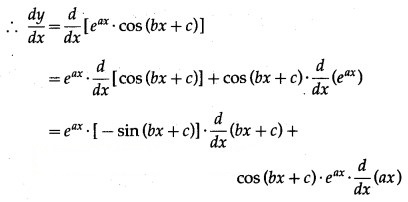

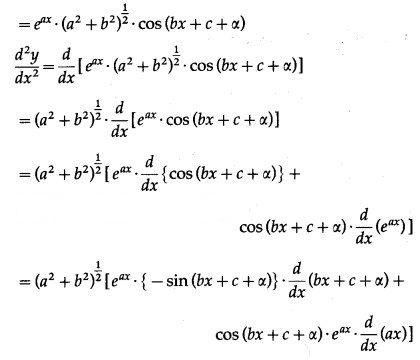

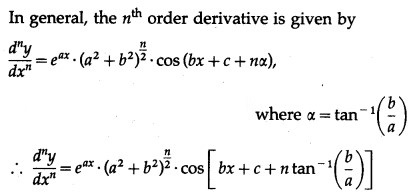
(xii) y = . cos (6x + 7)
Solution: