Blog

Chapter 1 Angle and its Measurement Ex 1.2

Chapter 1 Angle and its Measurement Ex 1.2

Question 1.
Find the length of an arc of a circle which subtends an angle of 108° at the centre, if the radius of the circle is 15 cm.
Solution:
Here, r = 15cm and

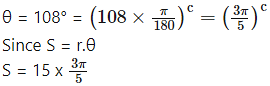
= 9π cm.

Question 2.
The radius of a circle is 9 cm. Find the length of an arc of this circle which cuts off a chord of length equal to length of radius.
Solution:
Here, r = 9cm
Let the arc AB cut off a chord equal to the radius of the circle.
Since OA = OB = AB,
ΔOAB is an equilateral triangle.
m∠AOB = 60°
θ = 60°

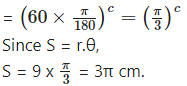
Question 3.
Find the angle in degree subtended at the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm.
Solution:
Here, r = 25 cm and S = 15 cm
Since S = r.θ,
15 = 25 x θ

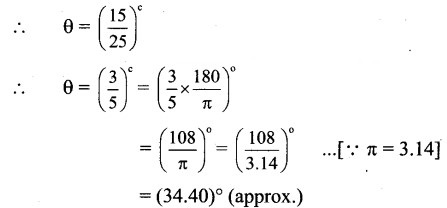
Question 4.
A pendulum of length 14 cm oscillates through an angle of 18°. Find the length of its path.
Solution:

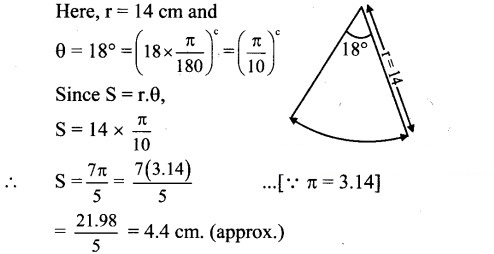
Question 5.
Two arcs of the same length subtend angles of 60° and 75° at the centres of the two circles. What is the ratio of radii of two circles?
Solution:
Let , and  be the radii of the two circles and let their arcs of same length S subtend angles of 60° and 75° at their centres.
Angle subtended at the centre of the first circle,

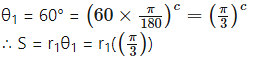
Angle subtended at the centre of the second circle,

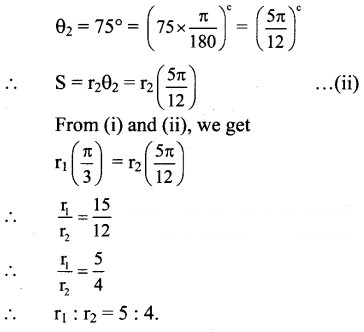
Question 6.
The area of the circle is 2571 sq.cm. Find the length of its arc subtending an angle of 144° at the centre. Also find the area of the corresponding sector.
Solution:
Area of circle = πr²
But area is given to be 25 π sq.cm
∴ 25π = πr²
∴ r² = 25
∴ r = 5 cm

Question 7.
OAB is a sector of the circle having centre at O and radius 12 cm. If m∠AOB = 45°, find the difference between the area of sector OAB and ΔAOB.
Solution:
Here, r = 12 cm


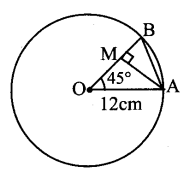
Draw AM ⊥ OB
In ΔOAM,

[Note: The question has been modified.]

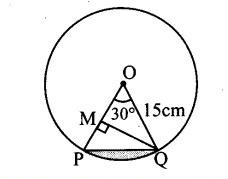
Question 8.
OPQ is the sector of a circle having centre at O and radius 15 cm. If m∠POQ = 30°, find the area enclosed by arc PQ and chord PQ.
Solution:
Here, r = 15 cm
m∠POQ = 30°
\(\left(30 \times \frac{\pi}{180}\right)^{c}[/larex]

∴ θ = [latex]\left(\frac{\pi}{6}\right)^{c}\)
Draw QM ⊥ OP
In ΔOQM,

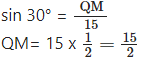
Shaded portion indicates the area enclosed by arc PQ and chord PQ.
∴ A(shaded portion)
= A(sector OPQ) – A(ΔOPQ)

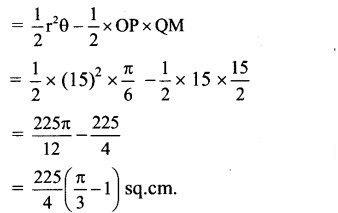
Question 9.
The perimeter of a sector of the circle of area 25π sq.cm is 20 cm. Find the area of sector.
Solution:
Area of circle = π
But area is given to be 25π sq.cm.
∴ 25π = π
∴  = 25
∴ r = 5 cm
Perimeter of sector = 2r + S
But perimeter is given to be 20 cm.
∴ 20 = 2(5) + S
∴ 20 = 10 + S
∴ S = 10 cm
Area of sector =1/2  x r x S
=1/2  x 5 x 10
= 25sq.cm.

Question 10.
The perimeter of a sector of the circle of area 64 7i sq.cm is 56 cm. Find the area of the sector.
Solution:
Area of circle = π 
But area is given to be 25π sq.cm.
∴ 64π = π 
∴   = 64
∴ r = 8 cm
Perimeter of sector = 2r + S
But perimeter is given to be 20 cm.
∴ 56 = 2(5) + S
∴ 56 = 16 + S
∴ S = 40 cm
Area of sector =1/2  x r x S
=1/2 x 8 x 40
= 160sq.cm.