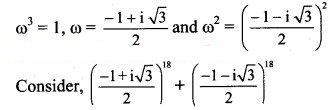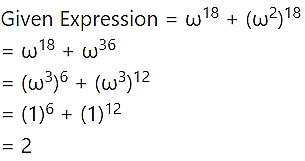Chapter 1 Complex Numbers Miscellaneous Exercise 1
Chapter 1 Complex Numbers Miscellaneous Exercise 1
(I) Select the correct answer from the given alternatives.
Question 1.
If n is an odd positive integer, then the value of 1 + is:
(A) -4i
(B) 0
(C) 4i
(D) 4
Answer:
(B) 0
Hint:
= 1 – 1 + 1 – 1 …..(n odd positive integer)
= 0
Question 2.
(A) -2
(B) 1
(C) 0
(D) -1
Answer:
(D) -1
Hint:
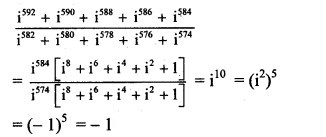
Question 3.
√-3 √-6 is equal to
(A) -3√2
(B) 3√2
(C) 3√2 i
(D) -3√2 i
Answer:
(A) -3√2
Hint:
√-3 √-6
= (√3 i) (√6 i)
= 3√2 (-1)
= -3√2
Question 4.
If ω is a complex cube root of unity, then the value of is:
(A) -1
(B) 1
(C) 0
(D) 3
Answer:
(C) 0
Hint:
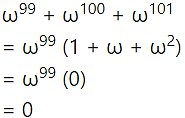
Question 5.
(A) cos 2θ
(B) 2cos 2θ
(C) 2cos θ
(D) 2sin θ
Answer:
(B) 2cos 2θ
Hint:
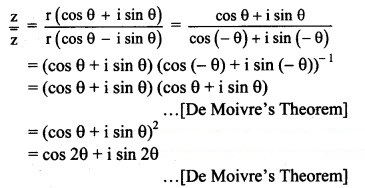
Question 6.
If ω(≠1) is a cube root of unity and (1 + ω = A + Bω, then A and B are respectively the numbers
(A) 0, 1
(B) 1, 1
(C) 1, 0
(D) -1, 1
Answer:
(B) 1, 1
Hint:
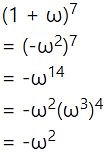
= 1 + ω
A = 1, B = 1
Question 7.
Hint:
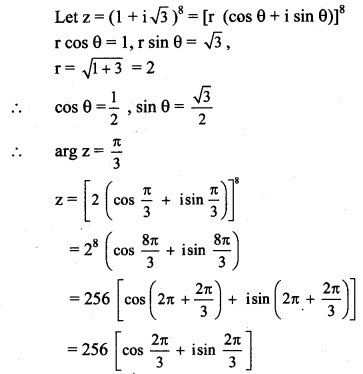
Question 8.
(A) -θ
(B) θ
(C) π – θ
(D) π + θ
Answer:
(A) -θ
Hint:
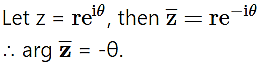
Question 9.
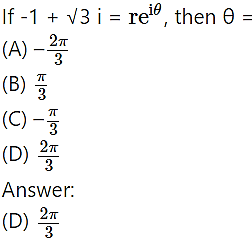
Hint:
Question 10.
If z = x + iy and |z – zi| = 1, then
(A) z lies on X-axis
(B) z lies on Y-axis
(C) z lies on a rectangle
(D) z lies on a circle
Answer:
(D) z lies on a circle
Hint:
|z – zi | = |z| |1 – i| = 1
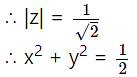
(II) Answer the following:
Question 1.
Simplify the following and express in the form a + ib.
(i) 3 + √-64
Solution:
3 + √-64
= 3 + √64 √-1
= 3 + 8i
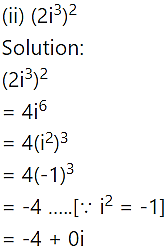
(iii) (2 + 3i) (1 – 4i)
Solution:
(2 + 3i)(1 – 4i)
= 2 – 8i + 3i – 12
= 2 – 5i – 12(-1) …..[∵ = -1]
= 14 – 5i
Solution:
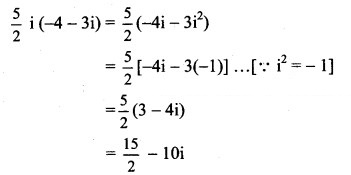
= (-8 + 6i)(3 + i)
= -24 – 8i + 18i + 6i2
= -24 + 10i + 6(-1)
= -24 + 10i – 6
= -30 + 10i
Solution:
Solution:
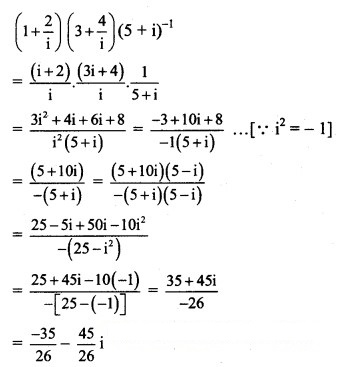
Solution:
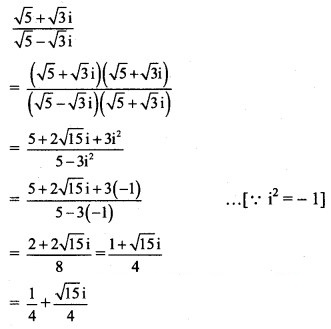
Solution:
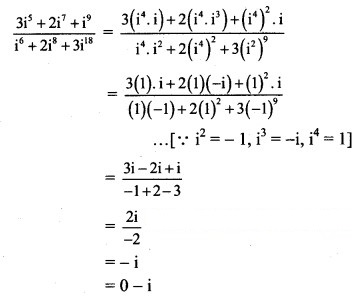
Solution: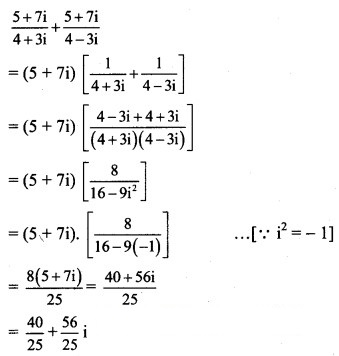
Question 2.
Solve the following equations for x, y ∈ R
(i) (4 – 5i)x + (2 + 3i)y = 10 – 7i
Solution:
(4 – 5i)x + (2 + 3i)y = 10 – 7i
(4x + 2y) + (3y – 5x) i = 10 – 7i
Equating real and imaginary parts, we get
4x + 2y= 10 i.e., 2x + y = 5 ……(i)
and 3y – 5x = -7 ……(ii)
Equation (i) × 3 – equation (ii) gives
11x = 22
∴ x = 2
Putting x = 2 in (i), we get
2(2) + y = 5
∴ y = 1
∴ x = 2 and y = 1
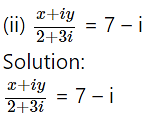
x + iy = (7 – i)(2 + 3i)
x + iy = 14 + 21i – 2i – 3
x + iy = 14 + 19i – 3(-1)
x + iy = 17 + 19i
Equating real and imaginary parts, we get
∴ x = 17 and y = 19
(iii) (x + iy) (5 + 6i) = 2 + 3i
Solution:
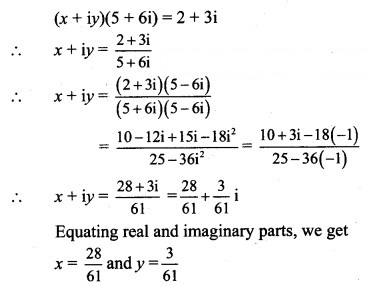
2x + 2yi – y + xi = 10
(2x – y) + (x + 2y)i = 10 + 0 . i
Equating real and imaginary parts, we get
2x – y = 10 ……(i)
and x + 2y = 0 ……..(ii)
Equation (i) × 2 + equation (ii) gives, we get
5x = 20
∴ x = 4
Putting x = 4 in (i), we get
2(4) – y = 10
y = 8 – 10
∴ y = -2
∴ x = 4 and y = -2
Question 3.
Evaluate
(i) (1 – i +
Solution:
Question 4.
Find the value of
(i) + 2 – 3x + 21, if x = 1 + 2i
Solution:
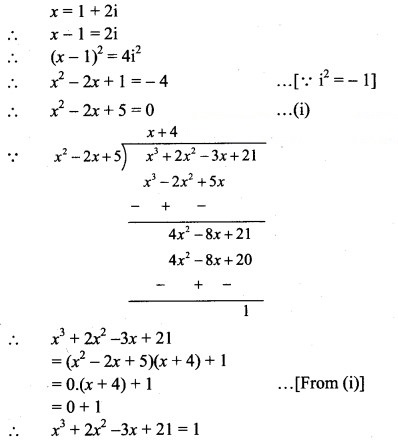
(ii) + 9 + 35 – x + 164, if x = -5 + 4i
Solution:
Question 5.
Find the square roots of
(i) -16 + 30i
Solution:
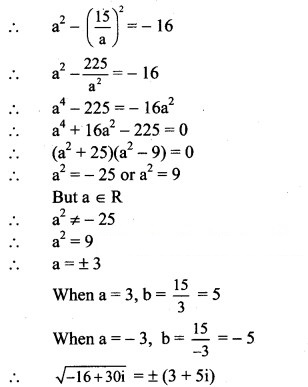
(ii) 15 – 8i
Solution:
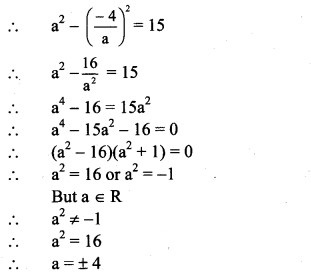
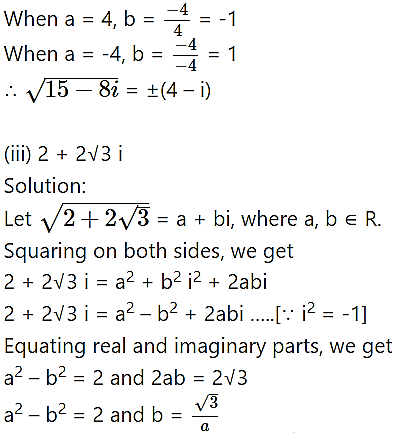
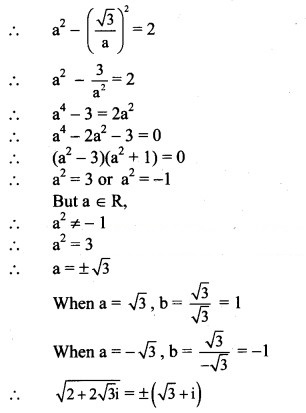
(iv) 18i
Solution:
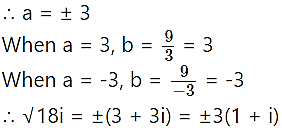
(v) 3 – 4i
Solution:
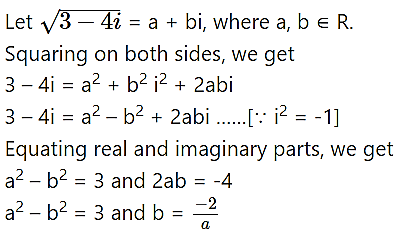
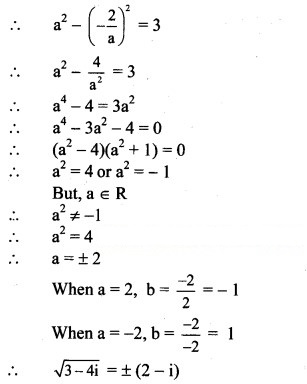
(vi) 6 + 8i
Solution:
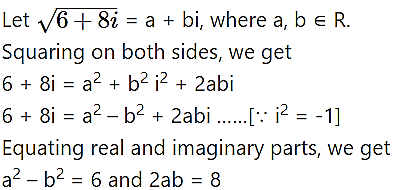
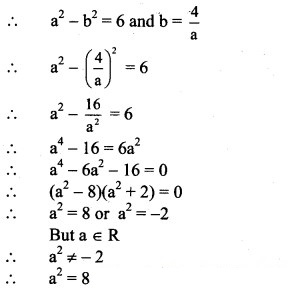
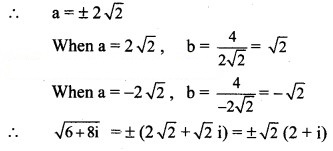
Question 6.
Find the modulus and argument of each complex number and express it in the polar form.
(i) 8 + 15i
Solution:
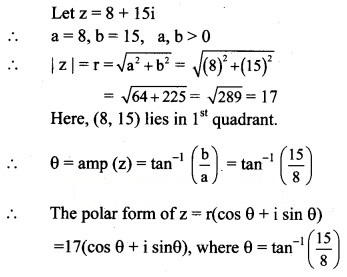
(ii) 6 – i
Solution: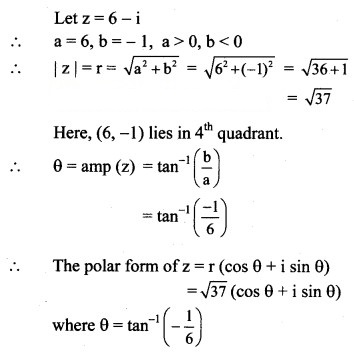
Solution:
Solution:
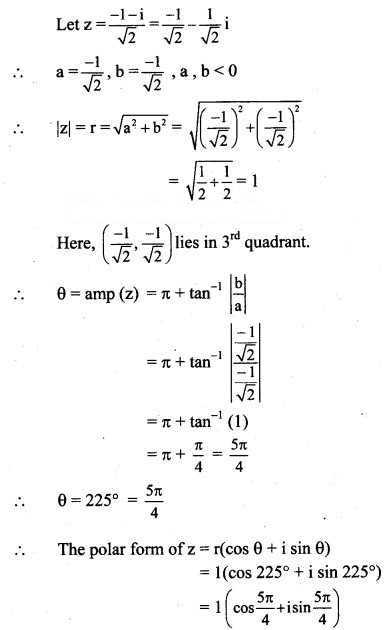
(v) 2i
Solution:
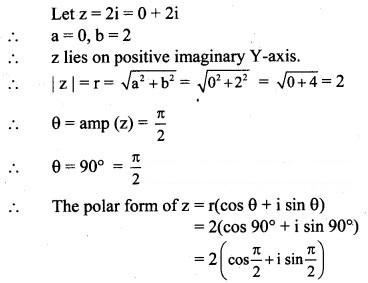
(vi) -3i
Solution: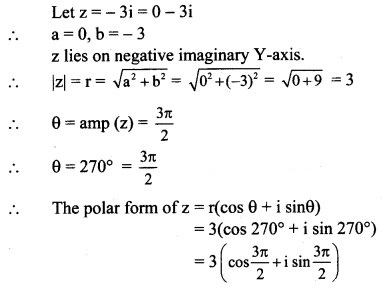
Solution:
Question 7.
Represent 1 + 21, 2 – i, -3 – 2i, -2 + 3i by points in Argand’s diagram.
Solution:
The complex numbers 1 + 2i, 2 – i, -3 – 2i, -2 + 3i will be represented by the points A(1, 2), B(2, -1), C(-3, -2), D(-2, 3) respectively as shown below:
Question 8.
Solution:
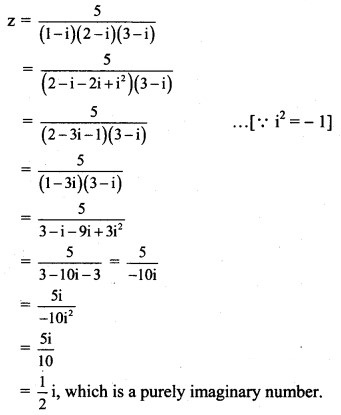
Question 9.
Find the real numbers x and y such that
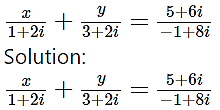
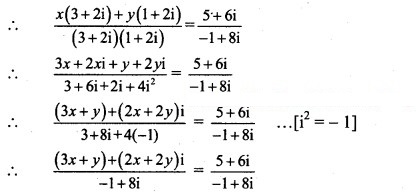
(3x + y) + 2(x + y)i = 5 + 6i
Equating real and imaginary parts, we get
3x + y = 5 ……(i)
and 2(x + y) = 6
i.e., x + y = 3 …….(ii)
Subtracting (ii) from (i), we get
2x = 2
∴ x = 1
Putting x = 1 in (ii), we get
1 + y = 3
∴ y = 2
∴ x = 1, y = 2
Question 10.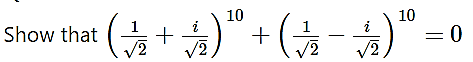
Solution:
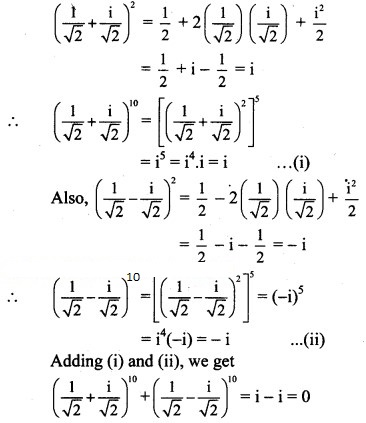
Question 11.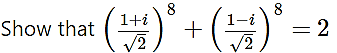
Solution:
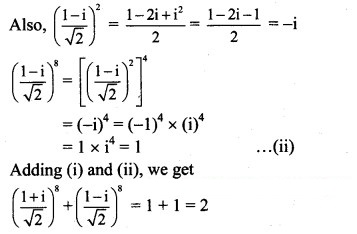
Question 12.
Convert the complex numbers in polar form and also in exponential form.
Solution:
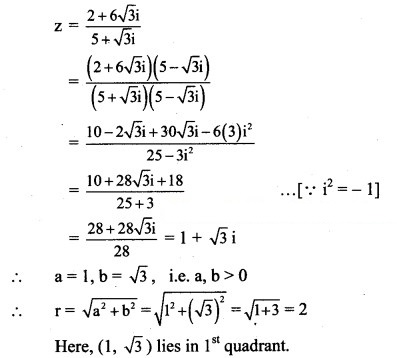
(ii) z = -6 + √2 i
Solution:
z = -6 + √2 i
∴ a = -6, b = √2
i.e. a < 0, b > 0
Solution:
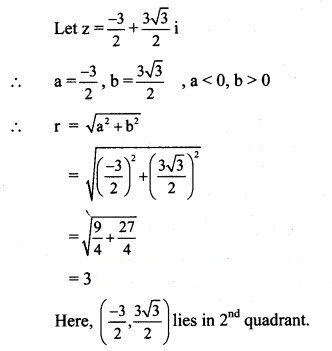
Question 13.
Solution:
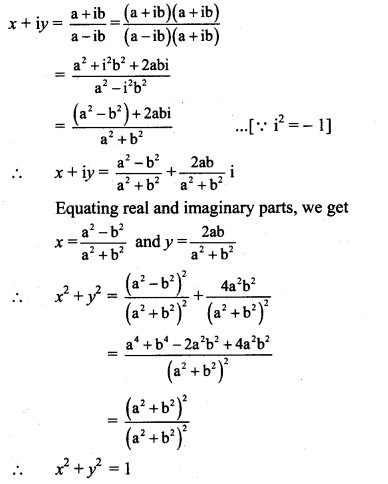
Question 14.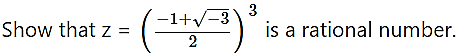
Solution:
Question 15.
Solution:
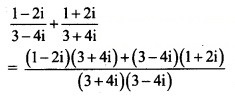
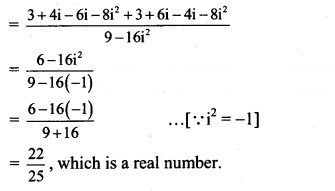
Question 16.
Simplify
Solution:
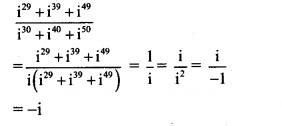
Solution: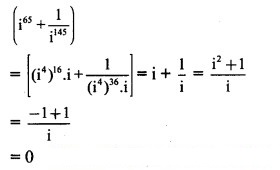
Solution: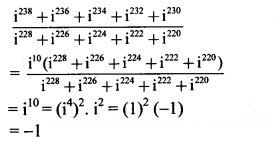
Question 17.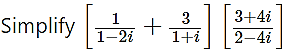
Solution:
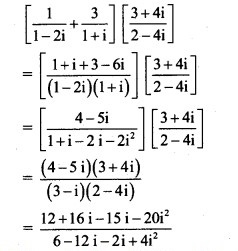
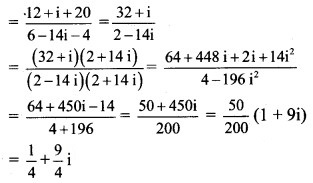
Question 18.
If α and β are complex cube roots of unity, prove that (1 – α) (1 – β) (1 – ) (1 –) = 9.
Solution:
α and β are the complex cube roots of unity.
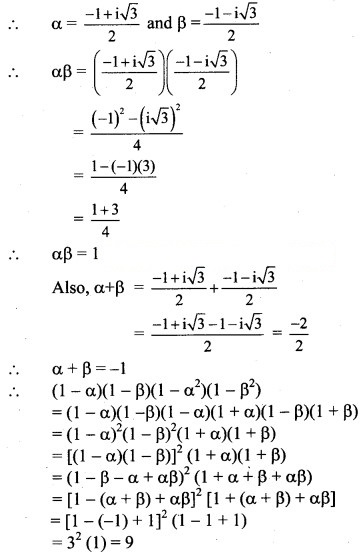
Question 19.
Question 20.
If ω is the cube root of unity, then find the value of
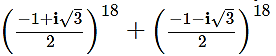
Solution:
If ω is the complex cube root of unity, then
