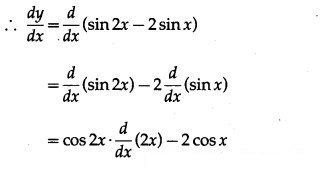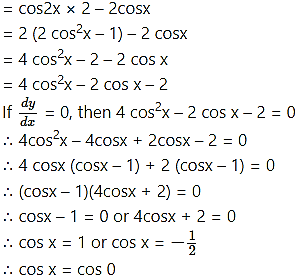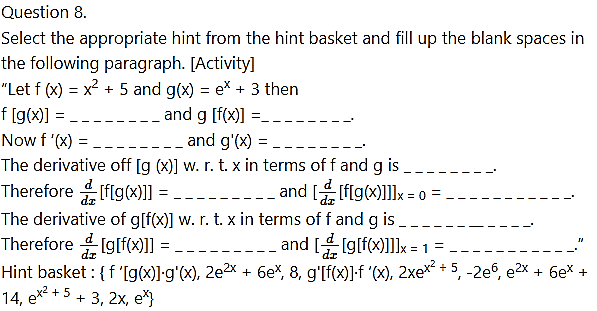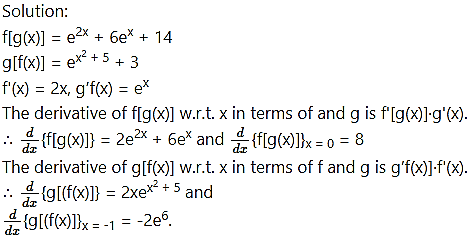Blog

Chapter 1 Differentiation Ex 1.1

Chapter 1 Differentiation Ex 1.1

Question 1.
Differentiate the following w.r.t. x :
(i)
Solution:
Method 1:
Let y =
Put u =  – 2x – 1. Then y =

Method 2:
Let y =

Differentiating w.r.t. x, we get

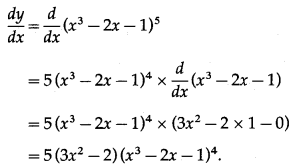
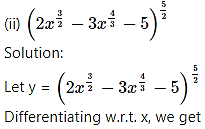
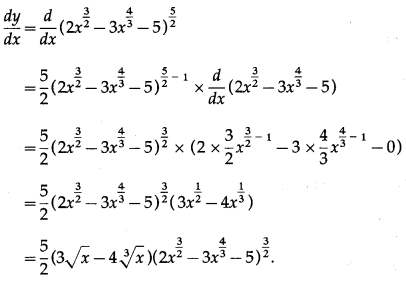
Solution:

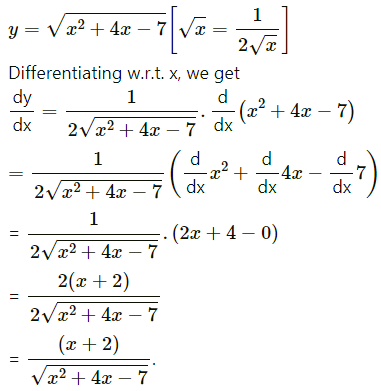
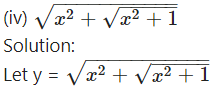
Differentiating w.r.t. x, we get

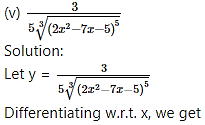
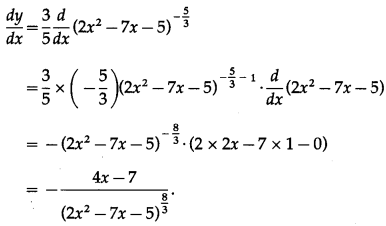
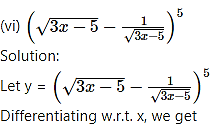
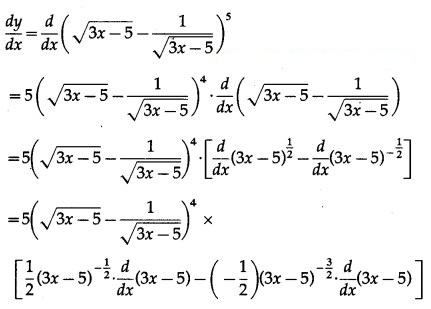
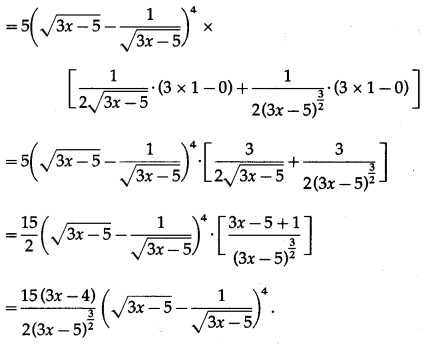
Question 2.

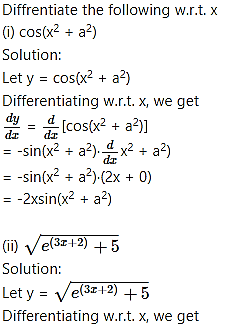
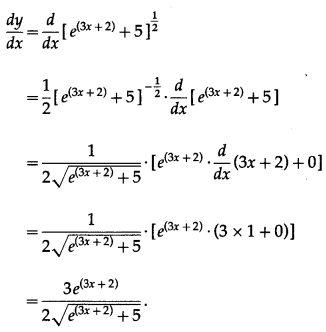
Differentiating w.r.t. x, we get

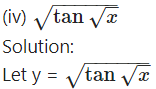
Differentiating w.r.t. x, we get

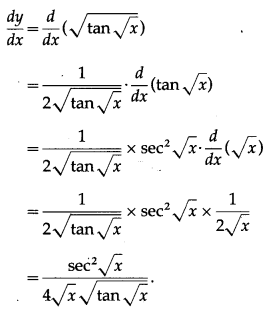
(v)

Solution:
Let y =
Differentiating w.r.t. x, we get

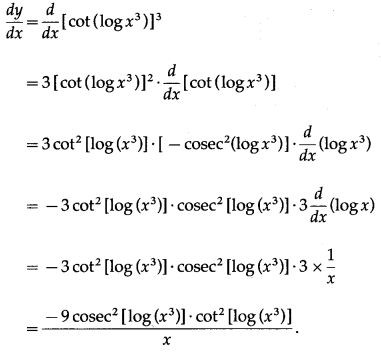
(vi)
Solution:
Let y =
Differentiating w.r.t. x, we get

Differentiating w.r.t. x, we get

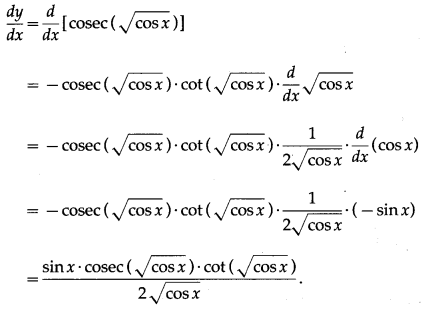
(viii) log[cos ( – 5)]
Solution:
Let y = log[cos ( – 5)]
Differentiating w.r.t. x, we get

(ix)
Solution:
Let y =

Differentiating w.r.t. x, we get

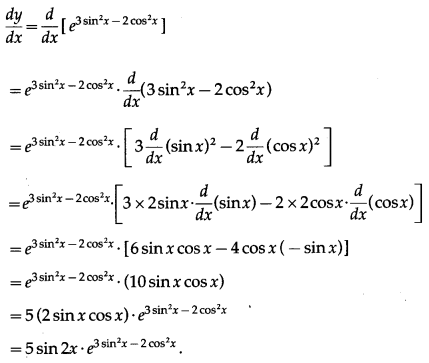
(x) [log (+ 7)]
Solution:
Let y = [log (+ 7)]
Differentiating w.r.t. x, we get

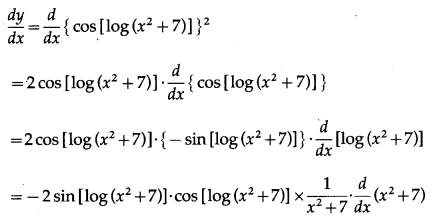
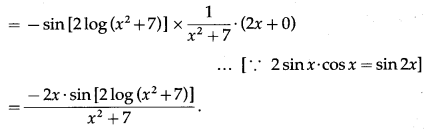
(xi) tan[cos (sinx)]
Solution:
Let y = tan[cos (sinx)]
Differentiating w.r.t. x, we get

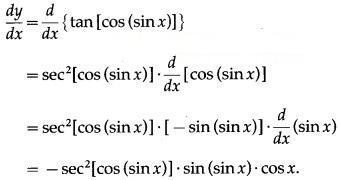
(xii) sec[tan ( + 4)]
Solution:
Let y = sec[tan ( + 4)]
Differentiating w.r.t. x, we get

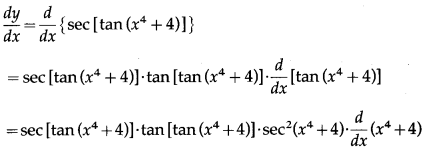
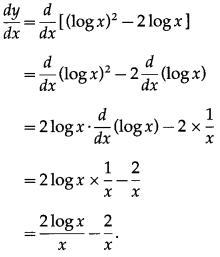
Differentiating w.r.t. x, we get

(xv) log[sec()]
Solution:
Let y = log[sec()]
Differentiating w.r.t. x, we get

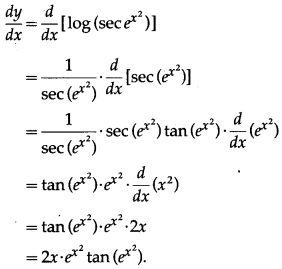
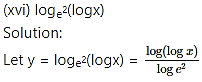
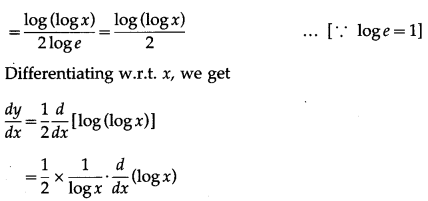
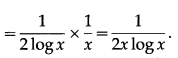
(xvii) [log{log(logx)}
Solution:
let y = [log{log(logx)}
Differentiating w.r.t. x, we get

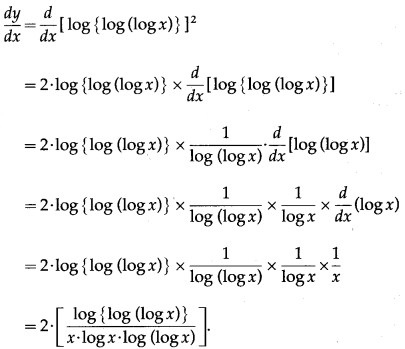
(xviii)
Solution:
Let y =
Differentiating w.r.t. x, we get

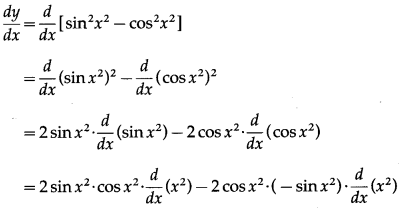
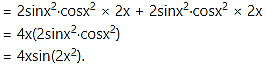
Question 3.
Diffrentiate the following w.r.t. x
(i) (x² + 4x + 1 
Solution:
Let y = (x² + 4x + 1 

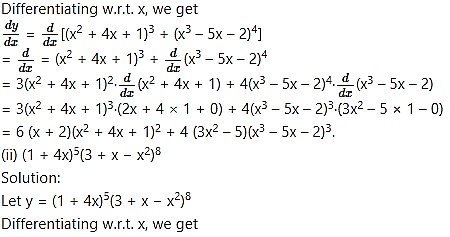
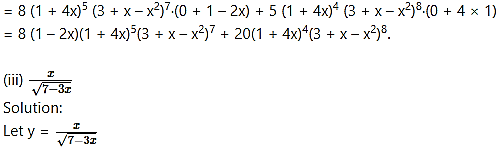
Differentiating w.r.t. x, we get

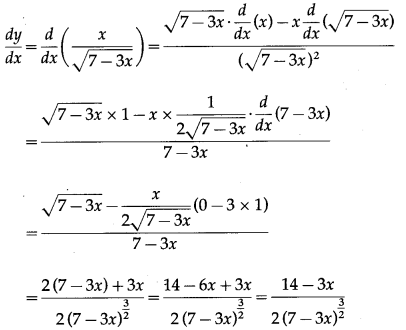
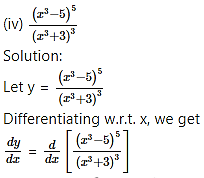
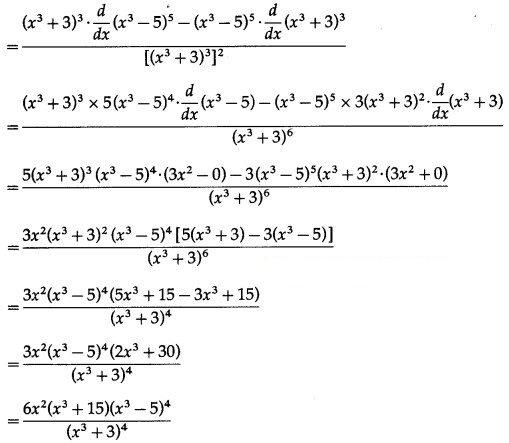
(v) (1 +

Solution:
Let y = (1 +
Differentiating w.r.t. x, we get

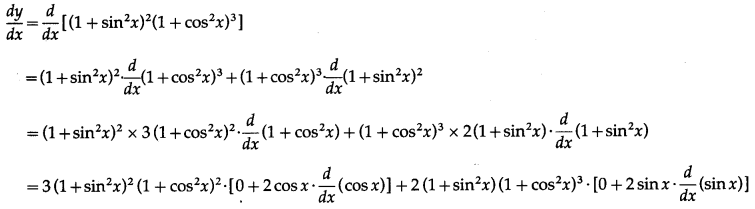
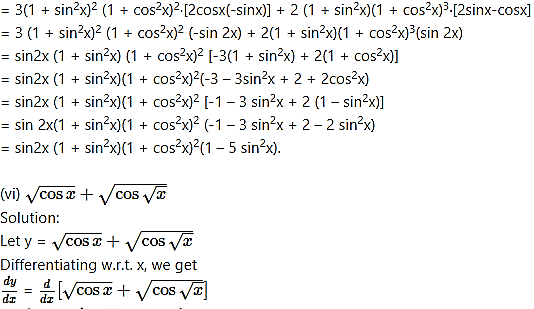
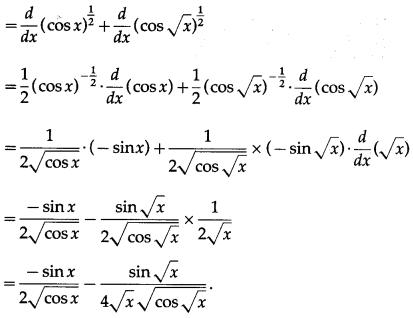
(vii) log(sec 3x+ tan 3x)
Solution:
Let y = log(sec 3x+ tan 3x)
Differentiating w.r.t. x, we get

Solution:

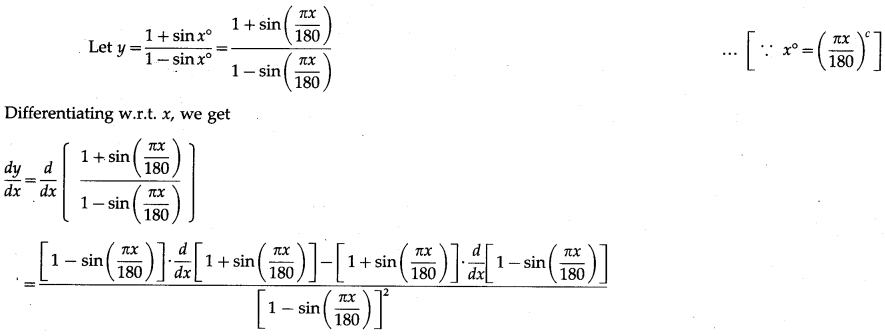
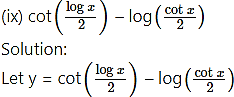
Differentiating w.r.t. x, we get

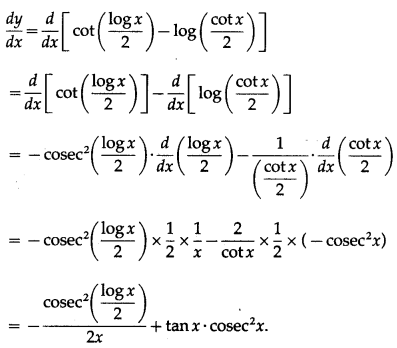
Solution:

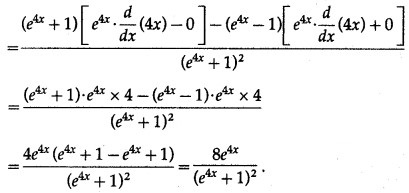
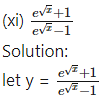
Differentiating w.r.t. x, we get

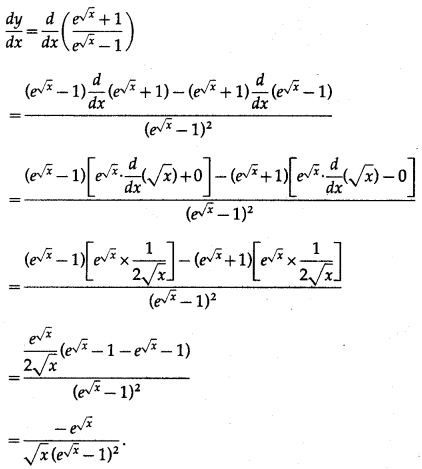
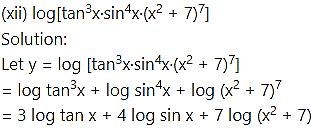
Differentiating w.r.t. x, we get

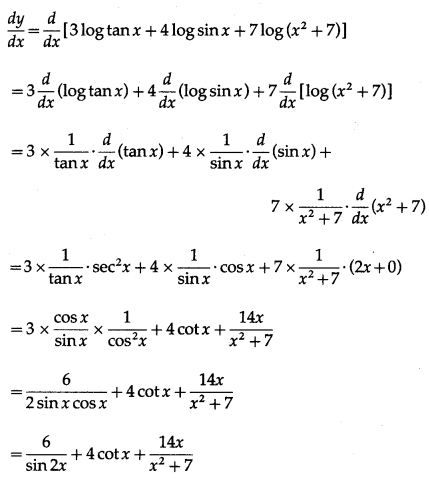
= 6cosec2x + 4 cotx + 

Solution:

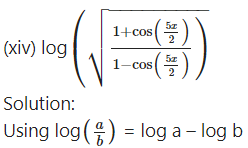
log  = b log a

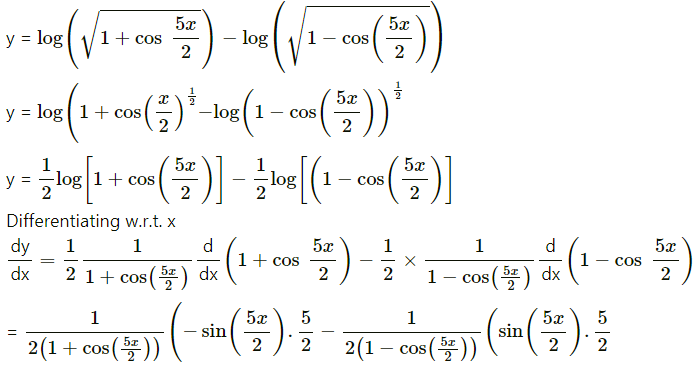
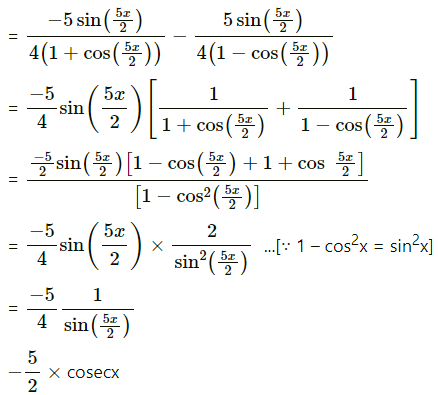
Solution:

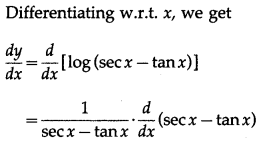
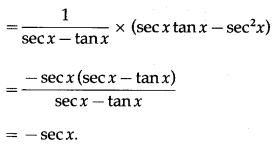
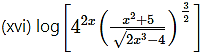
Solution:

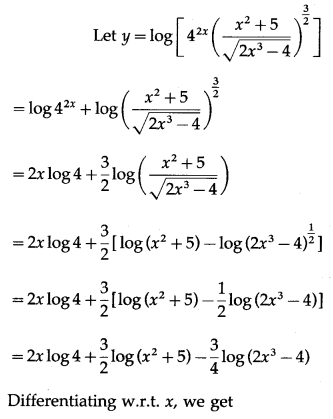
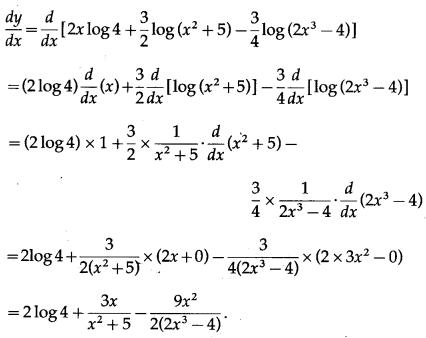
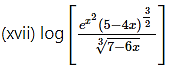
Solution:

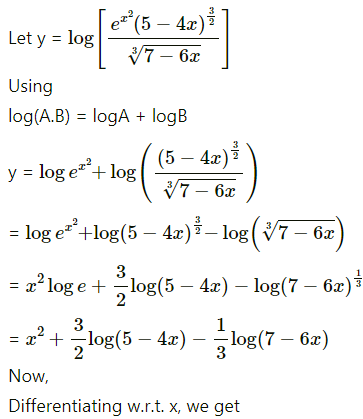
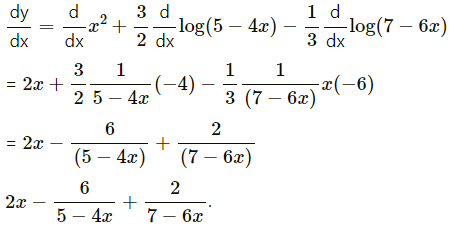
Solution:

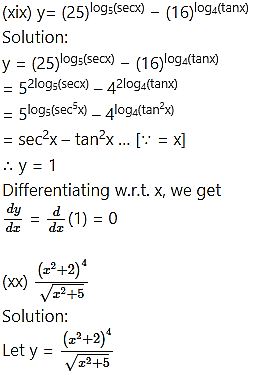
Differentiating w.r.t. x, we get

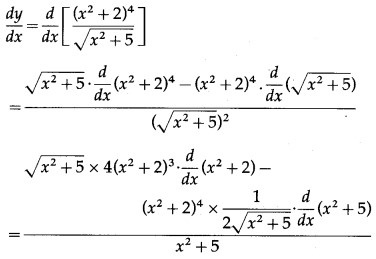
Question 4.
A table of values of f, g, f ‘ and g’ is given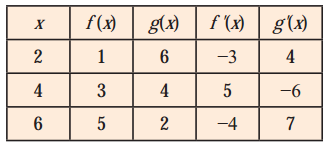

(i) If r(x) = f [g(x)] find r’ (2).
Solution:
r(x) = f[g(x)]

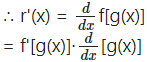
= f'[g(x)∙[g'(x)]
∴ r'(2) = f'[g(2)]∙g'(2)
= f'(6)∙g'(2) … [∵ g(x) = 6, when x = 2]
= -4 × 4 … [From the table]
= -16.

(ii) If R(x) = g[3 + f(x)] find R’ (4).
Solution:
R(x) = g[3 + f(x)]

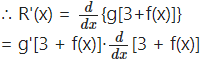
= g'[3 +f(x)]∙[0 + f'(x)]
= g'[3 + f(x)]∙f'(x)
∴ R'(4) = g'[3 + f(4)]∙f'(4)
= g'[3 + 3]∙f'(4) … [∵ f(x) = 3, when x = 4]
= g'(6)∙f'(4)
= 7 × 5 … [From the table]
= 35.

(iii) If s(x) = f[9− f(x)] find s’ (4).
Solution:
s(x) = f[9− f(x)]

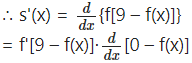
= f'[9 – f(x)]∙[0 – f'(x)]
= -f'[9 – f(x)] – f'(x)
∴ s'(4) = -f'[9 – f(4)] – f'(4)
= -f'[9 – 3] – f'(4) … [∵ f(x) = 3, when x = 4]
= -f'(6) – f'(4)
= -(-4)(5) … [From the table]
= 20.

(iv) If S(x) = g[g(x)] find S’ (6)
Solution:
S(x) = g[g(x)]

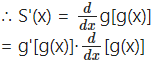
= g'[g(x)]∙g'(x)
∴ S ‘(6) = g'[g'(6)]∙g'(6)
= g'(2)∙g'(6) … [∵ g (x) = 2, when x = 6]
= 4 × 7 … [From the table]
= 28.

Question 5.

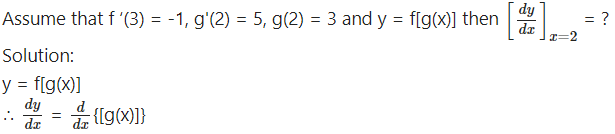
Question 6.

Solution:
Given f(1) = 4, g(1) = 3, f ‘(1) = 3, g'(1) = 4 …..(1)

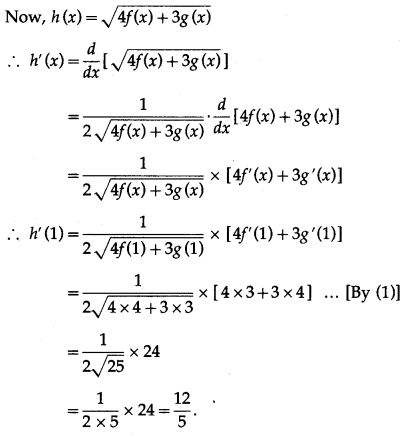
Question 7.
Find the x co-ordinates of all the points on the curve y = sin 2x – 2 sin x, 0 ≤ x < 2π where dy/dx= 0.
Solution:
y = sin 2x – 2 sin x, 0 ≤ x < 2π