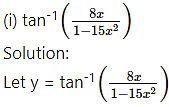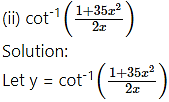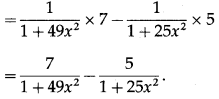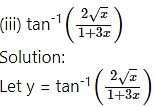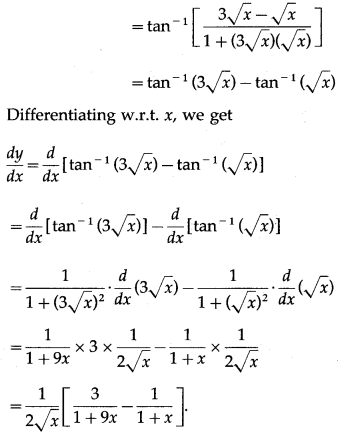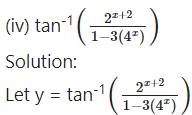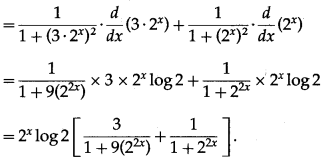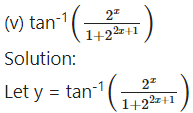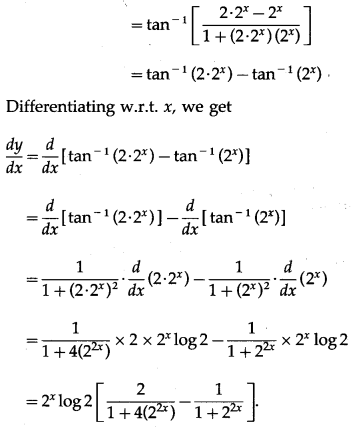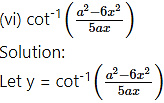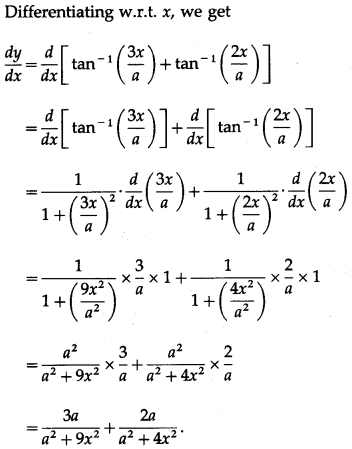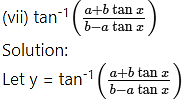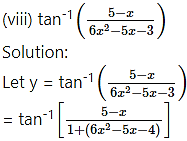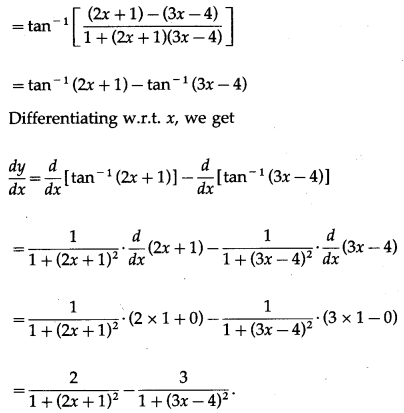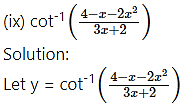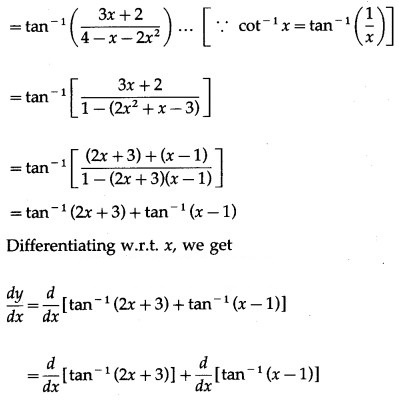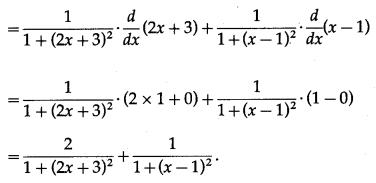Blog

Chapter 1 Differentiation Ex 1.2

Chapter 1 Differentiation Ex 1.2

Question 1.
Find the derivative of the function y = f (x) using the derivative of the inverse function x = ( y) in the following
(i) y = √x
Solution:
y = √x … (1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
 = x ∴ x = y²

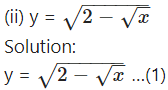
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),

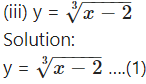
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),

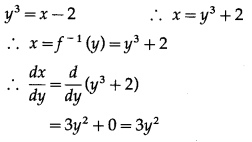
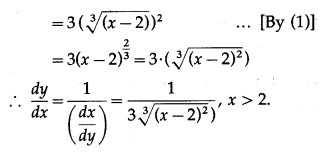
(iv) y = log (2x – 1)
Solution:
y = log (2x – 1) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),

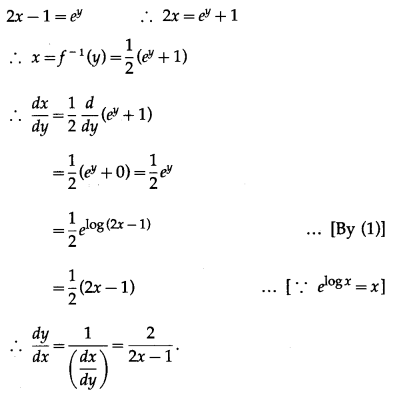
(v) y = 2x + 3
Solution:
y = 2x + 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),

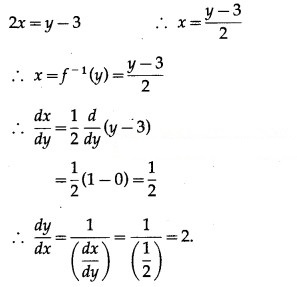
(vi) y =  – 3
Solution:
y =  – 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
 = y + 3
∴ x = log(y + 3)
∴ x = (y) = log(y + 3)

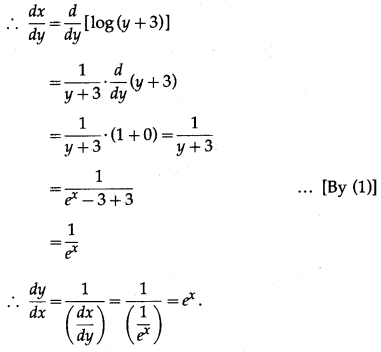
(vii) y =
Solution:
y =  ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
2x – 3 = log y ∴ 2x = log y + 3

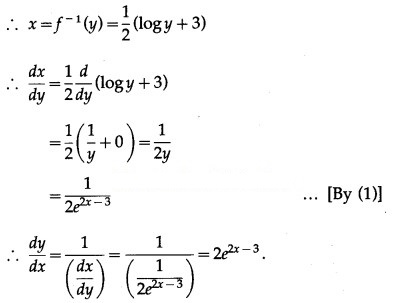
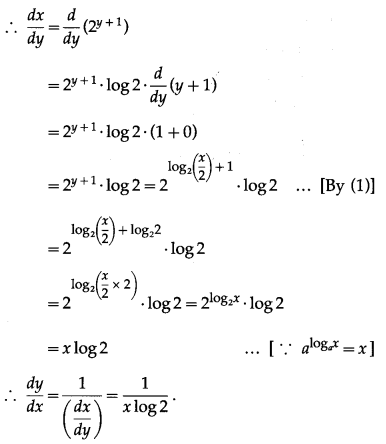
Question 2.
Find the derivative of the inverse function of
the following
(i) y =
Solution:
y =
Differentiating w.r.t. x, we get

(ii) y = x cos x
Solution:
y = x cos x
Differentiating w.r.t. x, we get

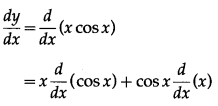
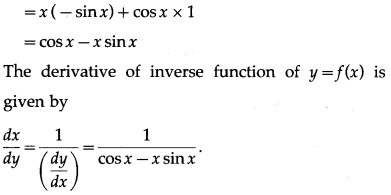
(iii) y = x·
Solution:
y = x·
Differentiating w.r.t. x, we get

(iv) y =  + logx
Solution:
y = + logx
Differentiating w.r.t. x, we get

(v) y = x logx
Solution:
y = x logx
Differentiating w.r.t. x, we get

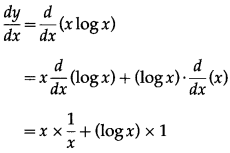
Question 3.
Find the derivative of the inverse of the following functions, and also fid their value at the points indicated against them.

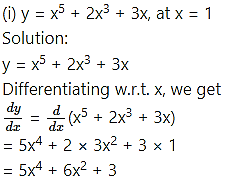
The derivative of inverse function of y = f(x) is given by

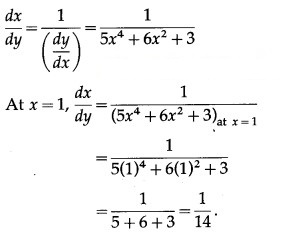
(ii) y =  + 3x + 2, at x = 0
Solution:
y =  + 3x + 2
Differentiating w.r.t. x, we get

The derivative of inverse function of y = f(x) is given by

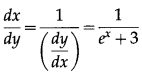
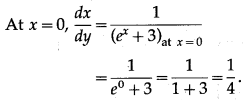
(iii) y = 3 + 2 log x³, at x = 1
Solution:
y = 3 + 2 log
= 3 + 6 log x
Differentiating w.r.t. x, we get

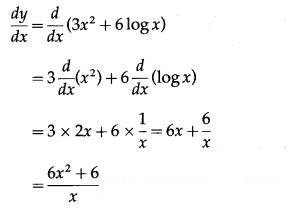
The derivative of inverse function of y = f(x) is given by

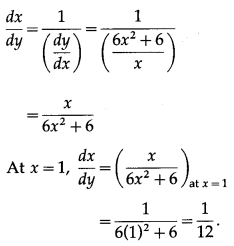
(iv) y = sin (x – 2) + , at x = 2
Solution:
y = sin (x – 2) +
Differentiating w.r.t. x, we get

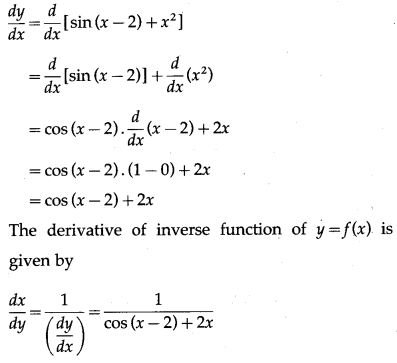
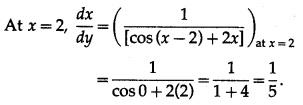
Question 4.
If f(x) =  + x – 2, find ()’ (0).
Question is modified.
If f(x) =  + x – 2, find ()’ (-2).
Solution:
f(x) =  + x – 2 ….(1)
Differentiating w.r.t. x, we get

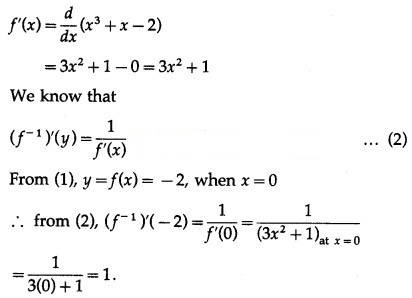
Question 5.
Using derivative prove

Solution:
let f(x) =
Differentiating w.r.t. x, we get

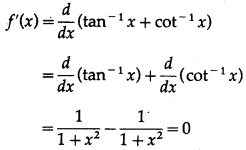
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k
Let x = 0.
Then f(0) = k ….(2)
From (1), f(0) =

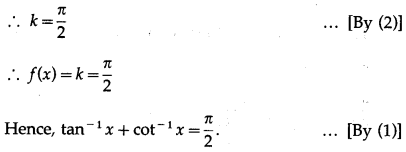
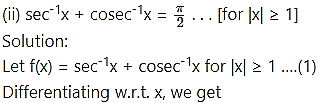
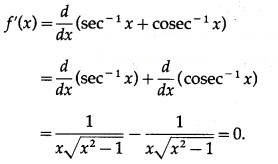
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k, where |x| > 1
Let x = 2.
Then, f(2) = k ……(2)

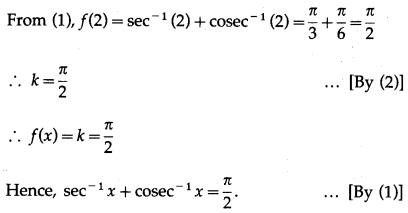
Question 6.
Diffrentiate the following w. r. t. x.
(i) ta(log x)
Solution:
Let y = ta (log x)
Differentiating w.r.t. x, we get

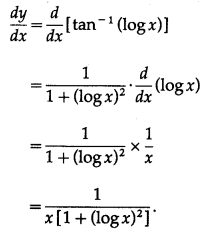
(ii)
Solution:
Let y =
Differentiating w.r.t. x, we get

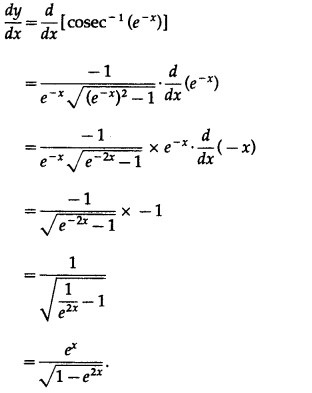
(iii)
Solution:
Let y =
Differentiating w.r.t. x, we get

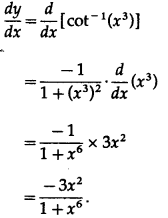
(iv)
Solution:
Let y =
Differentiating w.r.t. x, we get

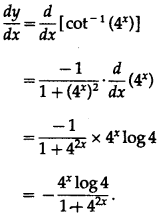
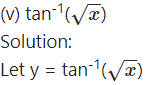
Differentiating w.r.t. x, we get

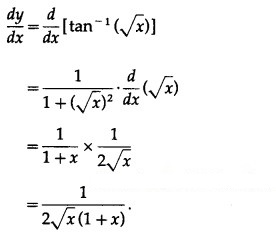
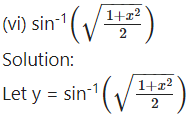
Differentiating w.r.t. x, we get

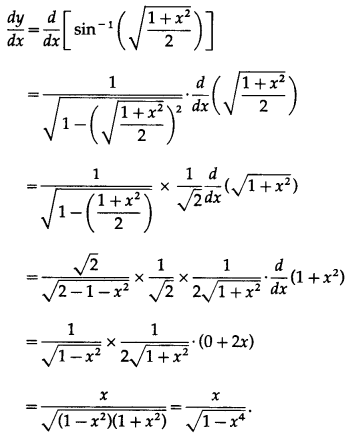
(vii)
Solution:
Let y =
Differentiating w.r.t. x, we get

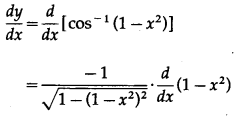
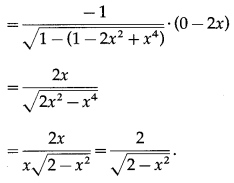
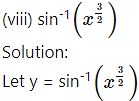
Differentiating w.r.t. x, we get

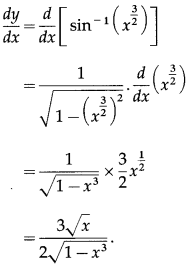
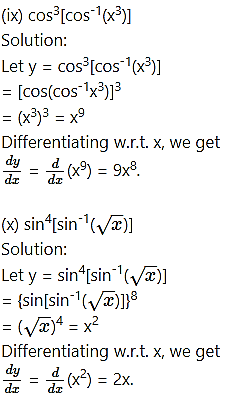
Question 7.

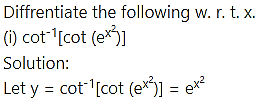
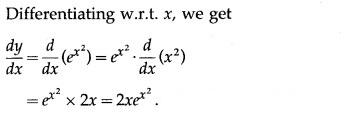
Solution:

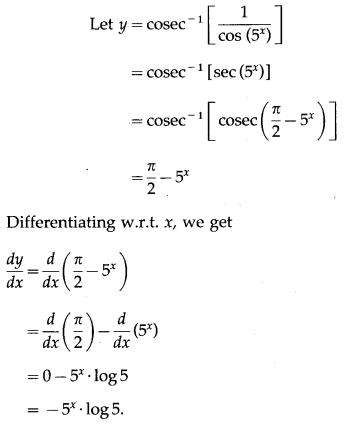
Solution:

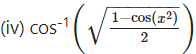
Solution:

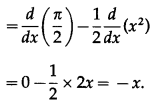
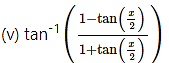
Solution:

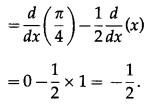
Solution:

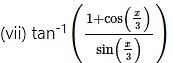
Solution:

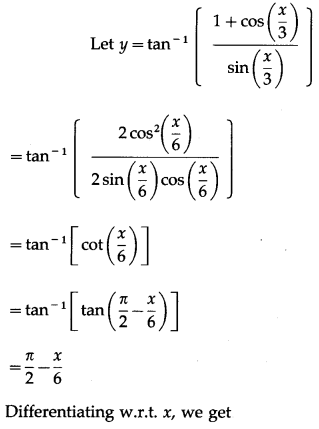
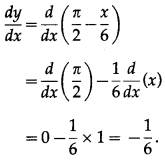
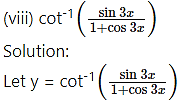
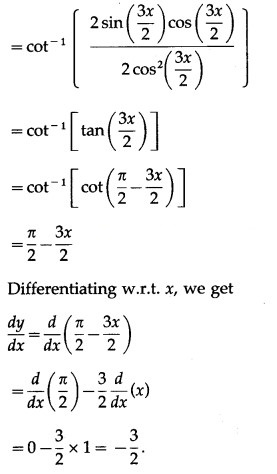
Solution:

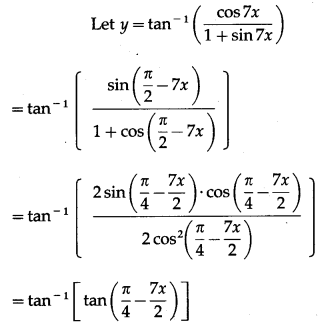
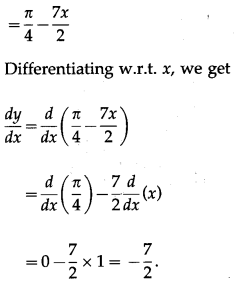
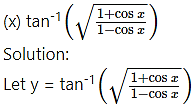
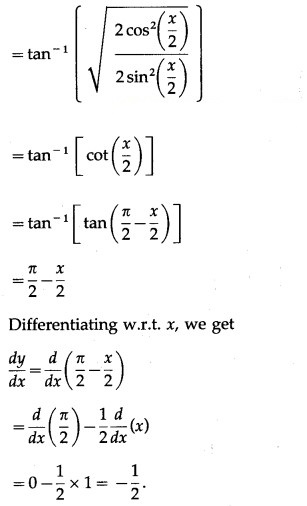
(xi) (cosec x + cot x)
Solution:
Let y = (cosec x + cot x)

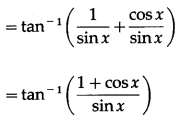
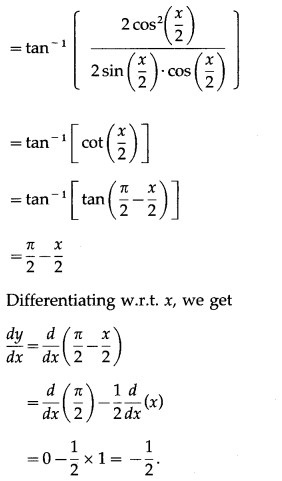
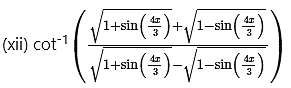
Solution:

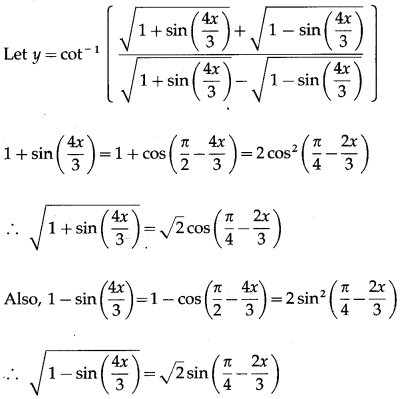
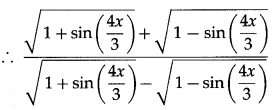
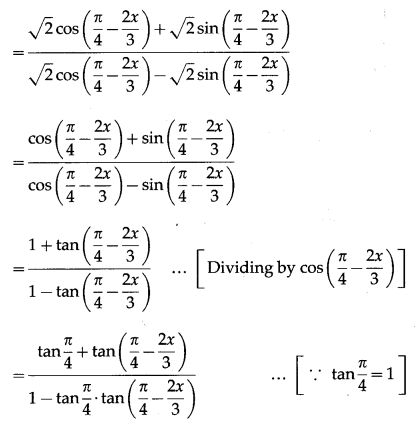
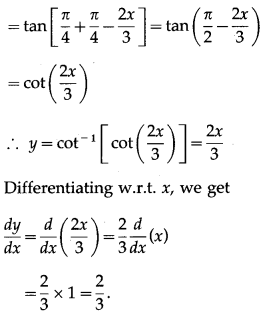
Question 8.
(i)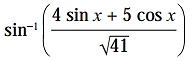 
Solution:

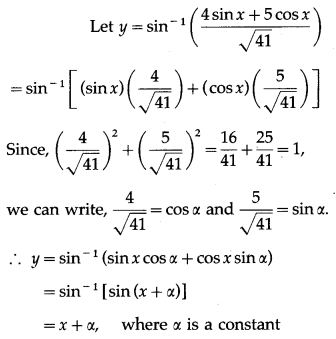
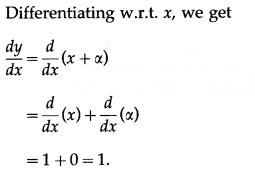
(ii)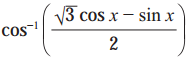 
Solution:

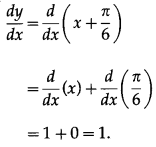
(iii)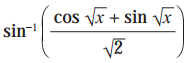 
Solution:

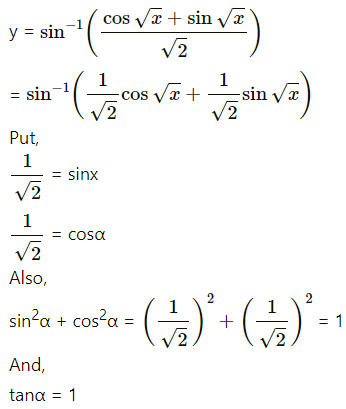
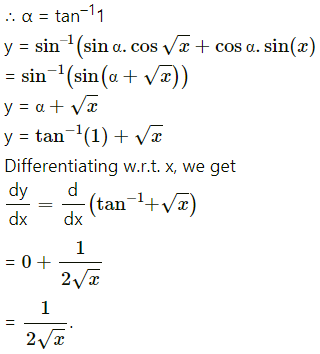
(iv)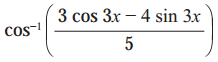 
Solution:

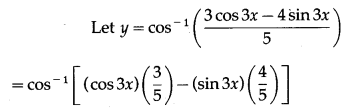
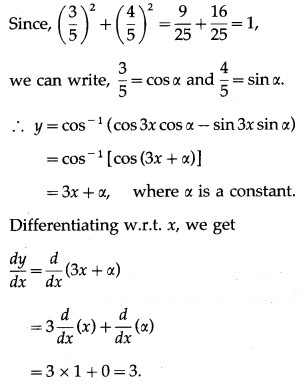
(v)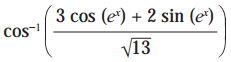 
Solution:


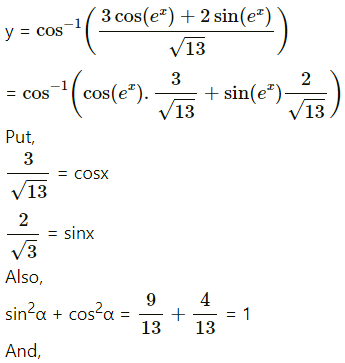
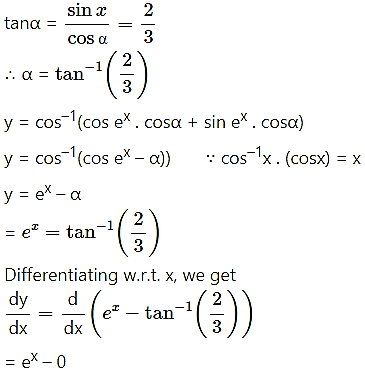
= e^x.

(vi)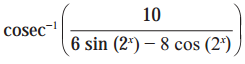 
Solution:

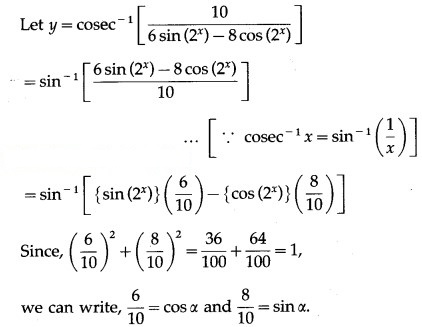
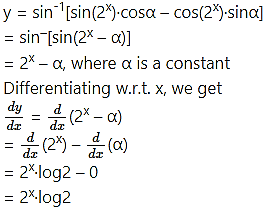
Question 9.
Diffrentiate the following w. r. t. x.

Solution:

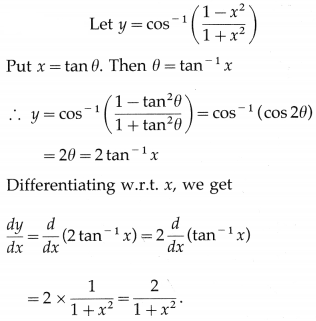
Solution:

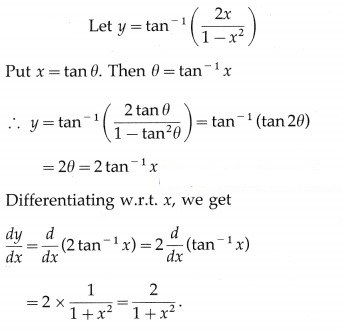
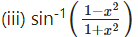
Solution: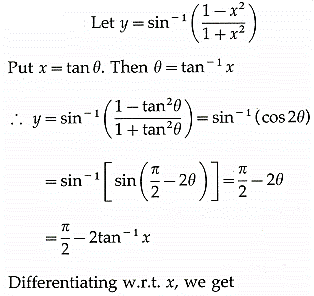

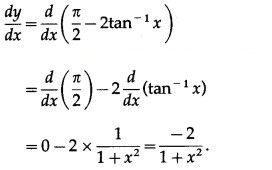
Solution:

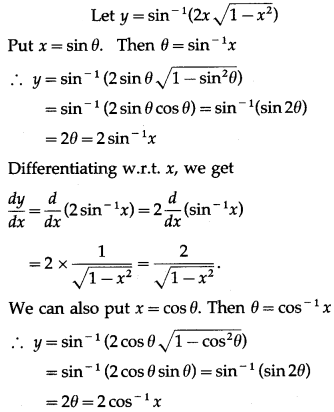
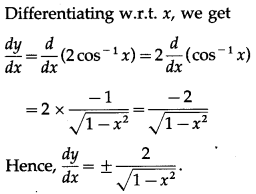
(v)

Solution:

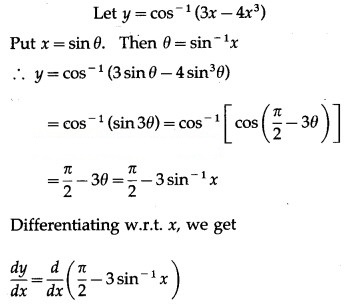
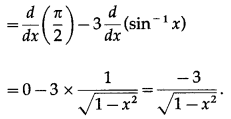
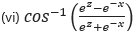
Solution: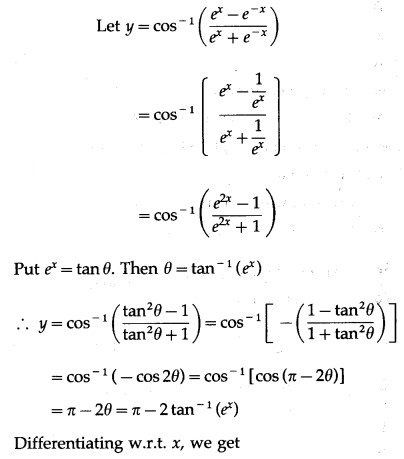

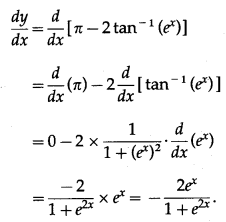
Solution:

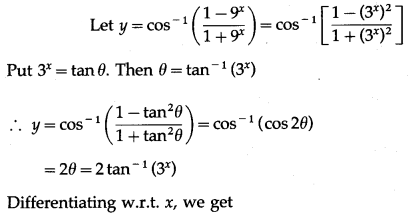
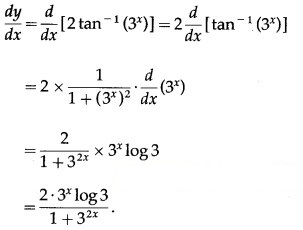
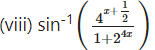
Solution:

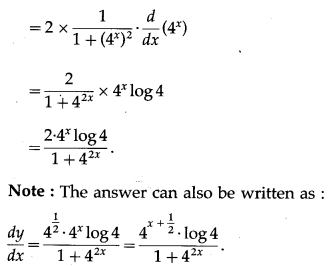
Solution:

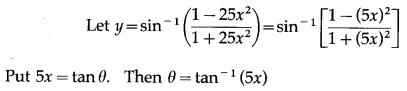
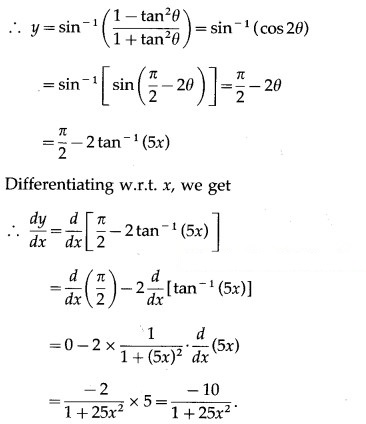
Solution:

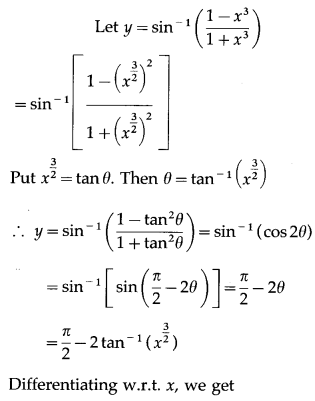
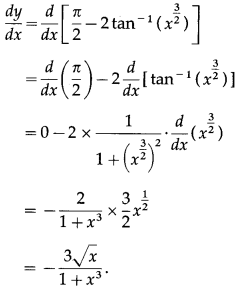
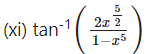
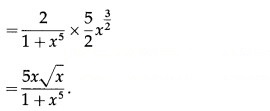
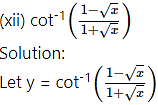
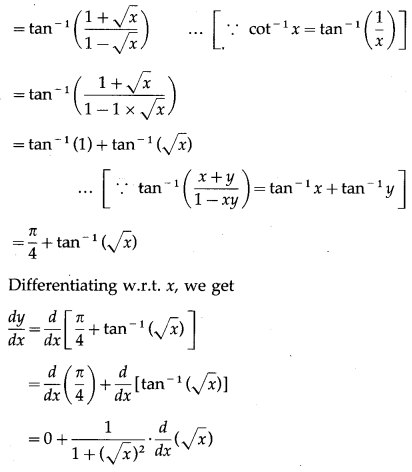
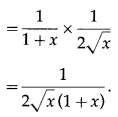
Question 10.
Diffrentiate the following w. r. t. x.