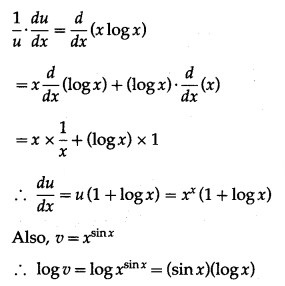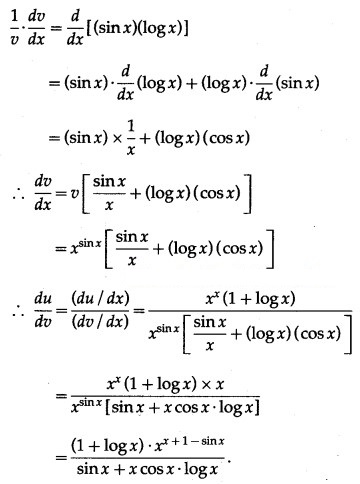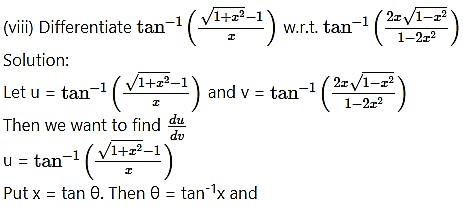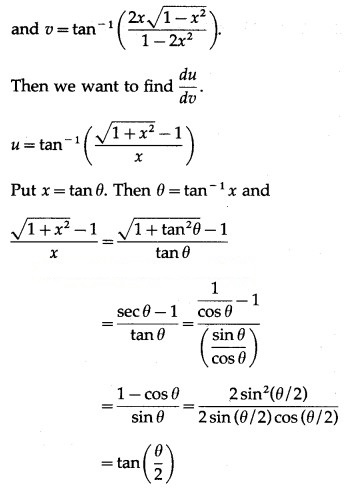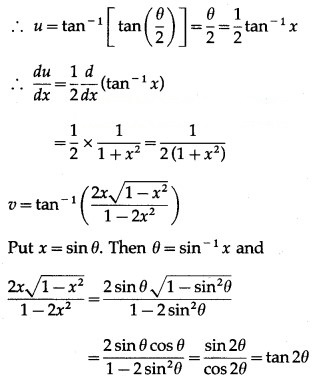Blog

Chapter 1 Differentiation Ex 1.4

Chapter 1 Differentiation Ex 1.4

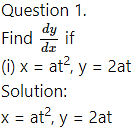
Differentiating x and y w.r.t. t, we get

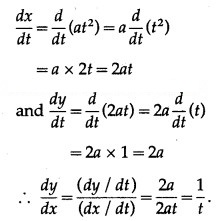
(ii) x = a cot θ, y = b cosec θ
Solution:
x = a cot θ, y = b cosec θ
Differentiating x and y w.r.t. θ, we get

(iv) x = sin θ, y = tan θ
Solution:
x = sin θ, y = tan θ
Differentiating x and y w.r.t. θ, we get

(v) x = a(1 – cos θ), y = b(θ – sin θ)
Solution:
x = a(1 – cos θ), y = b(θ – sin θ)
Differentiating x and y w.r.t. θ, we get

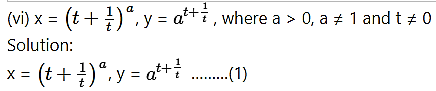
Differentiating x and y w.r.t. t, we get

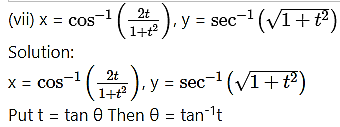
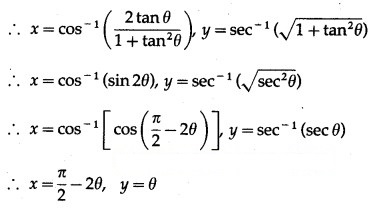
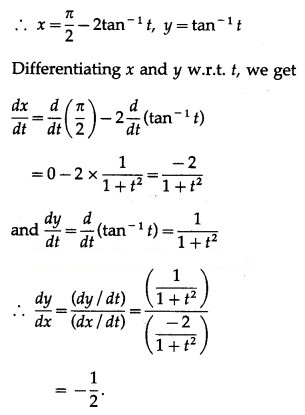
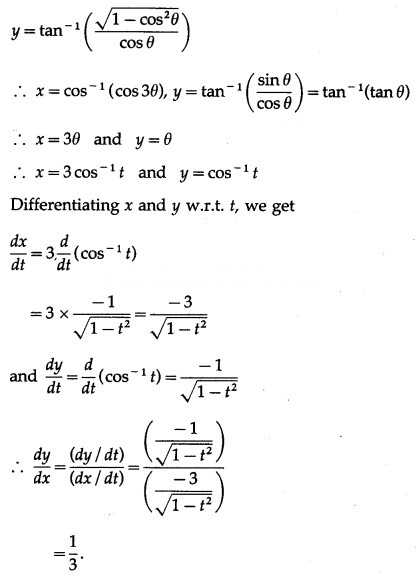
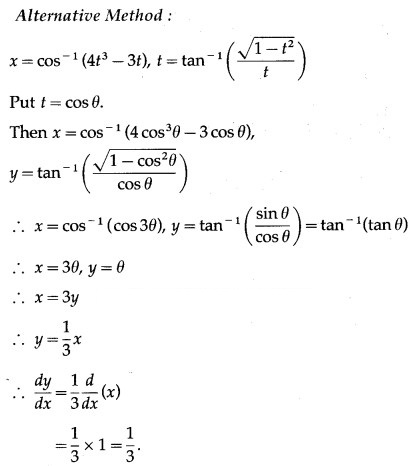
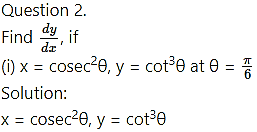
Differentiating x and y w.r.t. θ, we get

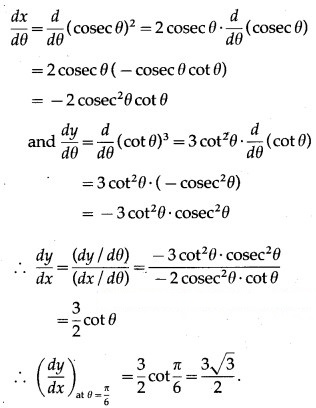
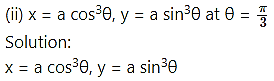
Differentiating x and y w.r.t. θ, we get

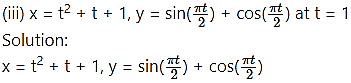
Differentiating x and y w.r.t. t, we get

(iv) x = 2 cos t + cos 2t, y = 2 sin t – sin 2t at t = 
Solution:
x = 2 cos t + cos 2t, y = 2 sin t – sin 2t
Differentiating x and y w.r.t. t, we get

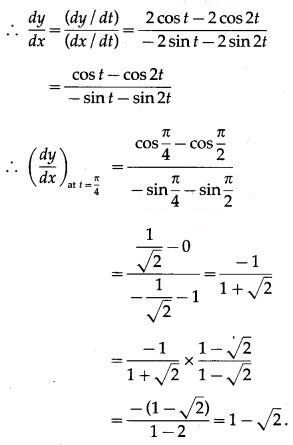
(v) x = t + 2 sin(πt), y = 3t – cos(πt) at t = 
Solution:
x = t + 2 sin(πt), y = 3t – cos(πt)
Differentiating x and y w.r.t. t, we get

Question 3.

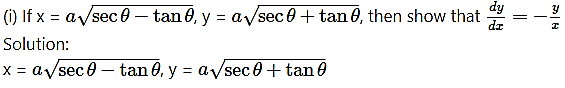
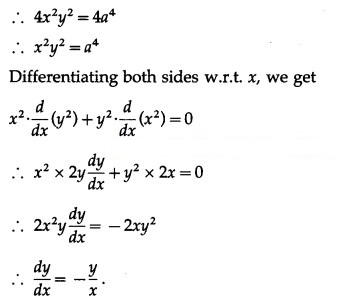
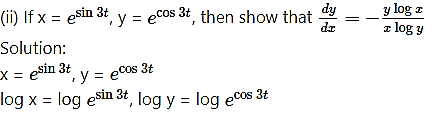
log x = (sin 3t)(log e), log y = (cos 3t)(log e)
log x = sin 3t, log y = cos 3t ….. (1) [∵ log e = 1]
Differentiating both sides w.r.t. t, we get

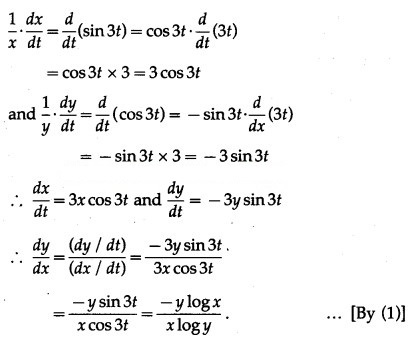
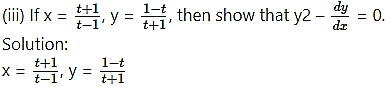
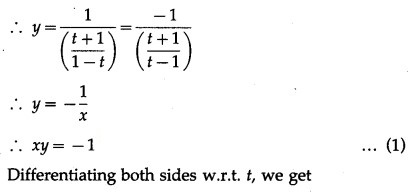
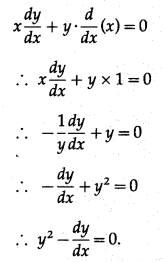
Differentiating x and y w.r.t. t, we get

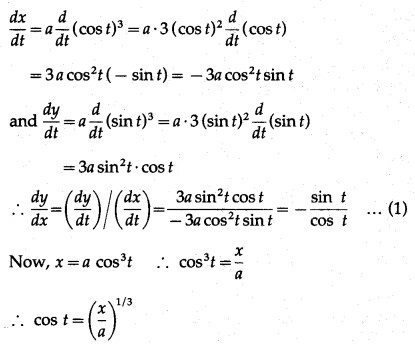
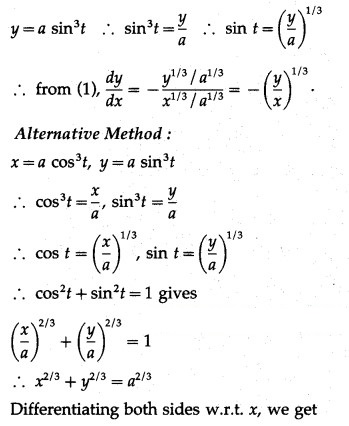
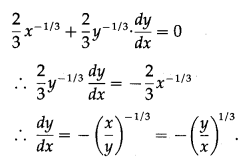
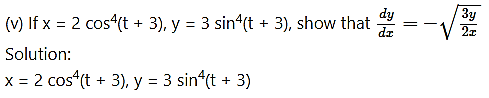
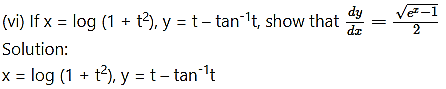
Differentiating x and y w.r.t. t, we get

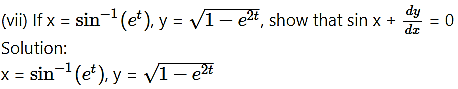
Differentiating x and y w.r.t. t, we get

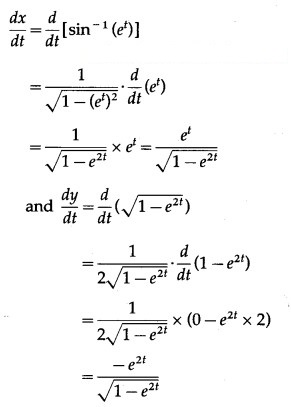
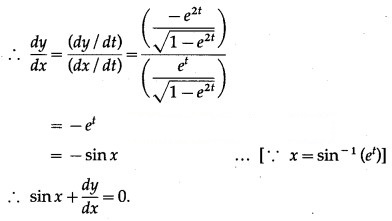
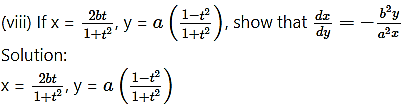
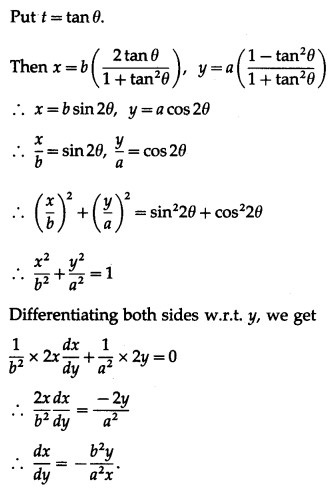
Question 4.
(i) Differentiate x sin x w.r.t tan x.
Solution:
Let u = x sinx and v = tan x
Then we want to find 
Differentiating u and v w.r.t. x, we get

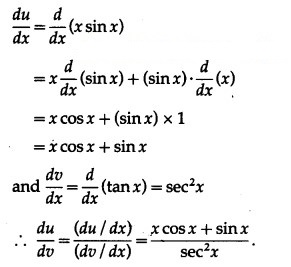
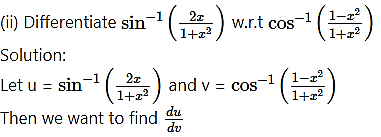
Solution:

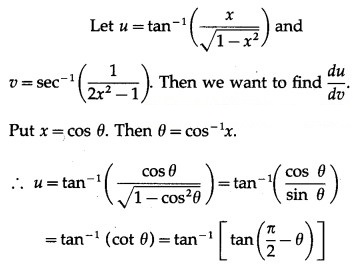
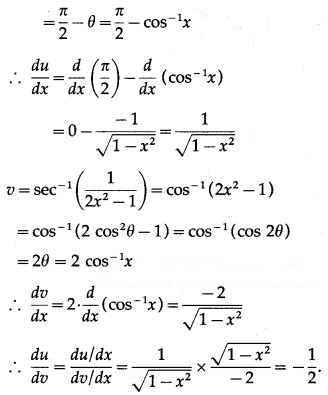
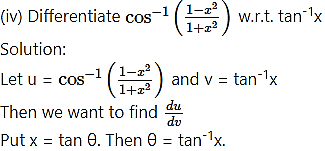
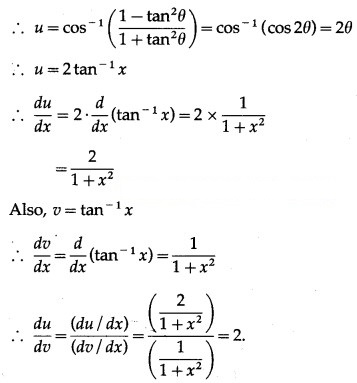
(v) Differentiate 3x w.r.t. log_x3.
Solution:

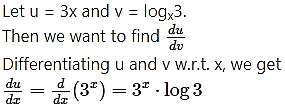
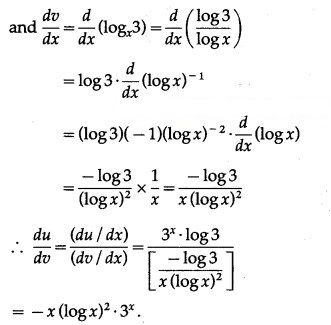
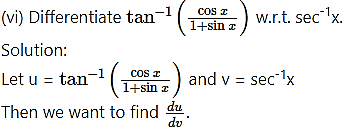
Differentiating u and v w.r.t. x, we get

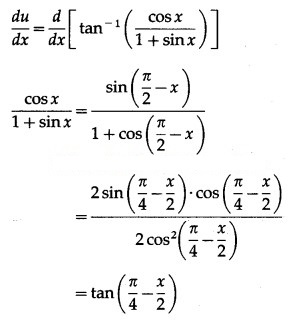
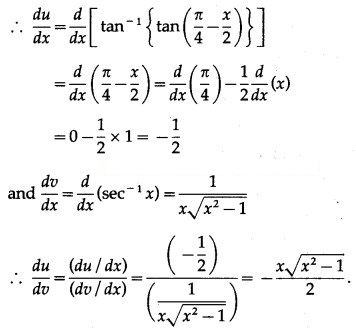
Differentiating both sides w.r.t. x, we get