Chapter 1 Linear Equations in Two Variables Set 1.4

Chapter 1 Linear Equations in Two Variables Set 1.4

Question 1.
Solve the following simultaneous equations.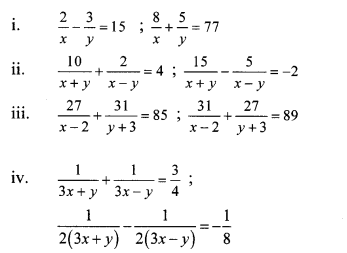

Solution:
i. The given simultaneous equations are

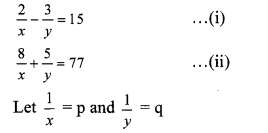
∴ Equations (i) and (ii) become
2p – 3q = 15 …(iii)
8p + 5q = 77 …(iv)
Multiplying equation (iii) by 4, we get
8p – 12q = 60 …(v)
Subtracting equation (v) from (iv), we get

ii. The given simultaneous equations are



Substituting x = 3 in equation (vi), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.

iii. The given simultaneous equations are

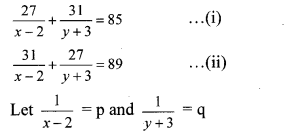
∴ Equations (i) and (ii) become
27p + 31q = 85 …(iii)
31p + 27q = 89 …(iv)
Adding equations (iii) and (iv), we get

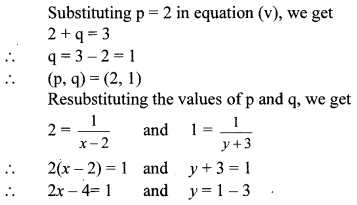
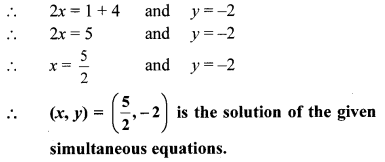
iv. The given simultaneous equations are


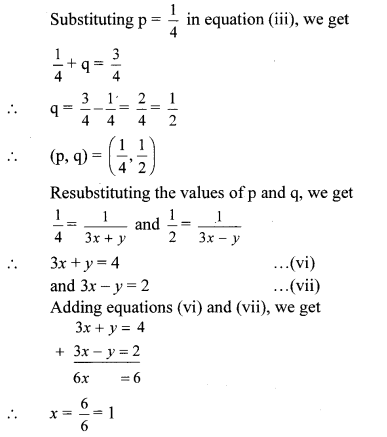
Substituting x = 1 in equation (vi), we get
3(1) + y = 4
∴ 3 + y = 4
∴ y = 4 – 3 = 1
∴ (x, y) = (1, 1) is the solution of the given simultaneous equations.

Question 1.
Complete the following table. (Textbook pg. no. 16)
Solution:

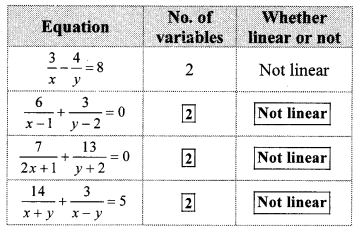
Question 2.
In the above table the equations are not linear. Can you convert the equations into linear equations? (Textbook pg. no. 17)
Answer:
Yes, the above given simultaneous equations can be converted to a pair of linear equations by making suitable substitutions.

Steps for solving equations reducible to a pair of linear equations.

• Step 1: Select suitable variables other than those which are in the equations.
• Step 2: Replace the given variables with new variables such that the given equations become linear equations in two variables.
• Step 3: Solve the new simultaneous equations and find the values of the new variables.
• Step 4: By resubstituting the value(s) of the new variables, find the replaced variables which are to be determined.

Question 3.
To solve given equations fill the below boxes suitably. (Text book pg.no. 19)
Answer:

Question 4.
The examples on textbook pg. no. 17 and 18 obtained by transformation are solved by elimination method. If you solve these equations by graphical method and by Cramer’s rule will you get the same answers? Solve and check it. (Textbook pg. no. 18)

Solution:

 
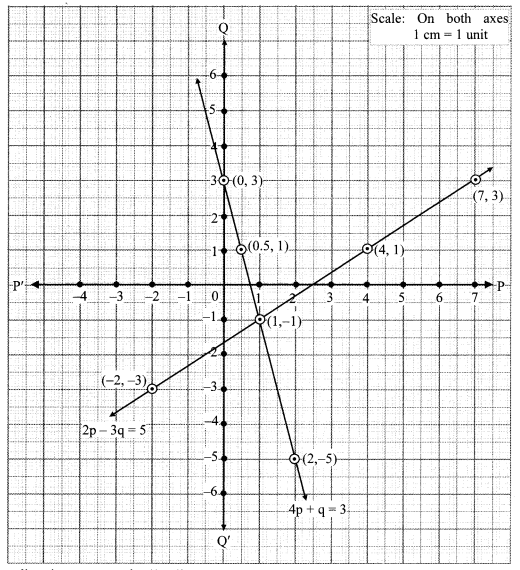
The two lines intersect at point (1,-1).
∴ p = 1 and q = -1 is the solution of the simultaneous equations 4p + q = 3 and 2p – 3q = 5.
Re substituting the values of p and q, we get

The two lines intersect at point (0, -1).
∴ x = 0 and y = -1 is the solution of the simultaneous equations x – y = 1 and x + y = -1.
∴ (x, y) = (0, -1) is the solution of the given simultaneous equations.