Chapter 1 Mathematical Logic Miscellaneous Exercise 1
Chapter 1 Mathematical Logic Miscellaneous Exercise 1
Question 1.
Select and write the correct answer from the given alternatives in each of the following questions :
i) If p ∧ q is false and p ∨ q is true, the ________ is not true.
(A) p ∨ q
(B) p ↔ q
(C) ~p ∨ ~q
(D) q ∨ ~p
Solution:
(b) p ↔ q.
(ii) (p ∧ q) → r is logically equivalent to ________.
(A) p → (q → r)
(B) (p ∧ q) → ~r
(C) (~p ∨ ~q) → ~r
(D) (p ∨ q) → r
Solution:
(a) p → (q → r) [Hint: Use truth table.]
(iii) Inverse of statement pattern (p ∨ q) → (p ∧ q) is ________.
(A) (p ∧ q) → (p ∨ q)
(B) ~(p ∨ q) → (p ∧ q)
(C) (~p ∧ ~q) → (~p ∨ ~q)
(D) (~p ∨ ~q) → (~p ∧ ~q)
Solution:
(c) (~p ∧ ~q) → (~p ∨ ~ q)
(iv) If p ∧ q is F, p → q is F then the truth values of p and q are ________.
(A) T, T
(B) T, F
(C) F, T
(D) F, F
Solution:
(b) T, F
(v) The negation of inverse of ~p → q is ________.
(A) q ∧ p
(B) ~p ∧ ~q
(C) p ∧ q
(D) ~q → ~p
Solution:
(a) q ∧ p
(vi) The negation of p ∧ (q → r) is ________.
(A) ~p ∧ (~q → ~r)
(B) p ∨ (~q ∨ r)
(C) ~p ∧ (~q → ~r)
(D) ~p ∨ (~q ∧ ~r)
Solution:
(d) ~p ∨ (q ∧ ~r)
(vii) If A = {1, 2, 3, 4, 5} then which of the following is not true?
(A) Ǝ x ∈ A such that x + 3 = 8
(B) Ǝ x ∈ A such that x + 2 < 9
(C) Ɐ x ∈ A, x + 6 ≥ 9
(D) Ǝ x ∈ A such that x + 6 < 10
Solution:
(c) Ǝ x ∈ A, x + 6 ≥ 9.
Question 2.
Which of the following sentences are statements in logic? Justify. Write down the truth
value of the statements :
(i) 4! = 24.
Solution:
It is a statement which is true, hence its truth value is ‘T’.
(ii) π is an irrational number.
Solution:
It is a statement which is true, hence its truth value is ‘T’.
(iii) India is a country and Himalayas is a river.
Solution:
It is a statement which is false, hence its truth value is ‘F’. ….[T ∧ F ≡ F]
(iv) Please get me a glass of water.
Solution:
It is an imperative sentence, hence it is not a statement.
(v) cos2θ – sin2θ = cos2θ for all θ ∈ R.
Solution:
It is a statement which is true, hence its truth value is ‘T’.
(vi) If x is a whole number the x + 6 = 0.
Solution:
It is a statement which is false, hence its truth value is ‘F’.
Question 3.
Write the truth values of the following statements :
(i) √5 is an irrational but 3√5 is a complex number.
Solution:
Let p : √5 is an irrational.
q : 3√5 is a complex number.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F]
(ii) Ɐ n ∈ N, n2 + n is even number while n2 – n is an odd number.
Solution:
Let p : Ɐ n ∈ N, n2 + n is an even number.
q : Ɐ n ∈ N, n2 – n is an odd number.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. … [T ∧ F ≡ F].
(iii) Ǝ n ∈ N such that n + 5 > 10.
Solution:
Ǝ n ∈ N, such that n + 5 > 10 is a true statement, hence its truth value is T.
(All n ≥ 6, where n ∈ N, satisfy n + 5 > 10).
(iv) The square of any even number is odd or the cube of any odd number is odd.
Solution:
Let p : The square of any even number is odd.
q : The cube of any odd number is odd.
Then the symbolic form of the given statement is p ∨ q.
The truth values of p and q are F and T respectively.
∴ the truth value of p ∨ q is T. … [F ∨ T ≡ T].
(v) In ∆ ABC if all sides are equal then its all angles are equal.
Solution:
Let p : ABC is a triangle and all its sides are equal.
q : Its all angles are equal.
Then the symbolic form of the given statement is p → q
If the truth value of p is T, then the truth value of q is T.
∴ the truth value of p → q is T. … [T → T ≡ T].
(vi) Ɐ n ∈ N, n + 6 > 8.
Solution:
Ɐ n ∈ N, 11 + 6 > 8 is a false statement, hence its truth value is F.
{n = 1 ∈ N, n = 2 ∈ N do not satisfy n + 6 > 8).
Question 4.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of each of the following statement :
(i) Ǝ x ∈ A such that x + 8 = 15.
Solution:
True
(ii) Ɐ x ∈ A, x + 5 < 12.
Solution:
False
(iii) Ǝ x ∈ A, such that x + 7 ≥ 11.
Solution:
True
(iv) Ɐ x ∈ A, 3x ≤ 25.
Solution:
False
Question 5.
Write the negations of the following :
(i) Ɐ n ∈ A, n + 7 > 6.
Solution:
The negation of the given statements are :
Ǝ n ∈ A, such that n + 7 ≤ 6.
OR Ǝ n ∈ A, such that n + 7 ≯ 6.
(ii) Ǝ x ∈ A, such that x + 9 ≤ 15.
Solution:
Ɐ x ∈ A, x + 9 > 15.
(iii) Some triangles are equilateral triangle.
Solution:
All triangles are not equilateral triangles.
Question 6.
Construct the truth table for each of the following :
(i) p → (q → p)
Solution:
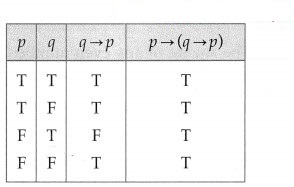
(ii) (~p ∨ ~q) ↔ [~(p ∧ q)]
Solution:
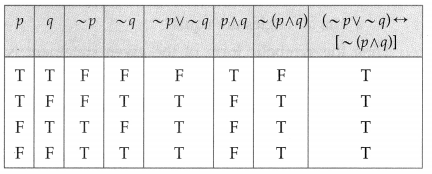
(iii) ~(~p ∧ ~q) ∨ q
Solution:
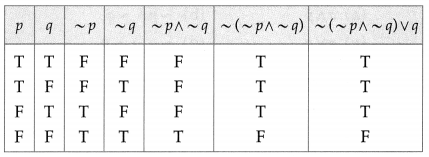
(iv) [(p ∧ q) ∨ r] ∧ [~r ∨ (p ∧ q)]
Solution:
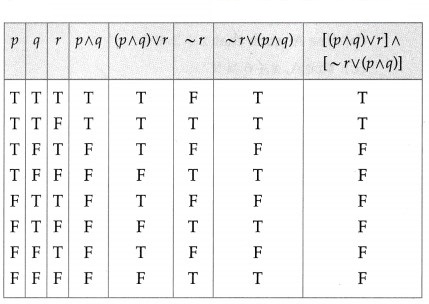
(v) [(~p ∨ q) ∧ (q → r)] → (p → r)
Solution:
Question 7.
Determine whether the following statement patterns are tautologies contradictions or contingencies :
(i) [(p → q) ∧ ~q)] → ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ [(p → q) ∧ ~q)] → ~p is a tautology.
(ii) [(p ∨ q) ∧ ~p] ∧ ~q
Solution:
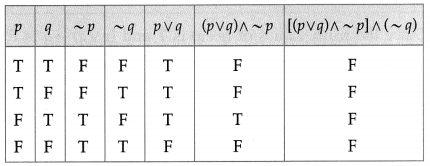
All the entries in the last column of the above truth table are F.
∴ [(p ∨ q) ∧ ~p] ∧ ~q is a contradiction.
(iii) (p → q) ∧ (p ∧ ~q)
Solution:
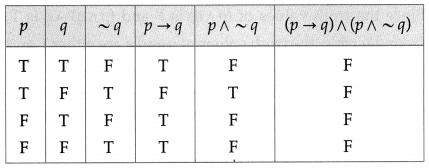
All the entries in the last column of the above truth table are F.
∴ (p → q) ∧ (p ∧ ~q) is a contradiction.
(iv) [p → (q → r)] ↔ [(p ∧ q) → r]
Solution:
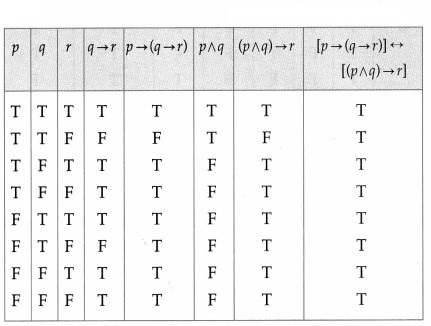
All the entries in the last column of the above truth table are T.
∴ [p → (q → r)] ↔ [(p ∧ q) → r] is a tautology.
(v) [(p ∧ (p → q)] → q
Solution:
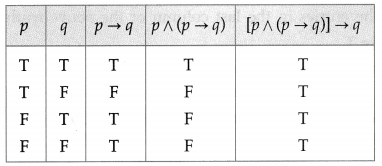
All the entries in the last column of the above truth table are T.
∴ [(p ∧ (p → q)] → q is a tautology.
(vi) (p ∧ q) ∨ (~p ∧ q) ∨ (p ∨ ~q) ∨ (~p ∧ ~q)
Solution: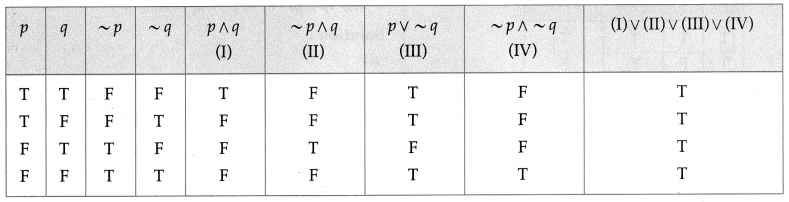
All the entries in the last column of the above truth table are T.
∴ (p ∧ q) ∨ (~p ∧ q) ∨ (p ∨ ~q) ∨ (~p ∧ ~q) is a tautology.
(vii) [(p ∨ ~q) ∨ (~p ∧ q)] ∧ r
Solution:
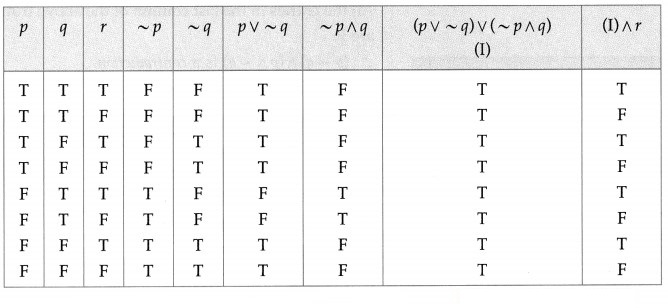
The entries in the last column are neither T nor all F.
∴ [(p ∨ ~q) ∨ (~p ∧ q)] ∧ r is a contingency.
(viii) (p → q) ∨ (q → p)
Solution:
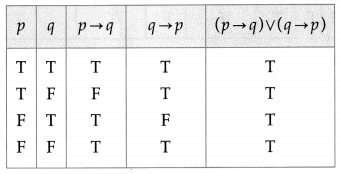
All the entries in the last column of the above truth table are T.
∴ (p → q) ∨ (q → p) is a tautology.
Question 8.
Determine the truth values ofp and q in the following cases :
(i) (p ∨ q) is T and (p ∧ q) is T
Solution:
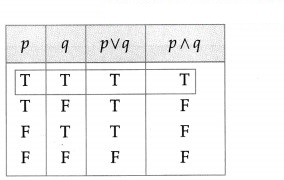
Since p ∨ q and p ∧ q both are T, from the table the truth values of both p and q are T.
(ii) (p ∨ q) is T and (p ∨ q) → q is F
Solution:
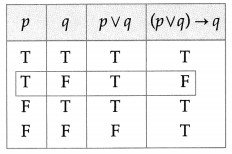
Since the truth values of (p ∨ q) is T and (p ∨ q) → q is F, from the table, the truth values of p and q are T and F respectively.
(iii) (p ∧ q) is F and (p ∧ q) → q is T
Solution:
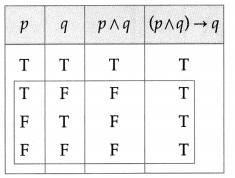
Since the truth values of (p ∧ q) is F and (p ∧ q) → q is T, from the table, the truth values of p and q are either T and F respectively or F and T respectively or both F.
Question 9.
Using truth tables prove the following logical equivalences :
(i) p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Solution:
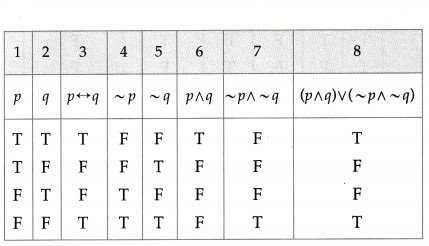
The entries in the columns 3 and 8 are identical.
∴ p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q).
(ii) (p ∧ q) → r ≡ p → (q → r)
Solution:
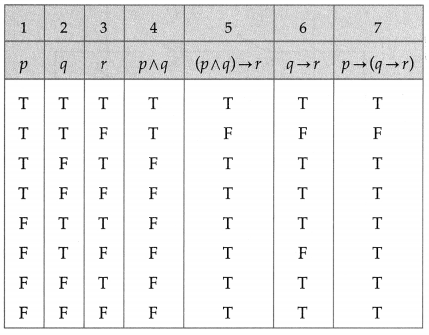
The entries in the columns 5 and 7 are identical.
∴ (p ∧ q) → r ≡ p → (q → r).
Question 10.
Using rules in logic, prove the following :
(i) p ↔ q ≡ ~ (p ∧ ~q) ∧ ~(q ∧ ~p)
Solution:
By the rules of negation of biconditional,
~(p ↔ q) ≡ (p ∧ ~q) ∨ (q ∧ ~p)
∴ ~ [(p ∧ ~ q) ∨ (q ∧ ~p)] ≡ p ↔ q
∴ ~(p ∧ ~q) ∧ ~(q ∧ ~p) ≡ p ↔ q … (Negation of disjunction)
≡ p ↔ q ≡ ~(p ∧ ~ q) ∧ ~ (q ∧ ~p).
(ii) ~p ∧ q ≡ (p ∨ q) ∧ ~p
Solution:
(p ∨ q) ∧ ~ p
≡ (p ∧ ~p) ∨ (q ∧ ~p) … (Distributive Law)
≡ F ∨ (q ∧ ~p) … (Complement Law)
≡ q ∧ ~ p … (Identity Law)
≡ ~p ∧ q …(Commutative Law)
∴ ~p ∧ q ≡ (p ∨ q) ∧ ~p.
(iii) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:
~ (p ∨ q) ∨ (~p ∧ q)
≡ (~p ∧ ~q) ∨ (~p ∧ q) … (Negation of disjunction)
≡ ~p ∧ (~q ∨ q) … (Distributive Law)
≡ ~ p ∧ T … (Complement Law)
≡ ~ p … (Identity Law)
∴ ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p.
Question 11.
Using the rules in logic, write the negations of the following :
(i) (p ∨ q) ∧ (q ∨ ~r)
Solution:
The negation of (p ∨ q) ∧ (q ∨ ~ r) is
~ [(p ∨ q) ∧ (q ∨ ~r)]
≡ ~ (p ∨ q) ∨ ~ (q ∨ ~r) … (Negation of conjunction)
≡ (~p ∧ ~q) ∨ [~q ∧ ~(~r)] … (Negation of disjunction)
≡ {~ p ∧ ~q) ∨ (~q ∧ r) … (Negation of negation)
≡ (~q ∧ ~p) ∨ (~q ∧ r) … (Commutative law)
≡ (~ q) ∧ (~ p ∨ r) … (Distributive Law)
(ii) p ∧ (q ∨ r)
Solution:
The negation of p ∧ (q ∨ r) is
~ [p ∧ (q ∨ r)]
≡ ~ p ∨ ~(q ∨ r) … (Negation of conjunction)
≡ ~p ∨ (~q ∧ ~r) … (Negation of disjunction)
(iii) (p → q) ∧ r
Solution:
The negation of (p → q) ∧ r is
~ [(p → q) ∧ r]
≡ ~ (p → q) ∨ (~ r) … (Negation of conjunction)
≡ (p ∧ ~q) ∨ (~ r) … (Negation of implication)
(iv) (~p ∧ q) ∨ (p ∧ ~q)
Solution:
The negation of (~ p ∧ q) ∨ (p ∧ ~ q) is
~ [(~p ∧ q) ∨ (p ∧ ~q)]
≡ ~(~p ∧ q) ∧ ~ (p ∧ ~q) … (Negation of disjunction)
≡ [~(~p) ∨ ~q] ∧ [~p ∨ ~(q)] … (Negation of conjunction)
≡ (p ∨ ~ q) ∧ (~ p ∨ q) … (Negation of negation)
Question 12.
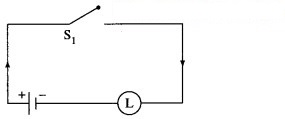
Express the following circuits in the symbolic form. Prepare the switching table :
(i)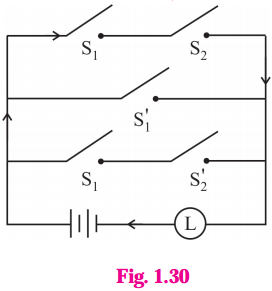
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
~ p : the switch S1‘ is closed or the switch S1 is open
~ q: the switch S2‘ is closed or the switch S2 is open.
Then the symbolic form of the given circuit is :
(p ∧ q) ∨ (~p) ∨ (p ∧ ~q).
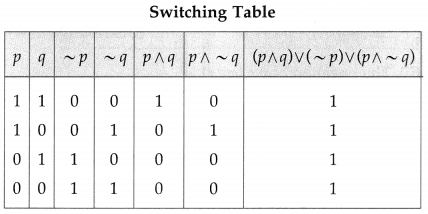
(ii)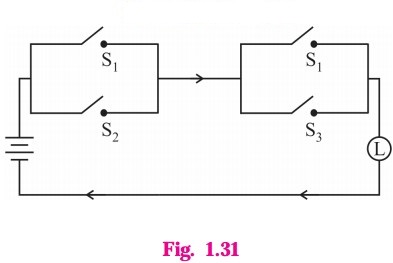
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
r : the switch S3 is closed.
Then the symbolic form of the given statement is : (p ∨ q) ∧ (p ∨ r).
Question 13.
Simplify the following so that the new circuit has minimum number of switches. Also, draw the simplified circuit.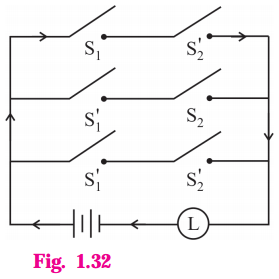
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
~ p: the switch S1‘ is closed or the switch S1 is open
~ q: the switch S2‘ is closed or the switch S2 is open.
Then the given circuit in symbolic form is :
(p ∧ ~q) ∨ (~p ∧ q) ∨ (~p ∧ ~q)
Using the laws of logic, we have,
(p ∧ ~q) ∨ (~p ∧ q) ∨ (~p ∧ ~ q)
= (p ∧ ~q) ∨ [(~p ∧ q) ∨ (~p ∧ ~q) …(By Complement Law)
= (p ∧ ~q) ∨ [~p ∧ (q ∨ ~q)} (By Distributive Law)
= (p ∧ ~q) ∨ (~p ∧ T) …(By Complement Law)
= (p ∧ ~q) ∨ ~ p …(By Identity Law)
= (p ∨ ~p) ∧ (~q ∨ ~p) …(By Distributive Law)
= ~q ∨ ~p …(By Identity Law)
= ~p ∨ ~p …(By Commutative Law)
Hence, the simplified circuit for the given circuit is :
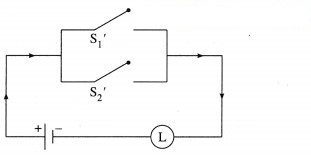
(ii)
Solution:
(ii) Let p : the switch S1 is closed
q : the switch S2 is closed
r : the switch S3 is closed
s : the switch S4 is closed
t : the switch S5 is closed
~ p : the switch S1‘ is closed or the switch S1 is open
~ q : the switch S2‘ is closed or the switch S2 is open
~ r : the switch S3‘ is closed or the switch S3 is open
~ s : the switch S4‘ is closed or the switch S4 is open
~ t : the switch S5‘ is closed or the switch S5 is open.
Then the given circuit in symbolic form is
[(p ∧ q) ∨ ~r ∨ ~s ∨ ~t] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)]
Using the laws of logic, we have,
[(p ∧ q) ∨ ~r ∨ ~s ∨ ~ t] ∧ [(p A q) ∨ (r ∧ s ∧ t)]
= [(p∧ q) ∨ ~(r ∧ s ∧ t)] ∧ [(p ∧ q) ∨ (r ∧ s ∧ t)] … (By De Morgan’s Law)
= (p ∧ q) ∨ [ ~(r ∧ s ∧ t) ∧ (r ∧ s ∧ t)] … (By Distributive Law)
= (p ∧ q) ∨ F … (By Complement Law)
= p ∧ q … (By Identity Law)
Hence, the alternative simplified circuit is :
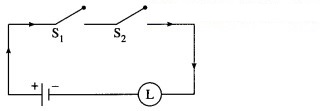
Question 14.
Check whether the following switching circuits are logically equivalent – Justify.
(A)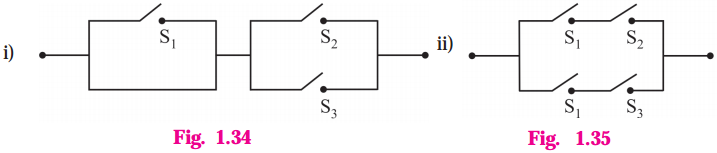
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
r : the switch S3 is closed
(A) The symbolic form of the given switching circuits are
p ∧ (q ∨ r) and (p ∧ q) ∨ (p ∧ r) respectively.
By Distributive Law, p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Hence, the given switching circuits are logically equivalent.
(B)
Solution:
The symbolic form of the given switching circuits are
(p ∨ q) ∧ (p ∨ r) and p ∨ (q ∧ r)
By Distributive Law,
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Hence, the given switching circuits are logically equivalent.
Question 15.
Give alternative arrangement of the switching following circuit, has minimum switches.
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
r : the switch S3 is closed
~p : the switch S1‘ is closed, or the switch S1 is open
~q : the switch S2‘ is closed or the switch S2 is open.
Then the symbolic form Of the given circuit is :
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r)
Using the laws of logic, we have,
(p ∧ q ∧ ~p) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r)
≡ (p ∧ ~p ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) y (p ∧ ~q ∧ r) …(By Commutative Law)
≡ (F ∧ q) ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Complement Law)
≡ F ∨ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ (~p ∧ q ∧ r) ∨ (p ∧ q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ [(~p ∨ p) ∧ (q ∧ r)] ∨ (p ∧ ~q ∧ r) … (By Distributive Law)
≡ [T ∧ (q ∧ r)] ∨ (p ∧ ~q ∧ r) = (q ∧ r) ∨ (p ∧ ~q ∧ r) …(By Complement Law)
≡ (q ∧ r) ∨ (p ∧ ~q ∧ r) … (By Identity Law)
≡ [q ∨ (p ∧ ~q)] ∧ r … (By Distributive Law)
≡ [q ∨ p) ∧ ((q ∨ ~q)] ∧ r … (By Distributive Law)
≡ [(q ∨ p) ∧ T] ∧ r …(By Complement Law)
≡ (q ∨ p) ∧ r … (By Identity Law)
≡ (p ∨ q) ∧ r …(By Commutative Law)
∴ the alternative arrangement of the new circuit with minimum switches is :
Question 16.
Simplify the following so that the new circuit circuit.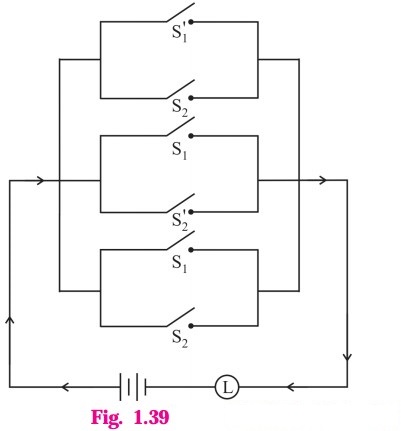
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
~ p : the switch S1‘ is closed or the switch S1 is open
~ q : the switch S2‘ is closed or the switch S2 is open.
Then the symbolic form of the given switching circuit is :
(~p ∨ q) ∨ (p ∨ ~q) ∨ (p ∨ q)
Using the laws of logic, we have,
(~p ∨ q) ∨ (p ∨ ~q) ∨ (p ∨ q)
≡ (~p ∨ q ∨ p ∨ ~q) ∨ (p ∨ q)
≡ [(~p ∨ p) ∨ (q ∨ ~q)] ∨ (p ∨ q) … (By Commutative Law)
≡ (T ∨ T) ∨ (p ∨ q) … (By Complement Law)
≡ T ∨ (p ∨ q) … (By Identity Law)
≡ T … (By Identity Law)
∴ the current always flows whether the switches are open or closed. So, it is not necessary to use any switch in the circuit.
∴ the simplified form of given circuit is :

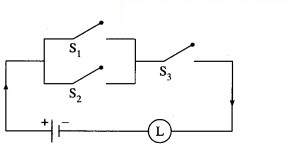
Question 17.
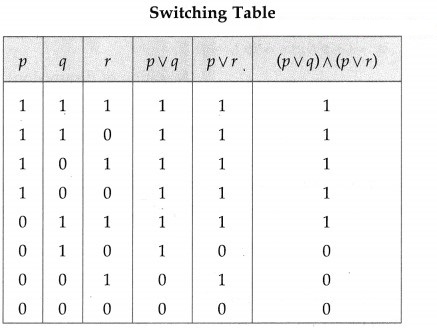
Represent the following switching circuit in symbolic form and construct its switching table. Write your conclusion from the switching table.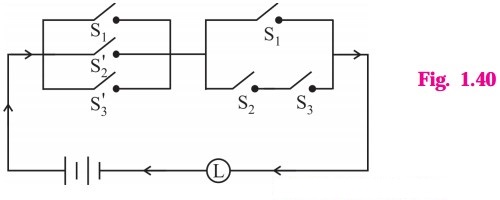
Solution:
Let p : the switch S1 is closed
q : the switch S2 is closed
r : the switch S3 is closed
~ q : the switch S2‘ is closed or the switch S2 is open
~ r : the switch S3‘ is closed or the switch S3 is open.
Then, the symbolic form of the given switching circuit is : [p ∨ (~ q) ∨ (~ r)] ∧ [p ∨ (q ∧ r)]
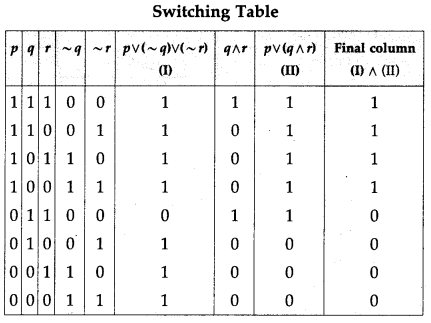
From the table, the’ final column’ and the column of p are identical. Hence, the given circuit is equivalent to the simple circuit with only one switch S1.
the simplified form of the given circuit is :