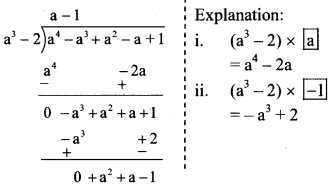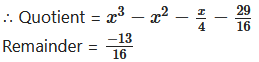Chapter 10 Division of Polynomials Set 10.2
Division of Polynomials Class 8 Practice Set 10.2 Question 1. Divide and write the quotient and the remainder.
i. (y2 + 10y + 24) ÷ (y + 4)
ii. (p2 + 7p – 5) ÷ (p + 3)
iii. (3x + 2x2 + 4x3) ÷ (x – 4)
iv. (2m3 + m2 + m + 9) ÷ (2m – 1)
v. (3x – 3x2 – 12 + x4 + x3) ÷ (2 + x2)
vi. (a4 – a3 + a2 – a + 1) ÷ (a3 – 2)
vii. (4x4 – 5x3 – 7x + 1) ÷ (4x – 1)
Solution:
i. (y2 + 10y + 24) ÷ (y + 4)
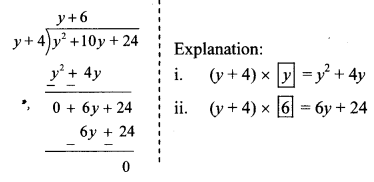
∴ Quotient = y + 6
Remainder = 0
ii. (p2 + 7p – 5) ÷ (p + 3)

∴ Quotient = p + 4
Remainder = -17
iii. (3x + 2x2 + 4x3) ÷ (x – 4)
Write the dividend in descending order of their indices.
3x + 2x² + 4x³ = 4x³ + 2x² + 3x

∴ Quotient = 4x² + 18x + 75
Remainder = 300
iv. (2m3 + m2 + m + 9) ÷ (2m – 1)

∴ Quotient = m² + m + 1
Remainder = 10
v. (3x – 3x2 – 12 + x4 + x3) ÷ (2 + x2)
Write the dividend in descending order of their indices.
(x4 + x3 – 3x2 + 3x – 12) ÷ (x2 + 2)

∴ Quotient = x² + x – 5
Remainder = x – 2
vi. (a4 – a3 + a2 – a + 1) ÷ (a3 – 2)
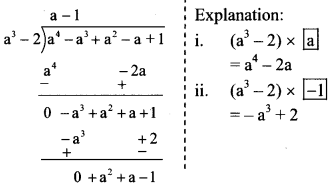
∴ Quotient = a – 1
Remainder = a² + a – 1
vii. (4x4 – 5x3 – 7x + 1) ÷ (4x – 1)
Write the dividend in descending order of their indices.
(4x4 – 5x3 – 7x + 1) = (4x4 – 5x3 + 0x2 – 7x + 1)