Chapter 12 Equations in One Variable 12.2
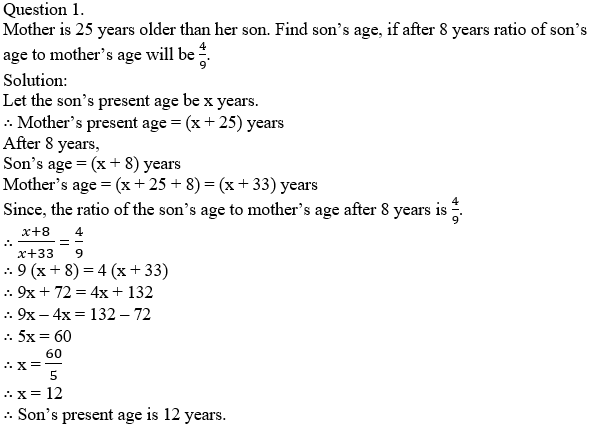

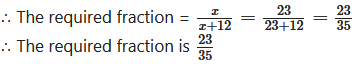
Question 3.
The ratio of the weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Let the weight of zinc in the brass utensil be x gm.
Since, the ratio of the weights of copper to zinc in brass is 13:7.


∴ x = 245
∴ The weight of zinc in the brass utensil is 245 gm.

Case I:
If the value of x is 16, then the three consecutive whole numbers are
(16 – 1), 16,(16 + 1)i.e., 15, 16, 17
Case II:
If the value of x is 17, then the three consecutive whole numbers are (17 – 1), 17, (17 + 1) i.e., 16, 17, 18.
∴ The three consecutive whole numbers are 15, 16, 17 or 16, 17, 18.
Practice Set 12.2 8th Standard Question 5.
In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let the digit at unit’s place be x.
The digit at the ten’s place is twice the digit at unit’s place.
∴ The digit at ten’s place = 2x
Digit in units place | Digit in tens place | Number | |
Original Number | x | 2x | (2x × 10) + x = 20x + x = 21x |
New Number | 2x | x | (x × 10) + 2x = 10x + 2x = 12x |
Since, the sum of the original number and the new number is 66.
∴ 21x + 12x = 66
∴ 33x = 66
∴ x = 66/33
∴ x = 2
∴ Original number = 21x = 21 × 2 = 42
∴ the original number is 42.
Question 6.
Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let the number of tickets sold of Rs 100 be x.
The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100.
∴ Number of tickets sold of Rs 200 = (x + 20)
∴ Total amount received by the theatre through the sale of tickets = 100 × x + 200 × (x + 20)
= 100x + 200x + 4000
= 300x + 4000
Since, the total amount received by the theatre through the sale of tickets = Rs 37000
∴ 300x + 4000 = 37000
∴ 300x = 37000 – 4000
∴ 300x = 33000
∴ x = 33000/300
∴ x = 110
∴ 110 tickets of Rs 100 were sold.
Question 7.
Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let the three consecutive natural numbers be (x – 1), x and (x + 1).
Here, the smallest number is (x – 1) and the greatest number is (x + 1).
Since, five times the smallest number is 9 more than four times the greatest number.
∴ 5 × (x – 1) = [4 × (x + 1)] + 9
∴ 5x – 5 = 4x + 4 + 9
∴ 5x – 5 = 4x + 13
∴ 5x – 4x = 13 + 5
∴ x = 18 .
∴ the three numbers are (18 – 1), 18, (18 + 1)
i. e., 17, 18, 19
∴ The three consecutive natural numbers are 17,18 and 19.
Question 8.
Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let the cost price at which Raju purchased the bicycle be Rs x.
Since, Raju sold the bicycle at 8% profit to Amit.
∴ Selling price of bicycle for Raju = x + 8% of x
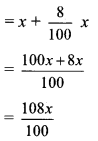
Since, Amit spent Rs 54 on repairing the bicycle and then sold it to Nikhil for Rs 1134, at no loss and no profit.
∴ Selling price of bicycle + repairing cost = Rs 1134
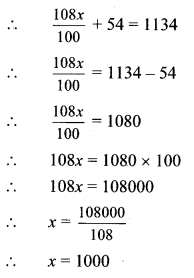
∴ The cost price of the bicycle at which Raju purchased it is Rs 1000.

Question 10.
Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let Viru’s present age be x years.
Sudhir’s present age is 5 more than three times the age of Viru.
∴ Sudhir’s present age = (3x + 5) years
Anil’s age is half the age of Sudhir.
![]()
Since, the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6.
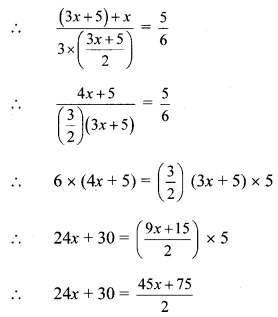
∴ 2 × (24x + 30) = 45x + 75
∴ 48x + 60 = 45x + 75
∴ 48x – 45x = 75 – 60
∴ 3x = 15
∴ x = 15/3
∴ x = 5
∴ Viru’s present age is 5 years.
Intext Questions and Activities
Question 1.
Write correct numbers in the boxes given. (Textbook pg. no. 78)
length is 3 times the breadth

Perimeter of the rectangle = 40
2(__x + __x) = 40
2 × __ x = 40
__ x = 40
x = __
∴ Breadth of rectangle = __ cm and Length of rectangle = __ cm
Solution:
length is 3 times the breadth

Perimeter of the rectangle = 40
∴ 2(3x + 1x) = 40
∴ 2 × 4x = 40
∴ 8x = 40
∴ x = 5
∴ Breadth of rectangle = 5 cm and Length of rectangle = 15 cm