Chapter 13 Pythagoras Theorem Set 13.1
Question 1.
In the figures below, find the value of ‘x’.

Solution:
i. In ∆LMN, ∠M = 90°.
Hence, side LN is the hypotenuse.
According to Pythagoras’ theorem,
l(LN)² = l(LM)² + l(MN)²
∴ x² = 72 + 24²
∴ x² = 49 + 576
∴ x² = 625
∴ x² = 25²
∴ x = 25 units
ii. In ∆PQR, ∠Q = 90°.
Hence, side PR is the hypotenuse.
According to Pythagoras’ theorem,
l(PR)² = l(PQ)² + l(QR)²
∴ 412 = 92 + x²
∴ 1681 = 81 + x²
∴ 1681 – 81 = x²
∴ 1600 = x²
∴ x² = 1600
∴ x² = 40²
∴ x = 40 units
iii. In AEDF, ∠D = 90°.
Hence, side EF is the hypotenuse.
According to Pythagoras’ theorem,
l(EF)² = l(ED)² + l(DF)²
∴ 17² = x² + 8²
∴ 289 = x² + 64
∴ 289 – 64 = x²
∴ 225 = x²
∴ x² = 225
∴ x² = 15²
∴ x = 15 units
Question 2.
In the right-angled ∆PQR, ∠P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
Solution:
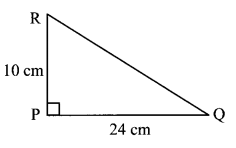
In ∆PQR, ∠P = 90°.
Hence, side QR is the hypotenuse.
According to Pythagoras’ theorem,
l(QR)² = l(PR)² + l(PQ)²
∴ l(QR)² = 10² + 24²
∴ l(QR)² = 100 + 576
∴ l(QR)² =676
∴ l(QR)² = 26²
∴ l(QR) = 26 cm
∴ The length of seg QR is 26 cm.
Question 3.
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
Solution:
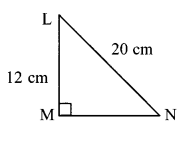
In ∆LMN, ∠M = 90°.
Hence, side LN is the hypotenuse.
According to Pythagoras’ theorem,
l(LN)² = l(LM)² + l(MN)²
∴ 20² = 12² + l(MN)²
∴ l(MN)² = 20² – 12²
∴ l(MN)² = 400 – 144
∴ l(MN)² = 256
∴ l(MN)² = 16²
∴ l(MN)= 16 cm
∴ The length of seg MN is 16 cm.
Question 4.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
Solution:
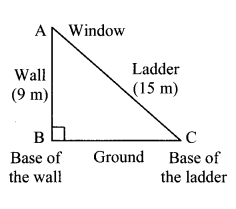
The wall and the ground are perpendicular to each other. Hence, the ladder leaning against the wall forms a right-angled triangle.
In ∆ABC, ∠B = 90°
According to Pythagoras’ theorem,
l(AC)² = l(AB)² + l(BC)²
∴ 15² = l(BC)² + 9²
∴ 225 = l(BC)² + 81
∴ 225 – 81 = l(BC)²
∴ 144 = l(BC)²
∴ 12² = l(BC)²
∴ l(BC) = 12
∴ The distance between the base of the wall and that of the ladder is 12 m.
Intext Questions and Activities
Question 1.
Write the name of the hypotenuse of each of the rightangled triangles shown below.
i.
The hypotenuse of ∆ABC is__
ii.

The hypotenuse of ∆LMN is__
iii.
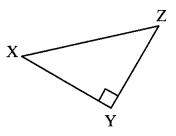
The hypotenuse of ∆XYZ is__
Solution:
i. AC
ii. MN
iii. XZ
Question 2.
Draw right-angled triangles with the lengths of hypotenuse and one side as shown in the rough figures below. Measure the third side. Verify the Pythagoras’ theorem. (Textbook pg. no. 87)
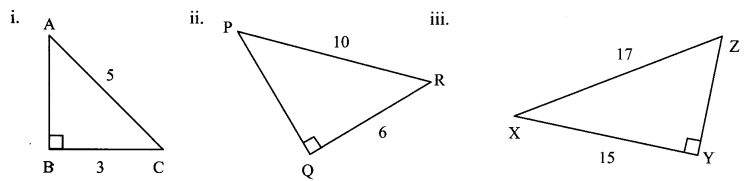
Solution:
i. From the figure, by measurement,
l(AB) = 4 cm
Now, in right-angled triangle ABC,
l(AB)² + l(BC)² = (4)² + (3)²
= 16 + 9
∴ l(AB)² + l(BC)² = 25 …. (i)
l(AC)² = (5)² = 25 ….(ii)
∴ From (i) and (ii),
l(AC)² = l(AB)² + l(BC)²
∴ Pythagoras’ theorem is verified.
(Students should draw the triangles PQR and XYZ and verify the Pythagoras ’ theorem)
Question 3.
Without using a protractor, can you verify that every angle of the vacant quadrilateral in the adjacent figure is a right angle? (Textbook pg. no. 89)
Solution:
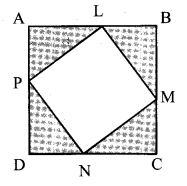
In the square ABCD the shaded triangles are right-angled and are the same.
In ∆LBM,
m∠BLM + m∠BML + m∠LBM = 180° …. (Sum of the measures of the angles of a triangles is 180° )
∴ m∠BLM + m∠BML + 90° = 180°
∴ m∠BLM + m∠BML = 90° …. (i)
Now, ∆LBM and ∆LAP are same.
∴ m∠BML = m∠ALP …. (ii)
∴ m∠BLM + m∠ALP = 90° …. IFrom (i) and (ii)l
Now, m∠ALP + m∠PLM + m∠BLM = 180° …. (The measure of a straight angle is 180°)
∴ m∠ALP + m∠BLM + m∠PLM = 180°
∴ 90° + m∠PLM = 180°
∴ m∠PLM = 180°- 90° = 90°
∴ m∠PLM is a right angle.
Similarly, we can prove that the other angles of the vacant quadrilateral are right angles.
Question 4.
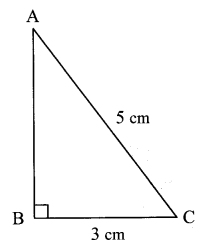
On a sheet of card paper, draw a right-angled triangle of sides 3 cm, 4 cm and 5 cm. Construct a square on each of the sides. Find the area of each of the squares and verify Pythagoras’ theorem. (Textbook pg. no. 89)
Solution:
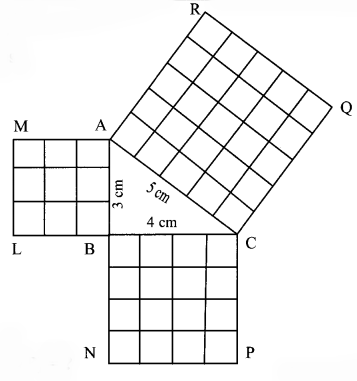
Area of square ABLM = l(AB)² = 32 = 9 sq.cm
Area of square BCPN = l(BC)²= 42 = 16 sq.cm
Area of square ACQR = l(AC)² = 52 = 25 sq.cm
Now, 25 = 16 + 9
i.e. 5² = 4² + 3²
∴ l(AC)² = l(BC)² + l(AB)²
∴ (hypotenuse)² = (base)² + (height)²