Blog

Chapter 15 Structure of Atoms and Nuclei

Chapter 15 Structure of Atoms and Nuclei

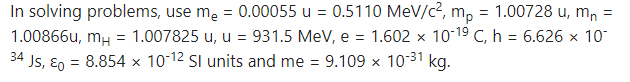
1. Choose the correct option.

i) In which of the following systems will the radius of the first orbit of the electron be the smallest?
(A) hydrogen
(B) singly ionized helium
(C) deuteron
(D) tritium
Answer:
(D) tritium

ii) The radius of the 4th orbit of the electron will be smaller than its 8th orbit by a factor of
(A) 2
(B) 4
(C) 8
(D) 16
Answer:
(B) 4

iii) In the spectrum of hydrogen atom which transition will yield longest wavelength?
(A) n = 2 to n = 1
(B) n = 5 to n = 4
(C) n = 7 to n = 6
(D) n = 8 to n = 7
Answer:
(D) n = 8 to n = 7

iv) Which of the following properties of a nucleus does not depend on its mass number?
(A) radius
(B) mass
(C) volume
(D) density
Answer:
(D) density

v) If the number of nuclei in a radioactive sample at a given time is N, what will be the number at the end of two half-lives?

2. Answer in brief.

i) State the postulates of Bohr’s atomic model.
Answer:
The postulates of Bohr’s atomic model (for the hydrogen atom) :

1. The electron revolves with a constant speed in acircular orbit around the nucleus. The necessary centripetal force is the Coulomb force of attraction of the positive nuclear charge on the negatively charged electron.
2. The electron can revolve without radiating energy only in certain orbits, called allowed or stable orbits, in which the angular momentum of the electron is equal to an integral multiple of h/2π, where h is Planck’s constant.
3. Energy is radiated by the electron only when it jumps from one of its orbits to another orbit having lower energy. The energy of the quantum of elec-tromagnetic radiation, i.e., the photon, emitted is equal to the energy difference of the two states.

ii) State the difficulties faced by Rutherford’s atomic model.
Answer:
(1) According to Rutherford, the electrons revolve in circular orbits around the atomic nucleus. The circular motion is an accelerated motion. According to the classical electromagnetic theory, an accelerated charge continuously radiates energy. Therefore, an electron during its orbital motion, should go on radiating energy. Due to the loss of energy, the radius of its orbit should go on decreasing. Therefore, the electron should move along a spiral path and finally fall into the nucleus in a very short time, of the order of 10^-16 s in the case of a hydrogen atom. Thus, the atom should be unstable. We exist because atoms are stable.

(2) If the electron moves along such a spiral path, the radius of its orbit would continuously decrease. As a result, the speed and frequency of revolution of the electron would go on increasing. The electron, therefore, would emit radiation of continuously changing frequency, and hence give rise to a con-tinuous spectrum. However, atomic spectrum is a line spectrum.

where v_e is the neutrino emitted to conserve the momentum, energy and spin.
Q = [m_P – m_Si – m_e]c²
[Note : The term fi particle refers to the electron (or positron) emitted by a nucleus.]

A given nucleus does not emit α and β-particles simultaneously. However, on emission of α or β-particles, most nuclei are left in an excited state. A nucleus in an excited state emits a γ-ray photon in a transition to the lower energy state. Hence, α and β-particle emissions are often accompanied by γ-rays.

iv) Define excitation energy, binding energy and ionization energy of an electron in an atom.
Answer:
(1) Excitation energy of an electron in an atom : The energy required to transfer an electron from the ground state to an excited state (a state of higher energy) is called the excitation energy of the electron in that state.

(2) Binding energy of an electron in an atom is defined as the minimum energy that should be provided to an orbital electron to remove it from the atom such that its total energy is zero.

(3) Ionization energy of an electron in an atom is defined as the minimum energy required to remove the least strongly bound electron from a neutral atom such that its total energy is zero.

v) Show that the frequency of the first line in Lyman series is equal to the difference between the limiting frequencies of Lyman and Balmer series.
Answer:


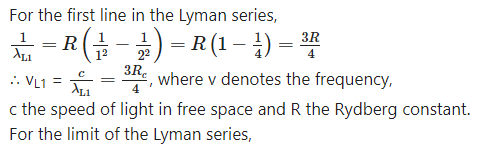
Hence, the result.

Question 3.
State the postulates of Bohr’s atomic model and derive the expression for the energy of an electron in the atom.
Answer:
The postulates of Bohr’s atomic model (for the hydrogen atom) :
(1) The electron revolves with a constant speed in acircular orbit around the nucleus. The necessary centripetal force is the Coulomb force of attraction of the positive nuclear charge on the negatively charged electron.
(2) The electron can revolve without radiating energy only in certain orbits, called allowed or stable orbits, in which the angular momentum of the electron is equal to an integral multiple of h/2π, where h is Planck’s constant.
(3) Energy is radiated by the electron only when it jumps from one of its orbits to another orbit having lower energy. The energy of the quantum of elec-tromagnetic radiation, i.e., the photon, emitted is equal to the energy difference of the two states.

Consider the electron revolving in the nth orbit around the nucleus of an atom with the atomic number Z. Let m and e be the mass and the charge of the electron, r the radius of the orbit and v the linear speed of the electron.

This shows that the total energy of the electron in the nth orbit of the atom is inversely proportional to the radius of the orbit as Z, ε₀ and e are constants. The radius of the nth orbit of the electron is

Question 4.
Starting from the formula for energy of an electron in the n^th orbit of hydrogen atom, derive the formula for the wavelengths of Lyman and Balmer series spectral lines and determine the shortest wavelengths of lines in both these series.
Answer:
According to Bohr’s third postulate for the model of the hydrogen atom, an atom radiates energy only when an electron jumps from a higher energy state to a lower energy state and the energy of the
quantum of electromagnetic radiation emitted in this process is equal to the energy difference between the two states of the electron. This emission of radiation gives rise to a spectral line.

This energy is emitted in the form of a quantum of radiation (photon) with energy hv, where V is the frequency of the radiation.

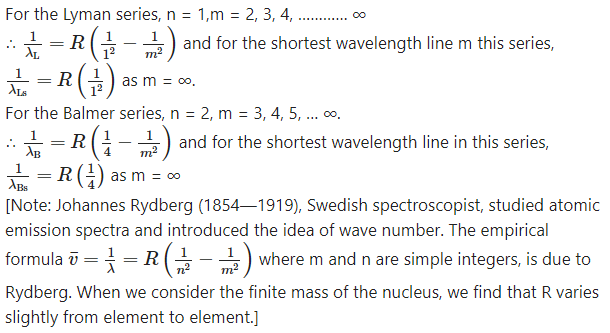
Question 5.
Determine the maximum angular speed of an electron moving in a stable orbit around the nucleus of hydrogen atom.
Answer:

Obtain the formula for ω and continue as follows :

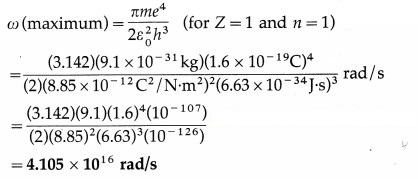
This is required quantity.

Question 6.
Determine the series limit of Balmer, Paschen and Bracket series, given the limit for Lyman series is 912 Å.
Answer:
Data : λ_L∞ = 912 Å

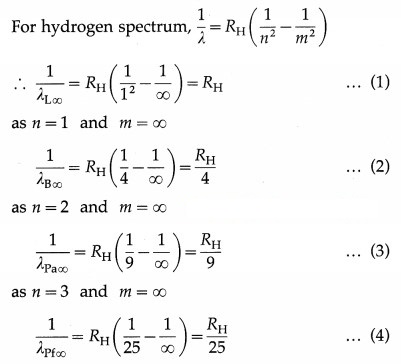
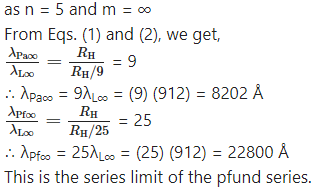
Question 7.
Describe alpha, beta and gamma decays and write down the formulae for the energies generated in each of these decays.
Answer:

A given nucleus does not emit α and β-particles simultaneously. However, on emission of α or β-particles, most nuclei are left in an excited state. A nucleus in an excited state emits a γ-ray photon in a transition to the lower energy state. Hence, α and β-particle emissions are often accompanied by γ-rays.

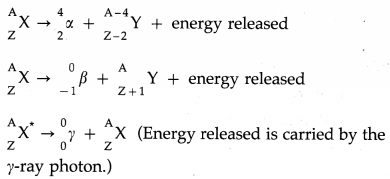
Question 8.
Explain what are nuclear fission and fusion giving an example of each. Write down the formulae for energy generated in each of these processes.
Answer:
Nuclear fission is a nuclear reaction in which a heavy nucleus of an atom, such as that of uranium, splits into two or more fragments of comparable size, either spontaneously or as a result of bombardment of a neutron on the nucleus (induced fission). It is followed by emission of two or three neutrons.
The mass of the original nucleus is more than the sum of the masses of the fragments. This mass difference is released as energy, which can be enormous as in the fission of ²³⁵U.
Nuclear fission was discovered by Lise Meitner, Otto Frisch, Otto Hahn and Fritz Strassmann in 1938.

The products of the fission of ²³⁵U by thermal neutrons are not unique. A variety of fission fragments are produced with mass number A ranging from about 72 to about 138, subject to the conservation of mass-energy, momentum, number of protons (Z) and number of neutrons (N). A few typical fission equations are

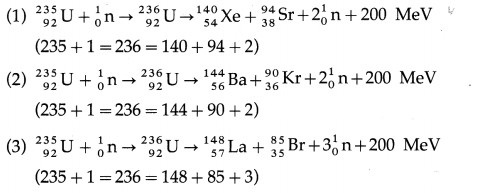
A type of nuclear reaction in which lighter atomic nuclei (of low atomic number) fuse to form a heavier nucleus (of higher atomic number) with the’ release of enormous amount of energy is called nuclear fusion.

Very high temperatures, of about 107 K to 108 K, are required to carry out nuclear fusion. Hence, such a reaction is also called a thermonuclear reaction.

Example : The D-T reaction, being used in experimental fusion reactors, fuses a deuteron and a triton nuclei at temperatures of about 10⁸ K.

(2) The value of the energy released in the fusion of two deuteron nuclei and the temperature at which the reaction occurs mentioned in the textbook are probably misprints.]

Question 9.
Describe the principles of a nuclear reactor. What is the difference between a nuclear reactor and a nuclear bomb?

In a nuclear reactor, a nuclear fission chain reaction is used in a controlled manner, while in a nuclear bomb, the nuclear fission chain reaction is not controlled, releasing tremendous energy in a very short time interval.
[Note : The first nuclear bomb (atomic bomb) was dropped on Hiroshima in Japan on 06 August 1945. The second bomb was dropped on Nagasaki in Japan on 9 August 1945.]

Question 10.
Calculate the binding energy of an alpha particle given its mass to be 4.00151 u.
Answer:
Data : M = 4.00151 u, = 1.00728 u,
m_n = 1.00866 u, 1 u = 931.5 MeV/c²
The binding energy of an alpha particle
(Zm_p + N_n -M)c²
=(2m_p + 2m_n -M)c²
= [(2)(1.00728u) + 2(1.00866 u) – 4.00151 u]c²
= (2.01456 + 2.01732 – 4.00151)(931.5) MeV
= 28.289655 MeV
= 28.289655 × 10⁶ eV × 1.602 × 10^-19 J
= 4.532002731 × 10^-12 J

Question 11.
An electron in hydrogen atom stays in its second orbit for 10^-8 s. How many revolutions will it make around the nucleus in that time?
Answer:
Data : z = 1, m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C, ε₀ = 8.85 × 10^-12 C² / N.m², h = 6.63 × 10 ^-34 J.s, n = 2, t = 10^-8 s
The periodic time of the electron in a hydrogen atom,

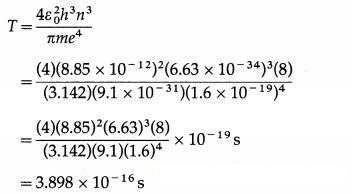
Answer:
Data : Z = 95, N = 244  – 95 = 149,
m_p = 1.00728 u, m_n = 1.00866 u,
M = 244.06428 u, 1 u = 931.5 MeV/c²
The binding energy per nucleon,

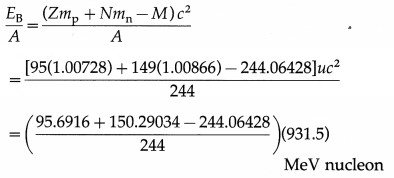
= 7.3209 MeV/nucleon

Question 14.
Complete the following equations describing nuclear decays.

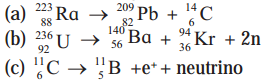
Answer:

Question 16.
Sample of carbon obtained from any living organism has a decay rate of 15.3 decays per gram per minute. A sample of carbon obtained from very old charcoal shows a disintegration rate of 12.3 disintegrations per gram per minute. Determine the age of the old sample given the decay constant of carbon to be 3.839 × 10^-12 per second.
Answer:
Data: 15.3 decays per gram per minute (living organism), 12.3 disintegrations per gram per minute (very old charcoal). Hence, we have,

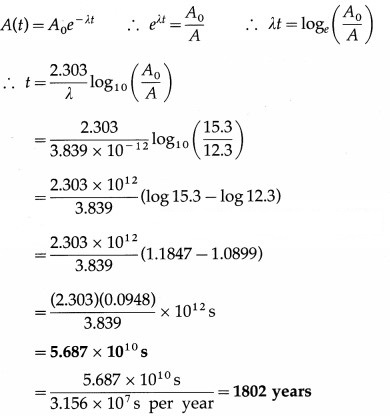
Question 18.

Answer:

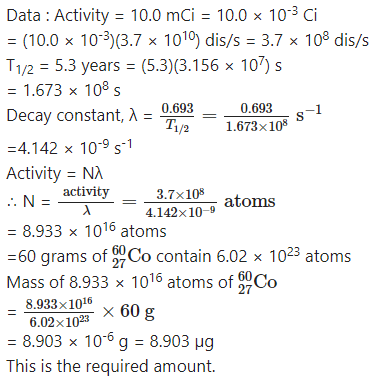
Question 19.
Disintegration rate of a sample is 10¹⁰ per hour at 20 hrs from the start. It reduces to 6.3 × 10⁹ per hour after 30 hours. Calculate its half life and the initial number of radioactive atoms in the sample.
Answer:
Data : A (t₁) = 10¹⁰ per hour, where t₁ = 20 h,
A (t₂) = 6.3 × 10⁹ per hour, where t₂ = 30 h
A(t) = A₀e^-λt ∴ A(t₁) = A₀e^-λt₁ and A(t₂) = A_oe^-λt₂

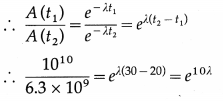
Question 20.
The isotope ⁵⁷Co decays by electron capture to ⁵⁷Fe with a half-life of 272 d. The ⁵⁷Fe nucleus is produced in an excited state, and it almost instantaneously emits gamma rays.
(a) Find the mean lifetime and decay constant for ⁵⁷Co.
(b) If the activity of a radiation source ⁵⁷Co is 2.0 µCi now, how many ⁵⁷Co nuclei does the source contain?
(c) What will be the activity after one year?
Answer:

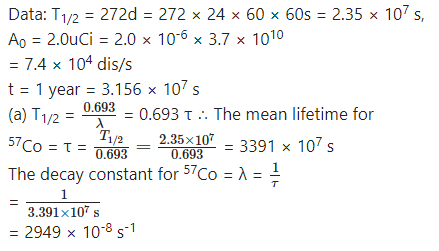
Question 21.

Answer:

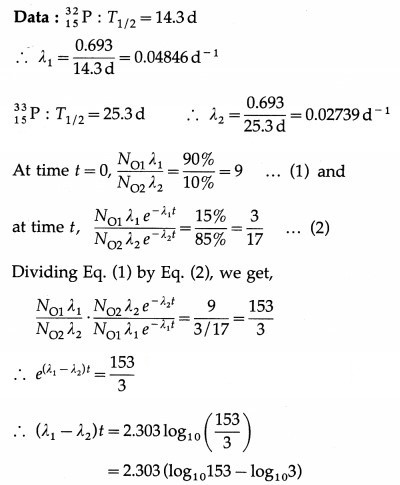
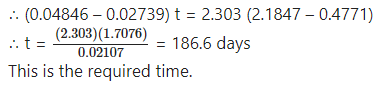
Question 22.
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of ¹⁴C averaged about 0.255 Bq per gram of carbon. (a) What fraction of carbon atoms were ¹⁴C? (b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? Half-life of 14C is 5730 years?
Answer:

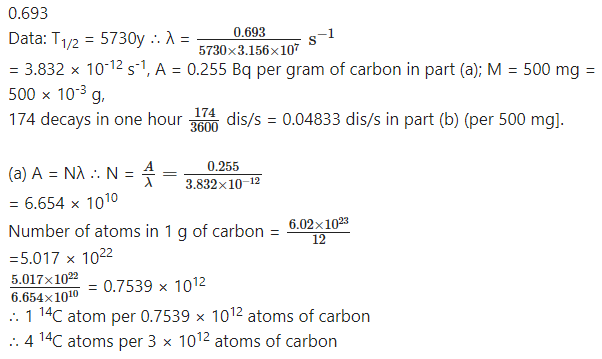
(b) Present activity per gram = 
= 0.09666 dis/s per gram
A₀ = 0.255 dis/s per gram
Now, A(t) = A₀e^-λt

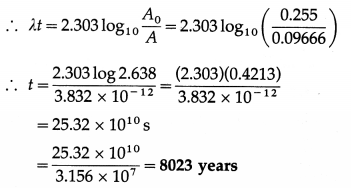
This is the required quantity.

Question 23.
How much mass of ²³⁵U is required to undergo fission each day to provide 3000 MW of thermal power? Average energy per fission is 202.79 MeV
Answer:

Question 24.

[Answer: 9.3% and 11.7%]
Answer:
Data : Average atomic mass of magnesium =

Questions and Answers

Use your brain power (Textbook Page No. 336)

Question 1.
Why don’t heavy nuclei decay by emitting a single proton or a single neutron?
Answer:
According to quantum mechanics, the probability for these emissions is extremely low.