Blog

Chapter 15 Triangles and their Properties

Question 1.
Observe the figures below and write the type of the triangle based on its angles:

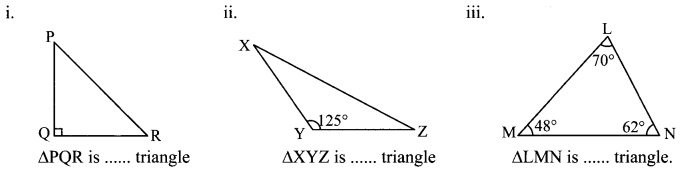
Solution:
i. right angled
ii. Obtuse angled
iii. acute angled

Question 2.
Observe the figures below and write the type of the triangle based on its sides:

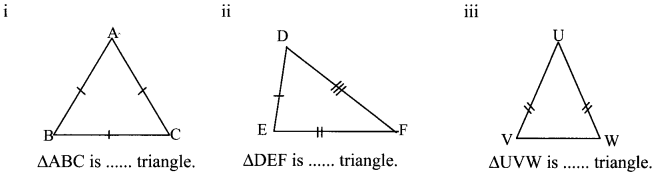
Solution:
i. equilateral
ii. scalene
iii. isosceles

Question 3.
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.

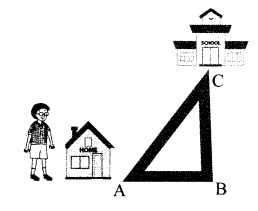
Solution:
The two roads which Avinash can choose to go to school are

1. Road AB + Road BC
2. Road AC

The three roads together form ∆ABC.
Road AC is shorter because the sum of the lengths of any two sides (side AB + side BC) of a triangle is always greater than the third side (side AC).

Question 4.
The lengths of the sides of some triangles are given. Say what types of triangles they are.

1. 3 cm, 4 cm, 5 cm
2. 3.4 cm, 3.4 cm, 5 cm
3. 4.3 cm, 4.3 cm, 4.3 cm
4. 3.7 cm, 3.4 cm, 4 cm

Solution:

1. Since, no two sides have equal lengths, the given triangle is a scalene triangle.
2. Since, two sides have equal length, the given triangle is an isosceles triangle.
3. Since, all the three sides have equal lengths, the given triangle is an equilateral triangle.
4. Since, no two sides have equal lengths, the given triangle is a scalene triangle.

Question 5.
The lengths of the three segments are given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
i. 17 cm, 7 cm, 8 cm
ii. 7 cm, 24 cm, 25 cm
iii. 9 cm, 6 cm, 16 cm
iv. 8.4 cm, 16.4 cm, 4.9 cm
v. 15 cm, 20 cm, 25 cm
vi. 12 cm, 12 cm, 16 cm
Solution:
i. The lengths of the three sides are 17 cm, 7 cm, 8 cm.
a. 7 cm + 17 cm = 24 cm, greater than 8 cm
b. 8 cm +17 cm = 25 cm, greater than 7 cm
c. 7 cm + 8 cm =15 cm, not greater than 17 cm
The sum of lengths of two sides in (c) is not greater than the length of the third side.
∴ Triangle cannot be drawn with sides 17 cm, 7 cm, 8 cm.

ii. The lengths of the three sides are 7 cm, 24 cm, 25 cm.
a. 7 cm + 24 cm = 31 cm, greater than 25 cm
b. 25 cm + 7 cm = 32 cm, greater than 24 cm
c. 24 cm + 25 cm = 49 cm, greater than 7 cm
The sum of lengths of two sides is greater than the length of the third side.
∴ Triangle can be drawn with sides 7 cm, 24 cm, 25 cm.

iii. The lengths of the three sides are 9 cm, 6 cm, 16 cm.
a. 9 cm + 16 cm = 25 cm, greater than 6 cm
b. 6 cm + 16 cm = 22 cm, greater than 9 cm
c. 9 cm+ 6 cm =15 cm, not greater than 16 cm
The sum of lengths of two sides in (c) is not greater than the length of the third side.
∴ Triangle cannot be drawn with sides 9 cm, 6 cm, 16 cm.

iv. The lengths of the three sides are 8.4 cm, 16.4 cm, 4.9 cm.
a. 8.4 cm + 16.4 cm = 24.8 cm, greater than 4.9 cm
b. 4.9 cm + 16.4 cm = 21.3 cm, greater than 8.4 cm
c. 8.4 cm + 4.9 cm = 13.3 cm, not greater than 16.4 cm
The sum of lengths of two sides in (c) is not greater than the length of the third side.
∴ Triangle cannot be drawn with sides 8.4 cm, 16.4 cm, 4.9 cm.

v. The lengths of the three sides are 15 cm, 20 cm, 25 cm.
a. 15 cm + 20 cm = 35 cm, greater than 25 cm
b. 25 cm + 20 cm = 45 cm, greater than 15 cm
c. 15 cm + 25 cm = 40 cm, greater than 20 cm
The sum of lengths of two sides is greater than the length of the third side.
∴ Triangle can be drawn with sides 15 cm, 20 cm, 25 cm.

vi. The lengths of the three sides are 12 cm, 12 cm, 16 cm.
a. 12 cm + 12 cm = 24 cm, greater than 16 cm
b. 12 cm + 16 cm = 28 cm, greater than 12 cm
c. 12 cm + 16 cm = 28 cm, greater than 12 cm
The sum of lengths of two sides is greater than the length of the third side.
∴ Triangle can be drawn with sides 12 cm, 12 cm, 16 cm.

Intext Questions and Activities

Question 1.
In the given figure, some points and some line segments joining them have been drawn. Which of these figures is a triangle? Which figure is not a triangle? Why not? (Textbook pg. no. 77)

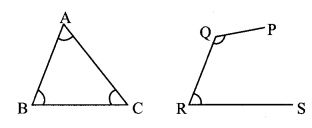
Solution:
ABC it is a closed figure with three sides. Hence, ABC is a triangle.
PQRS has three sides but it is not a closed figure. Hence, PQRS is not a triangle.

Question 2.
As seen above, ∆ABC has three sides. Line segment AB is one side. Write the names of the other two sides. ∆ABC has three angles. ∠ABC is one among them. Write the names of the other angles. (Textbook pg. no. 77)
Solution:
The names of other two sides are: seg BC and seg AC
The names of other angles are: ∠BCA and ∠CAB

Question 3.
Measure the sides of the following triangles in centimeters, using a divider and ruler. Enter the lengths in the table below. What do you observe? (Textbook pg. no. 77)

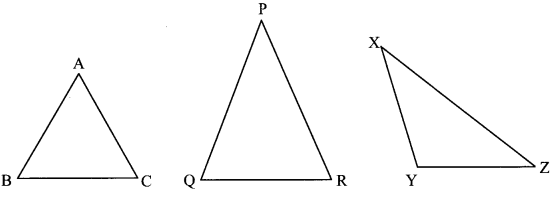
In ∆ABC	In ∆PQR	In ∆XYZ
l (AB) =       cm	l (QR) =       cm	l (XY) =       cm
l (BC) =       cm	l (PQ) =       cm	l (YZ) =       cm
l (AC) =       cm	l (PR) =        cm	l (XZ) =       cm

Solution:

In ∆ABC	In ∆PQR	In ∆XYZ
l (AB) = 2.6 cm	l (QR) = 2.8 cm	l (XY) = 2.8 cm
l (BC) = 2.6 cm	l (PQ) = 3.8 cm	l (YZ) = 2.6 cm
l (AC) = 2.6 cm	l (PR) = 3.8 cm	l (XZ) = 4.3 cm

We observe that,

1. ∆ABC is an equilateral triangle,
2. ∆PQR is an isosceles triangle, and
3. ∆XYZ is a scalene triangle.

Question 4.
Measure all the angles of the triangles given below. Enter them in the following table. (Textbook pg. no. 78)

In ∆DEF	In ∆PQR	In ∆LMN
Measure of ∠D = m ∠D =___	Measure of ∠P = m ∠P =___	Measure of ∠L =__
Measure of ∠E = m ∠E =___	Measure of ∠Q =___=___	Measure of ∠M =___
Measure of ∠F = ___=___	Measure of ∠R =___=___	Measure of ∠N =___
Observation: All three angles are acute angles.	Observation: One angle is right angle and two are acute angles.	Observation: One angle is an obtuse angle and two are acute.

Solution:

In ∆DEF	In ∆PQR	In ∆LMN
Measure of ∠D = m ∠D = 60º	Measure of ∠P = m ∠P = 45º	Measure of ∠L = 30º
Measure of ∠E = m ∠E = 68º	Measure of ∠Q = m = 90º	Measure of ∠M = 116º
Measure of ∠F = m = 52º	Measure of ∠R = m ∠R = 45º	Measure of ∠N = 34º

1. ADEF is an acute angled triangle,
2. APQR is a right angled triangle,
3. ALMN is an obtuse angled triangle.

Question 5.
Observe the set squares in your compass box. What kind of triangles are they? (Textbook pg. no. 78)

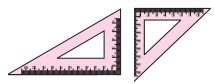
Solution:
The first set square is a scalene triangle and also a right angled triangle.
The second set square is an isosceles triangle and also a right angled triangle.

Question 6.
Properties of a triangle. (Textbook pg. no. 79)
Take a triangular piece of paper. Choose three different colors or signs to mark the three comers of the triangle on both sides of the paper. Fold the paper at the midpoints of two sides as observe?

Solution:
The three angles of the triangle form a straight angle.
∴ m∠A + m∠B + m∠C = 180°
Hence, the sum of the measures of the angles of a triangle is 180°.

Question 7.
Properties of a triangle (Textbook pg. no. 79)
Take a triangular piece of paper and make three different types of marks near the three angles. Take a point approximately at the center of the triangle. From this point, draw three lines that meet the three sides. Cut the paper along those lines. Place the three angles side by side as shown. See how the three angles of a triangle together form a straight angle, or, an angle that measures 180°.

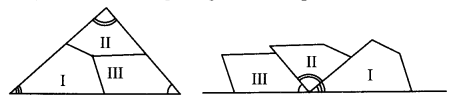
Solution:
The three angles of the triangle form a straight angle.
Hence, the sum of the measures of the angles of a triangle is 180°.

Question 8.
Draw any triangle on a paper. Name its vertices A, B, C. Measure the lengths of its three sides using a divider and scale and enter them in the table. (Textbook pg. no. 79)

Length of side	Sum of the lengths of two sides	Length of the third side
l (AB) =         cm	l (AB) + l (BC) =         cm	l (AC) =         cm
l (BC) =         cm	l (BC) + l (AC) =         cm	l (AB) =         cm
l (AC) =         cm	l (AC) + l (AB) =        cm	l (BC) =         cm

Solution:

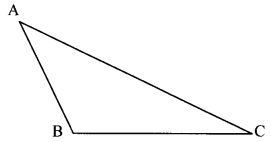
Length of side	Sum of the lengths of two sides	Length of the third side
l (AB) = 2.7 cm	l (AB) + l (BC) = 6.6 cm	l (AC) = 5.6 cm
l (BC) = 2.9 cm	l (BC) + l (AC) = 9.5 cm	l (AB) = 2.7 cm
l (AC) = 5.6 cm	l (AC) + l (AB) = 8.3 cm	l (BC) = 3.9 cm