Blog

Chapter 16 Quadrilaterals Set 16.1

Question 1.
Observe the figures below and find out their names:

Solution:
i. Pentagon (5 sides)
ii. Hexagon (6 sides)
iii. Heptagon (7 sides)
iv. Octagon (8 sides)

Intext Questions and Activities

Question 1.
Observe the figures given below and say which of them are quadrilaterals. (Textbook pg. no. 81)

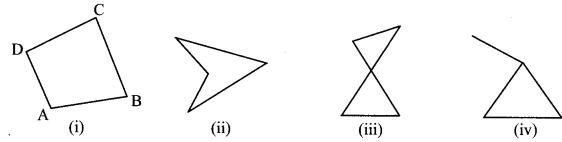
Solution:
Is a quadrilateral: (i)

Question 2.
Draw a quadrilateral. Draw one diagonal of this quadrilateral and divided it into two triangles. Measures all the angles in the figure. Is the sum of the measures of the four angles of the quadrilateral equal to the sum of the measures of the six angles of the two triangles? Verity that this is so with other quadrilaterals. (Textbook pg. no. 84)
Solution:

m∠PQR = 104°
m∠QRP = 26°
m∠RPQ = 50°
m∠PRS = 34°
m∠RSP = 106°
m∠SPR = 40°
∴ Sum of the measures of the angles of quadrilateral = m∠PQR + m∠QRP + m∠RPQ + m∠PRS + m∠RSP + m∠SPR
= 104° + 26° + 50° + 34° + 106° + 40°
= 360°
Also, we observe that
Sum of the measures of the angles of quadrilateral = Sum of the measures of angles of the two triangles (PQR and PRS)
= (104°+ 26°+ 50°)+ (34° + 106° + 40°)
= 180° + 180°
= 360°
[Note: Students should drew different quadrilaterals and verify the property.]

Question 3.
For the pentagon shown in the figure below, answer the following: (Textbook pg. no. 84)

1. Write the names of the five vertices of the pentagon.
2. Name the sides of the pentagon.
3. Name the angles of the pentagon.
4. See if you can sometimes find players on a field forming a pentagon.

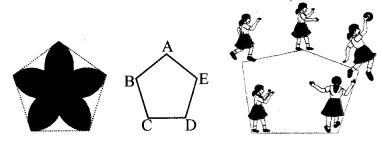
Solution:

1. The vertices of the pentagon are points A, B, C, D and E.
2. The sides of the pentagon are segments AB, BC, CD, DE and EA.
3. The angles of the pentagon are ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB.
4. The players shown in the above figure form a pentagon. The players are standing on the vertices of

Question 4.
Cut out a paper in the shape of a quadrilateral. Make folds in it that join the vertices of opposite angles. What can these folds be called? (Textbook pg. no. 83)

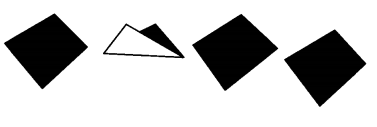
Solution:
The folds are called diagonals of the quadrilateral.

Question 5.
Take two triangular pieces of paper such that . one side of one triangle is equal to one side of the other. Let us suppose that in ∆ABC and ∆PQR, sides AC and PQ are the equal sides. Join the triangles so that their equal sides lie B side by side. What figure do we get? (Textbook pg. no. 83)

Solution:
If we place the triangles together such that the equal sides overlap, the two triangles form a quadrilateral.