Blog

Chapter 16 Quadrilaterals Set 16.2

Question 1.
Draw ₹XYZW and answer the following:
i. The pairs of opposite angles.
ii. The pairs of opposite sides.
iii. The pairs of adjacent sides.
iv. The pairs of adjacent angles.
v. The diagonals of the quadrilateral.
vi. The name of the quadrilateral in different ways.
Solution:

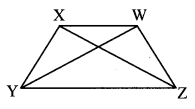
i. a. ∠XYZ and ∠XWZ
b. ∠YXW and ∠YZW

ii. a. side XY and side WZ
b. side XW and side YZ

iii. a. side XY and side XW
b. side WX and side WZ
c. side ZW and side ZY
d. side YZ and side YX

iv. a. ∠XYZ and ∠YZW
b. ∠YZW and ∠ZWX
c. ∠ZWX and ∠WXY
d. ∠WXY and ∠XYZ

v. Seg XZ and seg YW

vi. ₹XYZW
₹YZWX
₹ZWXY
₹WXYZ
₹XWZY
₹WZYX
₹ZYXW
₹YXWZ

Question 2.
In the table below, write the number of sides the polygon has.

Names	Quadrilateral	Octagon	Pentagon	Heptagon	Hexagon
Number of sides

Solution:

Names	Quadrilateral	Octagon	Pentagon	Heptagon	Hexagon
Number of sides	4	8	5	7	6

Question 3.
Look for examples of polygons in your surroundings. Draw them.
Solution:

Question 4.
We see polygons when we join the tips of the petals of various flowers. Draw these polygons and write down the number of sides of each polygon.
Solution:

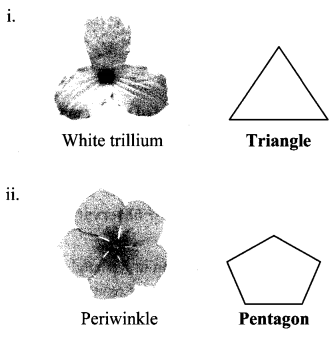
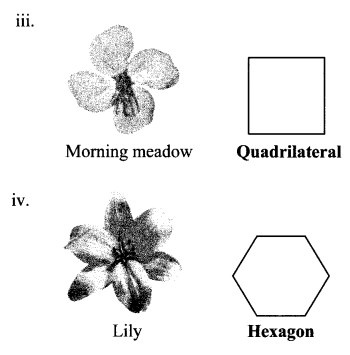
Question 5.
Draw any polygon and divide it into triangular parts as shown here. Thus work out the sum of the measures of the angles of the polygon.

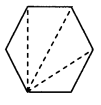
Solution:

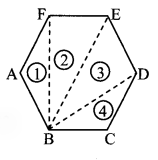
Hexagon ABCDEF can be divided in 4 triangles namely ∆BAF, ∆BFE, ∆BED and ∆BCD
Sum of the measures of the angles of a triangle = 180°
∴ Sum of measures of the angles of the polygon ABCDEF = Sum of the measures of all the four triangles
= 180° + 180° + 180°+ 180°
= 720°
∴ The sum of the measures of the angles of the given polygon (hexagon) is 720°.

Intext Questions and Activities

Question 1.
From your compass boxes, collect set squares of the same shapes and place them side by side in all possible different ways. What figures do you get? Write their names. (Textbook pg. no. 85)
a. Two set squares
b. Three set squares
c. four set squares
Solution:
a. Two set squares

b. Three set squares

c. four set squares

Question 2.
Kaprekar Number. (Textbook pg. no. 86)
i. Take any 4-digit number in which all the digits are not the same.
ii. Obtain a new 4-digit number by arranging the digits in descending order.
iii. Obtain another 4-digit number by arranging the digits of the new number in ascending order.
iv. Subtract the smaller of these two new numbers from the bigger number. The difference obtained will be a 4-digit number. If it is a 3-digit number, put a 0 in the thousands place. Repeat the above steps with the difference obtained as a result of the subtraction.
v. After some repetitions, you will get the number 6174. If you continue to repeat the same steps you will get the number 6174 every time. Let us begin with the number 8531.
8531 → 7173 → 6354 → 3087 → 8352 → 6174 → 6174
This discovery was made by the mathematician, Dattatreya Ramchandra Kaprekar. That is why the number 6174 was named the Kaprekar number.
Solution: