Chapter 16 Surface Area and Volume Set 16.1
Question 1.
Find the volume of a box if its length, breadth and height are 20 cm, 10.5 cm and 8 cm respectively.
Given: For cuboid shaped box,
length (l) = 20 cm, breadth (b) = 10.5 cm and height (h) = 8cm
To find: Volume of a box
Solution:
Volume of a box = l x b x h
= 20 x 10.5 x 8
= 1680 cc
∴ The volume of the box is 1680 cc.
Question 2.
A cuboid shaped soap bar has volume 150 cc. Find its thickness if its length is 10 cm and breadth is 5 cm.
Given: For cuboid shaped soap bar,
length (l) = 10 cm, breadth (b) = 5 cm and volume = 150 cc
To find: Thickness of the soap bar (h)
Solution:
Volume of soap bar = l x b x h
∴ 150 = 10 x 5 x h
∴ 150 = 50h
∴ 150/50=h
∴ 3 = h
i.e., h = 3 cm
∴ The thickness of the soap bar is 3 cm.
Question 3.
How many bricks of length 25 cm, breadth 15 cm and height 10 cm are required to build a wall of length 6 m, height 2.5 m and breadth 0.5 m?
Given: For the cuboidal shape brick:
length (l1) = 25 cm,
breadth (b1) = 15 cm,
height (h1) = 10 cm
For the cuboidal shape wall:
length (l2) = 6 m,
height (h2) = 2.5 m,
breadth (b2) = 0.5 m
To find: Number of bricks required
Solution:
When all the bricks are arranged to build a wall, the volume of all the bricks is equal to volume of wall.
![]()
i. Volume of a brick = l1 x b1 x h1
= 25 x 15 x 10 cc
ii. l2 = 6m = 6 x 100 …[∵ 1m = 100cm]
= 600 cm
h2 = 2.5 m = 2.5 x 100 = 250 cm
b2 = 0.5 m = 0.5 x 100 = 50 cm
Volume of the wall = l2 x b2 x h2
= 600 x 50 x 250 cc
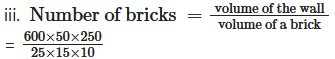
= 40 x 2 x 25
= 2000 bricks
∴ 2000 bricks are required to build the wall.
Question 4.
For rain water harvesting a tank of length 10 m, breadth 6 m and depth 3 m is built. What is the capacity of the tank? How many litre of water can it hold?
Given: For a cuboidal tank,
Length (l) = 10 m, breadth (b) = 6 m, depth (h) = 3 m
To find: Capacity of the tank and litre of water tank can hold.
Solution:
i. l = 10m = 10 x 100 …[∵ 1m = 100cm]
= 1000 cm,
b = 6 m = 6 x 100 = 600 cm,
h = 3 m = 3 x 100 = 300 cm
Volume of the tank = l x b x h
= 1000 x 600 x 300
= 18,00,00,000 cc
ii. Capacity of the tank = Volume of the tank
= 18,00,00,000 cc
![]()
…[∵ 1 litre =1000 cc]
= 1,80,000 litre
∴ The capacity of the tank is 18,00,00,000 cc and it can hold 1,80,000 litre of water.