Chapter 17 Circle: Chord and Arc Set 17.2
Question 1.
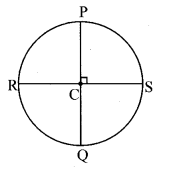
The diameters PQ and RS of the circle with centre C are perpendicular to each other at C. State, why arc PS and arc SQ are congruent. Write the other arcs which are congruent to arc PS.
Solution:
diameter PQ ⊥ diameter RS … [Given]
∴ m∠PCS = m∠SCQ = m∠PCR = m∠RCQ = 90°
The measure of the angle subtended at the centre by an arc is the measure of the arc.
∴ m(arc PS) = m∠PCS = 90° …(i)
m (arc SQ) = m∠SCQ = 90° …(ii)
∴ m(arc PS) = m(arc SQ) … [From (i) and (ii)]
∴ arc PS ≅ arc SQ … [If the measures of two arcs of a circle are same, then the two arcs are congruent]
m(arc PR) = m∠PCR = 90° .. .(iii)
m (arc RQ) = m∠RCQ = 90° … (iv)
∴ m(arc PS) = m(arc PR) = m(arc RQ) … [From (i), (iii) and (iv)]
∴ arc PS ≅ arc PR ≅ arc RQ
… [If the measures of two arcs of a circle are same, then the two arcs are congruent]
∴ arc PR and arc RQ are congruent to arc PS.
Question 2.
In the given figure, O is the centre of the circle whose diameter is MN. Measures of some central angles are given in the figure.
i. m∠AOB and m∠COD
ii. Show that arc AB ≅ arc CD
iii. Show that chord AB ≅ chord CD

Solution:
i. Seg MN is the diameter of the circle. … [Given]
∴ m∠AOM + m∠AON = 180° … [Angles in a linear pair]
∴ m∠AOM + (m∠AOB + m∠BON) = 180° … [Angle addition property]
∴ 100° + m∠AOB + 35° = 180°
…[∵ m∠AOM = 100°, m∠BON = 35°]
∴ m∠AOB + 135° = 180°
∴ m∠AOB = 180°- 135°
∴m∠AOB = 45° …(i)
Also, m∠DOM + m∠DON = 180° … [Angles in a linear pair]
∴ m∠DOM + (m∠COD + m∠CON) = 180° … [Angle addition property]
∴ 100° +m∠COD + 35°= 180°
…[∵ m∠DOM = 100°, m∠CON = 35° ]
∴ m∠COD + 135° = 180°
∴ m∠COD = 180°- 135°
∴ m∠COD = 45° …(ii)
ii. m(arc AB) = m∠AOB = 45° … [From (i)]
m(arc DC) = m∠DOC = 45° .. .[From (ii)]
∴ m(arc AB) = m(arc DC) …[From (i) and (ii)]
∴ arc AB ≅ arc CD
… [If the measures of two arcs of a circle are same, then the two arcs are congruent]
iii. arc AB ≅ arc CD
∴ chord AB ≅ chord CD ….[The chords corresponding to congruent arcs are congruent]
Intext Questions and Activities
Question 1.
If the measures of two arcs of a circle are same, then two arcs are congruent. Verify this property using tracing paper. (Textbook pg. no. 117)
Solution:
[Students should attempt the above activities on their own.]
Question 2.
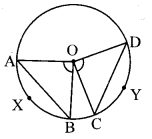
With the help of following activity find out the properties of the chord and the corresponding arc.
i. a. Draw a circle with centre O.
b. Draw ∠COD and ∠AOB of same measure.
You will find that the arc AXB and arc CYD are congruent.
c. Draw chords AB and CD.
d. Using compass experience that the length of chord AB and chord CD is also same.
(Textbook pg. no. 117)
Solution:
[Students should attempt the above activities on their own.]
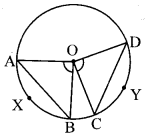
ii. a. Draw a circle with centre C.
b. Draw the congruent chords AB and DE of the circle. Draw the radii CA, CB, CD and CE.
c. Check that ∠ACB and ∠DCE are congruent.
d. Hence show that measure of arc AB and arc DE is equal. Hence these arcs are congruent. (Textbook pg. no. 117)
Solution:
[Students should attempt the above activities on their own.]