Chapter 2 Applications of Derivatives Ex 2.3
Chapter 2 Applications of Derivatives Ex 2.3
Question 1.
Check the validity of the Rolle’s theorem for the following functions.
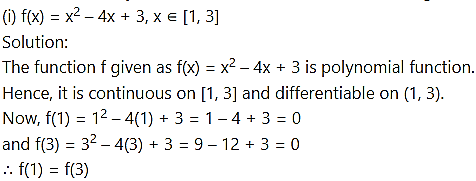
Thus, the function f satisfies all the conditions of Rolle’s theorem.


Hence, the conditions of Rolle’s theorem are not satisfied.
(iv) f(x) = sin x – cos x + 3, x ∈ [0, 2π].
Solution:
The functions sin x, cos x and 3 are continuous and differentiable on their domains.
∴ f(x) = sin x – cos x + 3 is continuous on [0, 2π] and differentiable on (0, 2π).
Now, f(0) = sin 0 – cos 0 + 3 = 0 – 1 + 3 = 2
and f(2π) = sin 2π – cos 2π + 3 = 0 – 1 + 3 = 2
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
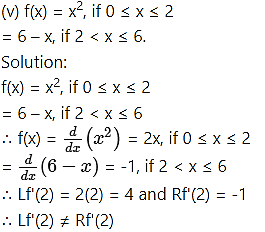
∴ f is not differentiable at x = 2 and 2 ∈ (0, 6).
∴ f is not differentiable at all the points on (0, 6).
Hence, the conditions of Rolle’s theorem are not satisfied.
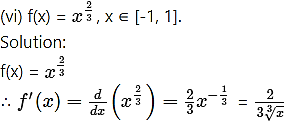
This does not exist at x = 0 and 0 ∈ (-1, 1)
∴ f is not differentiable on the interval (-1, 1).
Hence, the conditions of Rolle’s theorem are not satisfied.
Question 2.

Since, b = 1 satisfies this equation, b = 1 is one of the roots of this equation.
Hence, b = 1.
Question 3.
Verify Rolle’s theorem for the following functions.
(i) f(x) = sin x + cos x + 7, x ∈ [0, 2π]
Solution:
The functions sin x, cos x and 7 are continuous and differentiable on their domains.
∴ f(x) = sin x + cos x + 7 is continuous on [0, 2π] and differentiable on (0, 2π)
Now, f(0) = sin 0 + cos 0 + 7 = 0 + 1 + 7 = 8
and f(2π) = sin 2π + cos 2π + 7 = 0 + 1 + 7 = 8
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
∴ there exists c ∈ (0, 2π) such that f'(c) = 0.
Now, f(x) = sin x + cos x + 7
∴ f'(x) = d/dx (sin x + cos x + 7)
= cos x – sin x + 0
= cos x – sin x
∴ f'(c) = cos c – sin c
∴ f'(c) = 0 gives, cos c – sin c = 0
∴ cos c = sin c
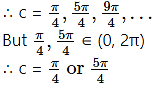
Hence, the Rolle’s theorem is verified.

Now, f(0) = sin 0 = 0
and f(2π) = sin π = 0
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
∴ there exists c ∈ (0, 2π) such that f'(c) = 0.
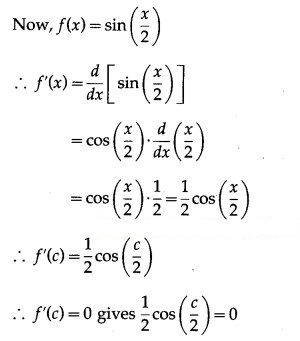
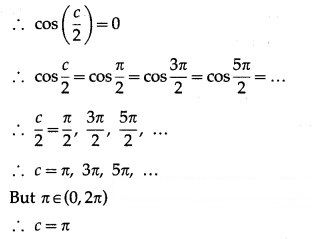
Hence, Rolle’s theorem is verified.
(iii) f(x) = – 5x + 9, x ∈ [1, 4].
Solution:
The function f given as f(x) = – 5x + 9 is a polynomial function.
Hence it is continuous on [1, 4] and differentiable on (1, 4).
Now, f(1) = – 5(1) + 9 = 1 – 5 + 9 = 5
and f(4) = – 5(4) + 9 = 16 – 20+ 9 = 5
∴ f(1) = f(4)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
∴ there exists c ∈ (1, 4) such that f'(c) = 0.
Now, f(x) = x2 – 5x + 9
∴ f'(x) = d/dx ( – 5x + 9)
= 2x – 5 × 1 + 0
= 2x – 5
∴ f'(c) = 2c – 5
∴ f'(c) = 0 gives, 2c – 5 = 0
∴ c = 5/2 ∈ (1, 4)
Hence, the Rolle’s theorem is verified.
Question 4.

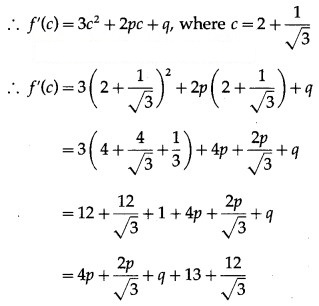
But f'(c) = 0
![]()
∴ (4√3 + 2)p + √3q + (13√3 + 12) = 0
∴ (4√3 + 2)p + √3q = -13√3 – 12 ……. (2)
Multiplying equation (1) by √3, we get
4√3p + √3q= -13√3
Subtracting this equation from (2), we get
2p = -12 ⇒ p= -6
∴ from (1), 4(-6) + q = -13 ⇒ q = 11
Hence, p = -6 and q = 11.
Question 5.
If Rolle’s theorem holds for the function f(x) = (x – 2) log x, x ∈ [1, 2], show that the equation x log x = 2 – x is satisfied by at least one value of x in (1, 2).
Solution:
The Rolle’s theorem holds for the function f(x) = (x – 2) log x, x ∈ [1, 2].
∴ there exists at least one real number c ∈ (1, 2) such that f'(c) = 0.
Now, f(x) = (x – 2) log x
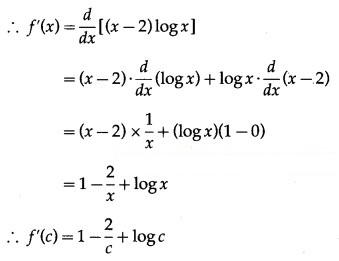
∴ f'(c) = 0 gives 1 – + log c = 0
∴ c – 2 + c log c = 0
∴ c log c = 2 – c, where c ∈ (1, 2)
∴ c satisfies the equation x log x = 2 – x, c ∈ (1, 2).
Hence, the equation x log x = 2 – x is satisfied by at least one value of x in (1, 2).
Question 6.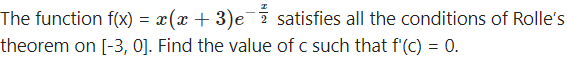
Solution:
The function f(x) satisfies all the conditions of Rolle’s theorem, therefore there exist c ∈ (-3, 0) such that f'(c) = 0.
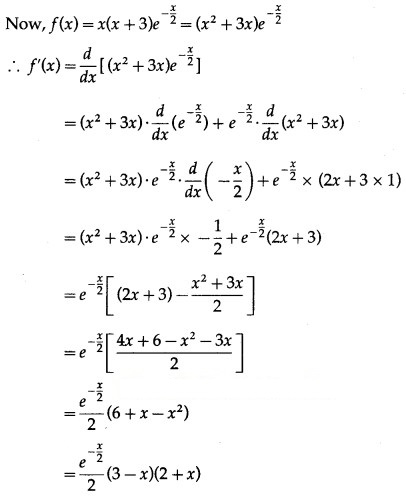
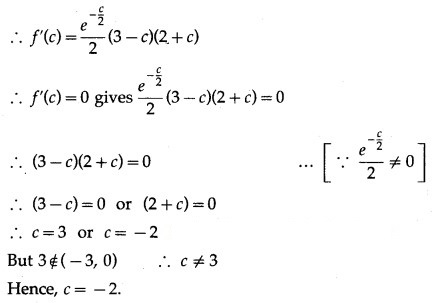
Question 7.
Verify Lagrange’s mean value theorem for the following functions:
(i) f(x) = log x on [1, e].
Solution:
The function f given as f(x) = log x is a logarithmic function that is continuous for all positive real numbers.
Hence, it is continuous on [1, e] and differentiable on (1, e).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (1, e) such that
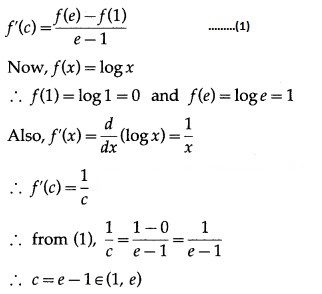
Hence, Lagrange’s mean value theorem is verified.
(ii) f(x) = (x – 1)(x – 2)(x – 3) on [0, 4].
Solution:
The function f given as
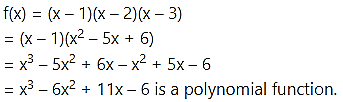
Hence, it is continuous on [0, 4] and differentiable on (0, 4).
Thus, the function f satisfies the conditions of Lagrange’s, mean value theorem.
∴ there exists c ∈ (0, 4) such that
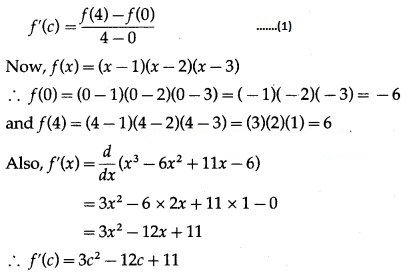
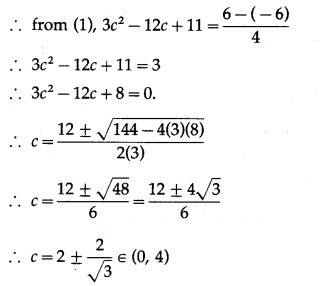
Hence, Lagrange’s mean value theorem is verified.
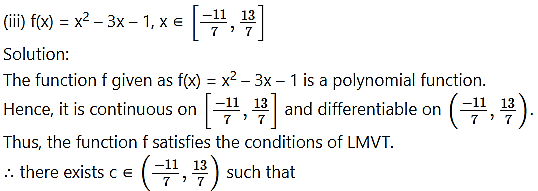
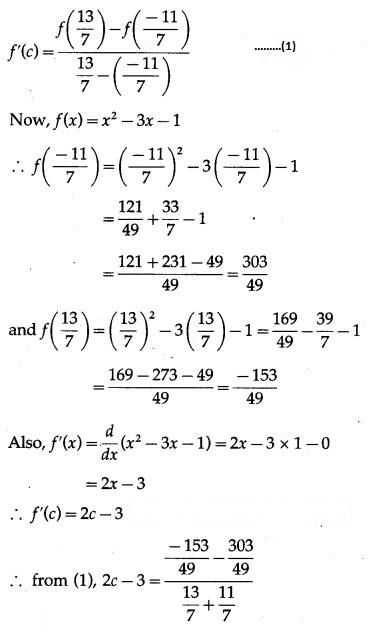
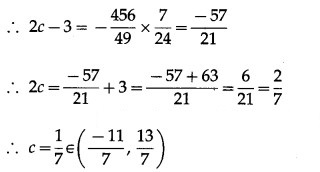
Hence, Lagrange’s mean value theorem is verified.
(iv) f(x) = 2x – , x ∈ [0, 1].
Solution:
The function f given as f(x) = 2x – is a polynomial function.
Hence, it is continuous on [0, 1] and differentiable on (0, 1).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (0, 1) such that
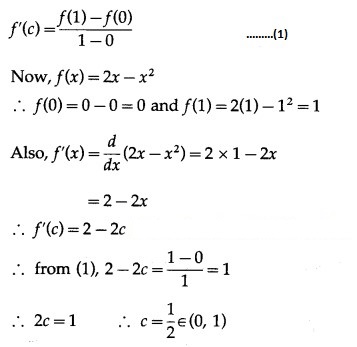
Hence, Lagrange’s mean value theorem is verified.

But 3 ∉ [4, 5]
Hence, it is continuous on [4, 5] and differentiable on (4, 5).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (4, 5) such that
![]()
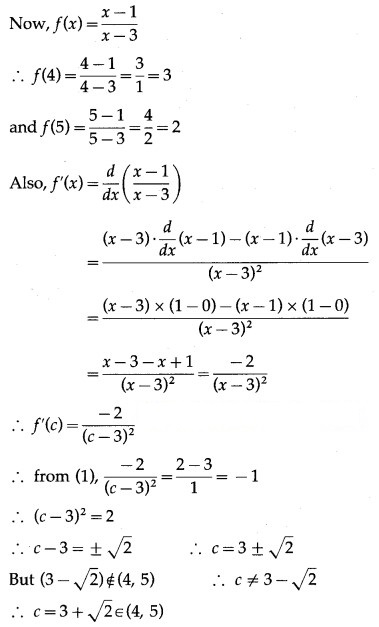
Hence, Lagrange’s mean value theorem is verified.