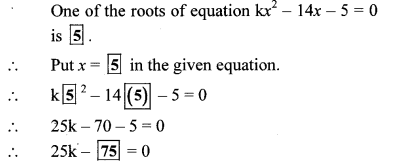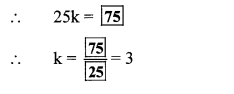Blog

Chapter 2 Quadratic Equations Set 2.1

Chapter 2 Quadratic Equations Set 2.1

Question 1.
Write any two quadratic equations.
Solution:
i. y² – 7y + 12 = 0
ii. x² – 8 = 0

Question 2.
Decide which of the following are quadratic
i. x² – 7y + 2 = 0
ii. y² = 5y – 10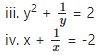

v. (m + 2) (m – 5) = 03
vi. m³ + 3m² – 2 = 3m³
Solution:
i. The given equation is x² + 5x – 2 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 5, c = -2 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

ii. The given equation is
y² = 5y – 10
∴ y² – 5y + 10 = 0
Here, y is the only variable and maximum index of the variable is 2.
a = 1, b = -5, c = 10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

iii. The given equation is
y² += 2
∴ y³ + 1 = 2y …[Multiplying both sides by y]
∴ y³ – 2y + 1 = 0
Here, y is the only variable and maximum index of the variable is not 2.
∴ The given equation is not a quadratic equation.

iv. The given equation is
x +  = -2
∴ x² + 1 = -2x …[Multiplying both sides by x]
∴ x² + 2x+ 1 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 2, c = 1 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

v. The given equation is
(m + 2) (m – 5) = 0
∴ m(m – 5) + 2(m – 5) = 0
∴ m² – 5m + 2m – 10 = 0
∴ m² – 3m – 10 = 0
Here, m is the only variable and maximum index of the variable is 2.
a = 1, b = -3, c = -10 are real numbers and a ≠ 0.
∴ The given equation is a quadratic equation.

vi. The given equation is
m³ + 3m² – 2 = 3m³
∴ 3m³ – m³ – 3m² + 2 = 0
∴ 2m³ – 3m² + 2 = 0
Here, m is the only variable and maximum
index of the variable is not 2.
∴ The given equation is not a quadratic equation.

Question 3.
Write the following equations in the form ax² + bx + c = 0, then write the values of a, b, c for each equation.
i. 2y = 10 – y²
ii. (x – 1)² = 2x + 3
iii. x² + 5x = – (3 – x)
iv. 3m² = 2m² – 9
v. P (3 + 6p) = – 5
vi. x² – 9 = 13
Solution:
i. 2y – 10 – y²
∴ y² + 2y – 10 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = 2, c = -10

ii. (x – 1)² = 2x + 3
∴ x² – 2x + 12x + 3
x² – 2x + 1 – 2x – 30
∴ x² – 4x – 2 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = -4, c = -2

iii. x² + 5x = – (3 – x)
∴ x² + 5x = -3 + x
∴ x² + 5x – x + 3 = 0
∴ x² + 4x + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 4, c = 3

iv. 3m² = 2m² – 9
∴ 3m² – 2m² + 9 = 0
∴ m² + 9 = 0
∴ m² + 0m + 9 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 1, b = 0, c = 9

v. p (3 + 6p) = – 5
∴ 3p + 6p² = -5
∴ 6p² + 3p + 5 = 0
Comparing the above equation with
ap² + bp + c = 0, we get
a = 6, b = 3, c = 5

vi. x² – 9 = 13
∴ x² – 9 – 13 = 0
∴ x² – 22 = 0
∴ x² + 0x – 22 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 0, c = -22

Question 4.
Determine whether the values given against each of the quadratic equation are the roots of the equation.

Solution:
i. The given equation is
x² + 4x – 5 = 0 …(i)
Putting x = 1 in L.H.S. of equation (i), we get
L.H.S. = (1)² + 4(1) – 5 = 1 + 4 – 5 = 0
∴ L.H.S. = R.H.S.
∴ x = 1 is the root of the given quadratic equation.
Putting x = -1 in L.H.S. of equation (i), we get
L.H.S. = (-1)² + 4(-1) – 5 = 1 – 4 – 5 = -8
∴ LH.S. ≠ R.H.S.
∴ x = -1 ¡s not the root of the given quadratic equation.

ii. The given equation is
2m² – 5m = 0 …(i)
Putting m = 2 in L.H.S. of equation (i), we get
L.H.S. = 2(2)² – 5(2) = 2(4) -10 = 8 – 10 = -2
∴ L.H.S. ≠ R.H.S.
∴ m = 2 is not the root of the given quadratic equation.
Putting m = 52 in L.H.S. of equation (i), we get

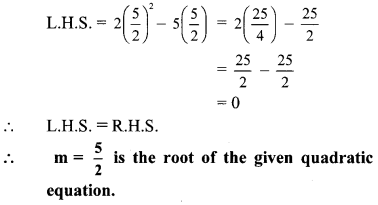
Question 5.
Find k if x = 3 is a root of equation kx² – 10x + 3 = 0.
Solution:
x = 3 is the root of the equation kx² – 10x + 3 = 0.
Putting x = 3 in the given equation, we get
k(3)² – 10(3) + 3 = 0
∴ 9k – 30 +3 = 0
∴ 9k – 27 = 0
∴ 9k = 27
∴ k = 279
∴ k = 3

Question 6.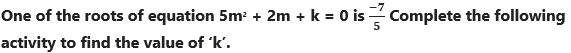

Solution:

Question 1.
x² + 3x – 5, 3x² – 5x, 5x²; Write the polynomials In the index form. Observe the coefficients and fill in the boxes. (Textbook p. no. 31)
Answer:
Index form of the given polynomials:
x² + 3x – 5, 3x² – 5x + 0, 5x² + 0x + 0
i. Coefficients of x2 are [1], [3] and [5] respectively, and these coefficients are non zero.
ii. Coefficients of x are 3, [-5] and [0] respectively.
iii. Constant terms are [-5], [0] and [0] respectively.
Here, constant terms of second and third polynomial is zero.

Question 2.
Complete the following table (Textbook p. no. 31)

Answer:

Question 3.
Decide which of the following are quadratic equations? (Textbook pg. no. 31)
i. 9y² + 5 = 0
ii. m³ – 5m² + 4 = 0
iii. (l + 2)(l – 5) = 0
Solution:
i. In the equation 9y² + 5 = 0, [y] is the only variable and maximum index of the variable is [2].
∴ It [is] a quadratic equation.

ii. In the equation m³ – 5m² + 4 = 0, [m] is the only variable and maximum index of the variable is not 2.
∴ It [is not] a quadratic equation.

iii. (l + 2)(l – 5) = 0
∴ l(l – 5) + 2(l – 5) = 0
∴ l² – 5l + 2l – 10 = 0
∴ l² – 3l – 10 = 0.
In this equation [l] is the only variable and maximum index of the variable is [2]
∴ it [is] a quadratic equation.

Question 4.
If x = 5 is a root of equation kx² – 14x – 5 = 0, then find the value of k by completing the following activity. (Textbook pg, no. 33)
Solution: